隠れマルコフモデル(Hidden Markov Model; HMM)

投稿テストォ…（小声）

まえがき

隠れマルコフモデル(Hidden Markov Model; HMM)は，機械学習の分野から見ると一種の生成モデル ^1 （確率分布を用いて表現されたモデル）であり，次の節に挙げるように著名な応用例があり，重要なモデルであると言える．ここでは，HMMの学習法や，推論動作について述べる.

まずは，HMM動作時の様子を図\ref{fig:HMMDesc}に示す.

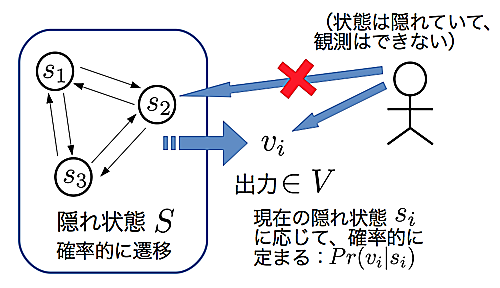HMM動作時の概要図

HMMは観測可能な記号(Symbol)の出力と，観測不可能な隠れ状態(Hidden State)からなる．隠れ状態の遷移確率は，直前の状態に依存する性質（マルコフ性）があり，かつ，記号の出力確率は現在の隠れ状態に依存する．HMMを連続に動作させて次々に出力記号を観測すると，隠れ状態は観測できない一方，出力記号は隠れ状態に依存していることから，その観測記号列は（隠れ状態に依存した）ある隔たりを生じることになる．

従って，観測記号列こそがHMMのパラメタ（ここでは，状態数，隠れ状態の遷移確率，記号の出力確率）を推定するヒントになり，学習におけるサンプルとなる．提示されたサンプルを出力できるようなパラメタは，どの様に設定すれば良いのだろうか．これは手作業で探っていくのは現実的ではないし，第一その設定が妥当だと言える証拠はない.そこで統計学の出番である．統計学における最尤推定法は，非常に大雑把に言って，与えられたサンプル（標本）に最も合うようにパラメタを調整する手法 ^2 である．最尤推定法は生成モデルの学習の論拠となる重大な理論であり，HMMでも最尤推定法は適用され，アルゴリズムに従って，最もサンプルに合ったパラメタを推定することができる．

応用例

隠れマルコフモデルは商業的にも広く使われている.

音声認識

一番有名かつ成功した応用例と言える．発話者の音声 ^3 を観測した結果から，隠れ状態に相当する音素 ^4 の遷移を推定することで実現される．1976年から使用され始め，歴史も有る．近年は深層学習（Deep Learning）に精度面で凌駕されている[^5]．

形態素解析

形態素とは，言語の意味を持つ最小単位の事を言う（トークンと言い換えても問題は無いはず…である）．そして，形態素解析は言語処理において最も基本的かつ重要なタスク（トークン的な喩えをするならば，コンパイラにおける字句解析）である．英語等の単語境界が明快な言語は異なり，日本語は形態素の文字境界が曖昧 ^6 なので形態素解析は一般に難しいと言える．HMMで実現するには，観測するのは形態素候補，隠れ状態には品詞情報を与える．こちらも，昔はHMMがよく使われていたが，現在はCRF[^7]と呼ばれるより表現力の高い確率モデルに押されている．

隠れマルコフモデルの学習や推論

モデルのシンタックス

モデルの形式化を行う．ここで，$c_{2}$が成立している条件下で，$c_{1}$が成立する条件付き確率を$Pr(c_{1}|c_{2})$と表す．

補遺

• $|S| = N_{s}，|V| = N_{o}$とし，$S，V$の要素はインデックスを付けて示す: $$\begin{eqnarray} S &=& \{ s_{1}，s_{2}，\dots，s_{N_{s}} \} \\ V &=& \{ v_{1}，v_{2}，\dots，v_{N_{o}} \}\end{eqnarray}$$

• 遷移確率行列$A$は$N_{s} \times N_{s}$の行列であり，$A$の$(i,j)$成分$(A)_{ij}$は時刻の更新を伴いながら$s_{i}$から$s_{j}$へ遷移する確率である．
  条件付き確率を用いて次の様に表される: $$\begin{eqnarray}
  (A)_{ij} = Pr(\text{時刻}t+1\text{において状態}s_{j}|\text{時刻}t\text{において状態}s_{i})\end{eqnarray}$$

• 観測確率行列$B$は$N_{s} \times N_{o}$の行列であり，$B$の$(i,j)$成分$(B)_{ij}$はある時刻において$s_{i}$にいる時にシンボル$v_{j}$を観測する確率である.
  条件付き確率を用いて次の様に表される: $$\begin{eqnarray}
  (B)_{ij} = Pr(\text{時刻}t\text{において}v_{j}\text{を観測}|\text{時刻}t\text{において状態}s_{i})\end{eqnarray}$$

• $\pi$は，$\pi_{i}$で$s_{i}\ (i = 1,\dots,N_{s})$が初期状態となる確率を表す.

観測列の生成

定義に従って，HMMの動作を改めて記述すると以下の様になる．ここで，時刻$t$における状態の実現値を$q_{t}$，観測の実現値を$O_{t}$とする.

1. 初期状態分布$\pi$に基づき，初期状態$q_{1}$を決定する.
2. $t = 1$とする.
3. 時刻$t$における観測$O_{t}$を，$q_{t}$の観測確率分布に従って決定する.
4. $q_{t}$における遷移確率行列に従って，次の状態$q_{t+1}$を決定する.
5. $t$を増やし，3.に戻るか，$t = T$ならば停止する．

この動作を図示すると図\ref{fig:HMMTre}の様になる ^9 ．この図において，横軸は時刻を表し，各時刻における状態遷移と観測が図示されている．

実際の動作は，$q_{1}$から遷移を辿るパスとなり，状態列$Q = (q_{1},\dots,q_{T})$と観測列$O=(O_{1},\dots,O_{T})$が得られる．

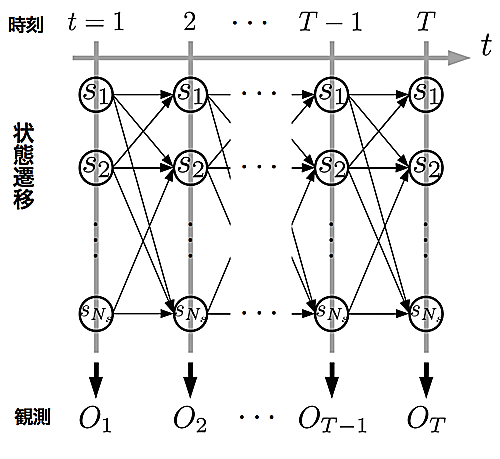HMMのもう少し厳密な動作図

観測列生成確率の効率的計算 : 前向き・後ろ向きアルゴリズム

前節で見た様に，図\ref{fig:HMMTre}のパスを辿ることによって状態列$Q = (q_{1},\dots,q_{T})$と観測列$O=(O_{1},\dots,O_{T})$とが生成される.そこでまず，現在のパラメタにおける，$Q,O$となる列が得られる確率$Pr(Q,O|H)$を計算することを考える．

$t=1$から$t=T$までのパスを見ていくことにより，$Pr(Q,O|H)$は以下の様に計算できる: $$\begin{eqnarray} \label{eq:jointP} \tag{1} Pr(Q,O|H) &=& Pr(q_{1}|q_{0}) Pr(O_{1}|q_{1}) Pr(q_{2}|q_{1}) Pr(O_{2}|q_{2}) \dots Pr(q_{T}|q_{T-1}) Pr(O_{T}|q_{T}) \nonumber \\ &=& \prod_{t=1}^{T} Pr(q_{t}|q_{t-1}) Pr(O_{t}|q_{t}) \end{eqnarray}$$ここで，$Pr(q_{1}|q_{0})$は初期状態分布$\pi$により決定できるので，表記の一貫性保持のために以下この記法を用いる.ここから求めたい観測列の生成確率$Pr(O|H)$を得るには，(\ref{eq:jointP}式)の状態$q_{t}\ (t=1,\dots,T)$について和を取れば良い（周辺化）:
$$\begin{eqnarray} \label{eq:margiO} \tag{2} Pr(O|H) &=& \sum_{q_{1} \in S} \sum_{q_{2} \in S} \dots \sum_{q_{T} \in S} Pr(Q,O|H) \nonumber \\ &=& \sum_{q_{1} \in S} \sum_{q_{2} \in S} \dots \sum_{q_{T} \in S} \prod_{t=1}^{T} Pr(q_{t}|q_{t-1}) Pr(O_{t}|q_{t}) \nonumber \\ &=& \sum_{q_{1},\dots,q_{T}} \prod_{t=1}^{T} Pr(q_{t}|q_{t-1}) Pr(O_{t}|q_{t}) \ \ (\sum_{q_{t} \in S} \equiv \sum_{q_{t}})\end{eqnarray}$$(\ref{eq:margiO}式)は$t=1,\dots,T$までの$q_{t}$の取りうる全ての状態についての和を取っており，計算量は$O(N_{s}^{T})$となる．これではとても実用に耐えない．，この式を計算する効率的な計算アルゴリズム（前向き・後ろ向きアルゴリズム）が存在する．

その計算は動的計画法に基づいており，(\ref{eq:margiO}式)の変形から導く事ができる: $$\begin{eqnarray} Pr(O|H) &=& \sum_{q_{1},\dots,q_{T}} \prod^{T}_{t=1}Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &=& \sum_{q_{T}} \sum_{q_{1},\dots,q_{T-1}} \prod^{T}_{t=1}Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &\equiv& \sum_{q_{T}} \alpha_{T}(q_{T})\end{eqnarray}$$ここで登場した$\alpha_{t}(q_{t})\ (t=1,\dots,T)$は前向きスコアと呼ばれる．$\alpha_{T}(q_{T})$を展開してみると，$$\begin{eqnarray} \alpha_{T}(q_{T}) &\equiv& \sum_{q_{1},\dots,q_{T-1}} \prod^{T}_{t=1} Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &=& \sum_{q_{T-1}} Pr(q_{T}|q_{T-1}) Pr(O_{T}|q_{T}) \sum_{q_{1},\dots,q_{T-2}} \prod^{T-1}_{t=1} Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &=& \sum_{q_{T-1}} Pr(q_{T}|q_{T-1}) Pr(O_{T}|q_{T}) \alpha_{T-1}(q_{T-1})\end{eqnarray}$$この様にして，再び$\alpha_{T-1}(q_{T-1})$を展開することを繰り返していくと，一般的に前向きスコア$\alpha_{t}(q_{t})\ (t=1,\dots,T)$は次で表せる事が分かる．
$$\begin{eqnarray} \alpha_{t}(q_{t}) = \sum_{q_{t-1}} Pr(q_{t}|q_{t-1}) Pr(O_{t}|q_{t}) \alpha_{t-1}(q_{t-1})\end{eqnarray}$$従って，観測列の生成確率$Pr(O|H)$を計算するには，$\alpha_{t}(q_{t})$を$t=1$から始めて（$\alpha_{0}(q_{0}) = 1$とする）$t=T$まで計算し，最後に$q_{T} \in S$についての和を取れば良いことになる．

この手順に従った計算アルゴリズムを前向きアルゴリズムと呼ぶ．，計算量は$O(TN_{s}^{2})$まで改善される．また，前向きスコア$\alpha_{t}(q_{t})$は，時刻$t$での状態が$q_{t}$かつ，時刻$1,\dots,t$での出力ラベルが$O_{1},\dots,O_{t}$となる確率を表していることも重要な事実である．
，前向きアルゴリズムとは逆（$t=T$から初めて$t=1$まで）の方向で観測列の生成確率を計算する事もできる．

再び$Pr(O|H)$を変形すると，$$\begin{eqnarray} Pr(O|H) &=& \sum_{q_{1},\dots,q_{T}} \prod^{T}_{t=1}Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &=& \sum_{q_{1}} Pr(q_{1}|q_{0}) Pr(O_{1}|q_{1}) \sum_{q_{2},\dots,q_{T}} \prod^{T}_{t=2}Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &\equiv& \sum_{q_{1}} \beta_{1}(q_{1})\end{eqnarray}$$$\beta_{t}(q_{t})\ (t=1,\dots,T)$を後ろ向きスコアと呼ぶ．$\beta_{1}(q_{1})$を展開すると，$$\begin{eqnarray} \beta_{1}(q_{1}) &\equiv& \sum_{q_{2},\dots,q_{T}} \prod^{T}_{t=2} Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &=& \sum_{q_{2}} Pr(q_{2}|q_{1}) Pr(O_{2}|q_{2}) \sum_{q_{3},\dots,q_{T}} \prod^{T}_{t=3}Pr(q_{t}|q_{t-1})Pr(O_{t}|q_{t}) \\ &=& \sum_{q_{2}} Pr(q_{2}|q_{1}) Pr(O_{2}|q_{2}) \beta_{2}(q_{2})\end{eqnarray}$$前向きアルゴリズムの時と同様にして，$\beta_{t}(q_{t})$は $$\begin{eqnarray} \beta_{t}(q_{t}) = \sum_{q_{t+1}} Pr(q_{t+1}|q_{t}) Pr(O_{t+1}|q_{t+1}) \beta_{t+1}(q_{t+1})\end{eqnarray}$$を満たす事がわかる．$Pr(O|H)$の計算には，$\beta_{t}(q_{t})$を$t=T$から始めて（$\beta_{T}(q_{T}) = 1$とする）$t=1$まで計算し，最後に$q_{1} \in S$についての和を取れば良い．この手順を後ろ向きアルゴリズムと呼ぶ．

そして後ろ向きスコア$\beta_{t}(q_{t})$は時刻$t$において状態が$q_{t}$である時，その後の出力系列が$O_{t+1},\dots,O_{T}$となっている確率を表している事が，前向きスコアの時と同様重要である．

$Pr(O|H)$の計算については，上記の結果から次の式が成り立つ．
$$\begin{eqnarray} Pr(O|H) &=& \sum_{q_{T}} \alpha_{T}(q_{T}) = \sum_{q_{1}} \beta_{1}(q_{1}) \\ &=& \sum_{q_{t}} \alpha_{t}(q_{t}) \beta_{t}(q_{t}) \ \ (t=1,\dots,T)\end{eqnarray}$$下段の等式の$\alpha_{t}(q_{t}) \beta_{t}(q_{t})$に注目すると，これは全体の観測列は$O$だが，途中の時刻$t$で状態$q_{t}$を通過する確率を表している．

この結果は次節の学習の際に重要な役割を果たす．

HMMの学習 : Baum-Weltchアルゴリズム

一番の関心点：HMMを学習することを考えてみる．学習は概要で述べた通り最尤推定法の考え方に基づく．仮に，隠れ状態の遷移情報がサンプルとして与えられれば，遷移確率$\hat{Pr}(s_{j}|s_{i})$と観測確率$\hat{Pr}(v_{k}|s_{i})$はベイズの定理を用いて次の式（経験確率）で推定できる:
$$\begin{eqnarray} \hat{Pr}(s_{j}|s_{i}) &=& \frac{\hat{Pr}(s_{i},s_{j})}{\hat{Pr}(s_{i})} = \frac{A_{ij}}{\sum_{uv}A_{uv}} \left( \frac{\sum_{u}A_{iu}}{\sum_{uv}A_{uv}} \right)^{-1} = \frac{A_{ij}}{\sum_{u}A_{iu}} \\ \hat{Pr}(v_{k}|s_{i}) &=& \frac{\hat{Pr}(s_{i},v_{k})}{\hat{Pr}(s_{i})} = \frac{B_{ik}}{\sum_{u}B_{iu}}\end{eqnarray}$$ここで$A_{ij}$は状態$s_{i}$から$s_{j}$の遷移が起こった頻度（回数）であり，$B_{ij}$は状態$s_{i}$で$v_{k}$を観測した頻度である．そして各式の分母では，$s_{i}$に入る全ての頻度を足しあわせている．考え方はサイコロのある目が出る確率を経験から求める時と全く同一である．

この式により，最もサンプルに適合した遷移確率と観測確率を計算できるが，実際には状態は観測できないため直接これらの値を計算出来ない．しかしながら，HMMで用いられるBaum-Welch（バウム-ウェルチ）アルゴリズムは，適当な初期状態（遷移確率，観測確率の組）から初め，上式を推定し，推定値を新たな状態として，状態がある値に収束するまで再推定を繰り返すアルゴリズム ^10 である．

まずサンプルの表記から始める．今，サンプルとして観測系列が$M$個与えられたとする: $$\begin{eqnarray} X^{l} = X_{1}^{l},\dots,X_{|X^{l}|}^{l} \ \ l = 1,\dots,M\end{eqnarray}$$サンプルの観測系列の長さは各$l$で異なっても良く，上式において$X^{l}$の長さを$|X^{l}|$と表記している．この時，サンプル$X^{l}$に対する，時刻$t-1$から$t$への状態遷移（$q_{t-1} = s_{i}$かつ$q_{t} = s_{j}$）が発生する確率$\eta_{l}(i,j,t) (= Pr(q_{t-1} = s_{i}，q_{t} = s_{j}|H，X^{l}) )$は次の式で計算できる:
$$\begin{eqnarray} \eta_{l}(i,j,t) = \frac{\alpha_{t-1}(s_{i})Pr(s_{j}|s_{i})Pr(X^{l}_{t}|s_{i})\beta_{t}(s_{j})}{Pr(X^{l}|H)}\end{eqnarray}$$$\eta_{l}(i,j,t)$の分子は観測列が$X^{l}$となる条件下で，$q_{t-1} = s_{i}，q_{t} = s_{j}$となる確率である．$\alpha_{t-1}(s_{i})$によって時刻$t-1$までの観測列が$X_{1}^{l},\dots,X_{t-1}^{l}$かつ，時刻$t-1$において状態が$s_{i}$となる確率を計算でき，また$\beta_{t}(s_{j})$によって状態$s_{j}$から始まって，時刻$t+1$以降の観測系列が$X^{l}_{t+1},\dots,X^{l}_{|X^{l}|}$となる確率を計算できる．

一方$\eta_{l}(i,j,t)$の分母は現在のパラメタにおける$X^{l}$の生成確率 ^11 であり，前向き・後ろ向きアルゴリズムで計算できる（例えば，前向きならば$\sum_{q_{|X^{l}|}}\alpha_{|X^{l}|}(q_{|X^{l}|})$）．よって，分子を分母で割ることで観測列$X^{l}$が与えられた条件下での状態遷移（$q_{t-1} = s_{i}$かつ$q_{t} = s_{j}$）の発生確率$Pr(q_{t-1} = s_{i}，q_{t} = s_{j}|H，X^{l})$が計算できる．ここで，式にある遷移確率や観測確率は現在の推定値を用いれば良い．

そして，状態$s_{i}$から$s_{j}$への遷移が起こる頻度の，サンプル$X^{l}$における推定値$\hat{A}_{ij}^{l}$は，全ての時間での確率を足しあわせた期待値（頻度なので，各確率の重み付けは$1$）で計算できる: $$\begin{eqnarray} \hat{A}_{ij}^{l} = \sum_{t=1}^{|X^{l}|} \eta_{l}(i,j,t)\end{eqnarray}$$この期待値を用いて，遷移確率の更新式が得られる: $$\begin{eqnarray} \hat{Pr}(s_{j}|s_{i}) = \frac{\hat{A}_{ij}^{l}}{\sum_{u}\hat{A}_{iu}^{l}}\end{eqnarray}$$この式を各サンプル$l=1,\dots,M$を与えて逐次計算していき，収束を判定すれば良いことになる．，全てのサンプルを見せて ^12 から期待値を計算（$\sum_{l=1}^{M}\hat{A}^{l}_{ij}$を頻度$\hat{A}_{ij}$とする）しても同様に推定値を計算できる．

この様に，全てのサンプルを見せて一気に学習する手法をバッチ学習（Batch Learning）と呼び，一方ひとつのサンプルを見せながら逐次推定値を計算していく手法をオンライン学習（Online Learning）と呼ぶ．サンプル数$M$が多い場合（特に，ビッグデータ（笑））やメモリ容量の問題があるときにはオンライン学習が適している ^13 ．
．この場合はまず，サンプル$X^{l}$に対する，時刻$t$で状態$s_{i}$にいる確率の推定値$\gamma_{l}(i,t)$を考える:
$$\begin{eqnarray} \gamma_{l}(i,t) = \frac{\alpha_{t}(s_{i})\beta_{t}(s_{i})}{Pr(X^{l}|H)}\end{eqnarray}$$この式の考え方も$\eta_{l}(i,j,t)$と殆ど同じであり，分子において，観測列が$X^{l}$となる条件下で，時刻$t$において状態$s_{i}$にいる確率を計算している．そして観測の期待値$\hat{B}_{ik}$は全ての時間における，時刻$t$における観測$X_{t}^{l}$が$v_{k}$の時の$\gamma_{l}(i,t)$についての和となる:
$$\begin{eqnarray} \hat{B}_{ik} = \sum_{t=1，X_{t}^{l}=v_{k}}^{|X^{l}|} \gamma_{l}(i,t)\end{eqnarray}$$この期待値を用いて，遷移確率の時と同様に観測確率の更新式が得られる: $$\begin{eqnarray} \hat{Pr}(v_{k}|s_{i}) = \frac{\hat{B}_{ik}^{l}}{\sum_{u}\hat{B}_{iu}^{l}}\end{eqnarray}$$上記の議論と同様に，全サンプルに対しても計算することもできる．

HMMの推論 : Viterbiアルゴリズム

仮に今HMMが学習され，次はHMMを推論に用いたいとする．即ち，長さ$T$の観測列$X=X_{1},\dots,X_{T}$を見た時の内部状態の遷移列$\hat{Q}=\hat{q}_{1},\dots,\hat{q}_{T}$を適切に推定したいとする．

適切な列とは，観測列$X$を与える確率が最も高い遷移列であるといえるので，数式で表すと，次の最大化問題を考えることになる: $$\begin{eqnarray} \hat{Q} = \underset{Q}{\rm argmax}\ Pr(Q，X| H)\end{eqnarray}$$Viterbi（ビタビ，ヴィタビ，ビタービなど諸説）アルゴリズムは動的計画法の一種であり，$\hat{Q}$を次の2ステップに分けて求めることができる ^14 :

1． 前向きに最大確率と，その確率を与える直前時刻の状態を記録

2． 末尾から後ろ向きに最大確率を与える状態の記録を辿り，逆順に最適列を求める．

時刻$t$における状態$q_{t} \in S$の最大確率[^15]を$m(q_{t},t)$，また$m(q_{t},t)$を与える直前時刻の状態を$s(q_{t},t)$と表す．

上の第1ステップは，次の様に表すことができる: $$\begin{eqnarray} m(q_{t},t) &=& \left\{ \begin{array}{ll} \pi_{i} Pr(X_{1}|q_{1})\ \ \mathrm{s.t.}\ q_{1} = s_{i} & t = 1 \\ \displaystyle\max_{q_{t-1}} \left[ m(q_{t-1},t-1) Pr(q_{t}|q_{t-1}) Pr(X_{t}|q_{t}) \right] & t = 2,\dots,T \end{array} \right. \\ s(q_{t},t) &=& \underset{q_{t-1}}{\rm argmax} \ \! \! \left[ m(q_{t-1},t-1) Pr(q_{t}|q_{t-1}) Pr(X_{t}|q_{t}) \right] \ \ t = 2,\dots,T\end{eqnarray}$$これを全ての状態$q_{t} \in S$について，$t=1$から$t=T$まで動かせば第1ステップは終了する．

次の第2ステップは簡単で，まず$\hat{q}_{T} = \underset{q_{T}}{\rm argmax} \ m(q_{T},T)$とし，あとはその最大確率を与える系列を$\hat{q}_{t} = s(\hat{q}_{t+1},t+1)$によって，$t=T-1$から$t=1$まで辿れば良い．

またその最大確率値は$\displaystyle\max_{q_{T}} m(q_{T},T)$で求められる．

[^5]: 但し，全てのDeep Learningに言えることだが，学習がとにかく遅い．

[^7]: Conditional Random Field．邦訳で条件付き確率場．元は統計力学の文脈で用いられていたが，現在機械学習の生成モデルの分野において大きな地位を占める．

[^15]: 実装上の注意事項: 確率の積をPCで計算させるとアンダーフローを起こしがちである．その為，確率の対数値をとってから計算し，後で戻す処理がよく行われる．

お兄さん許して！脚注が壊れるわ…（しんみり）