行列の積が覚えられない
この記事の目標
行列の積の定義。慣れるまでは「なんでこんなゴツい定義なんだよ！」とツッコミたくなる形をしています。ここでは行列の積の定義式を覚えなくとも，計算の仕方だけ覚えてしまえる方法を提案します。
とりあえずここでは，数は複素数としてお考え下さい。
長めの数式があります。スマホで閲覧される場合は横向きでにすることを推奨します。
2×2行列のとき
まずは$2\times 2$行列のときの積を考えてみましょう。
$2\times2$行列に対して，次のように行列の積を定義する。$$ \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{bmatrix}\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{bmatrix} \colon\!= \begin{bmatrix} a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\ a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \\ \end{bmatrix} $$
まずはこれに対する覚え方を提案します。こんな図を書いてみましょう。
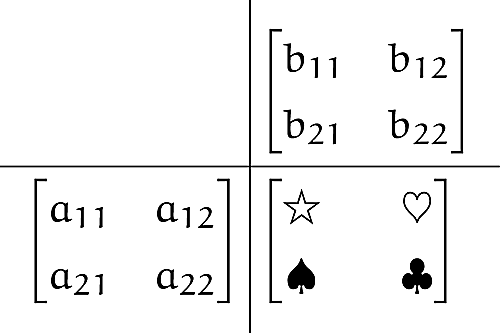2*×2行列の積
つまり，積$AB$を計算したいときに，$A$を左下に，$B$を右上に書いて，その積$AB$を右下に出力したいわけです。例えば定義によれば，$$
\spadesuit=a_{21}b_{11}+a_{22}b_{21}
$$
です。この$\spadesuit$の計算に必要な部分だけ色付けしてみると，以下の画像のようになりますね。
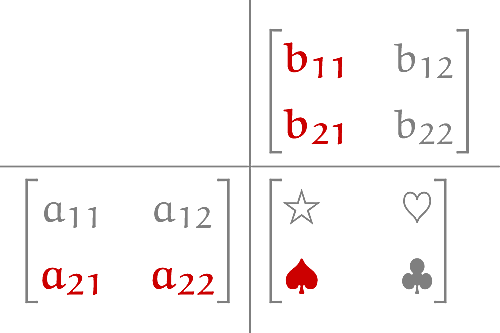横と縦１
特にこれは，$\spadesuit$と同じ列にある2つのベクトル$(a_{21},\,a_{22})$と$(b_{11},\,b_{21})$の内積を取っているとみなせます。他の場合でも同様です。例えば$\clubsuit$ですと，
$$\clubsuit=a_{21}b_{12}+a_{22}b_{22}=(a_{21},\,a_{22})\mdot(b_{12},\,b_{22})$$
となります。なるほど！行列の積は内積を取りまくればよいのか！！
一般の行列へと拡張できるか？
前節で考えた図を用いながら，より一般的な行列の積を計算してみたくなります。
次の積は計算可能か？可能ならば計算せよ。
$$\text{⑴}\quad \begin{bmatrix}
1&2&3\\
4&5&6
\end{bmatrix}\begin{bmatrix}
1&3&4\\
5&6&2\\
2&4&0
\end{bmatrix}$$
$$\text{⑵}\quad \begin{bmatrix} 1&3&4\\ 5&6&2\\ 2&4&0 \end{bmatrix}\begin{bmatrix} 1&2&3\\ 4&5&6 \end{bmatrix}$$
まずは⑴から考えてみます。先ほどの図のように書くならば，以下のようになるはずです。
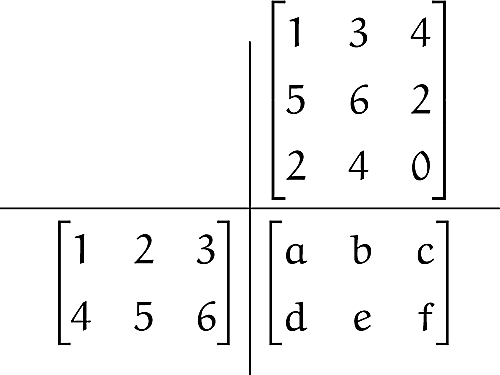横と縦２
例えばこの例ですと，$$
b=1\mdot3+2\mdot6+3\mdot4=27
$$
と計算できます。つまりは3次元ベクトルの内積を取っているものだと解釈できます。他の成分も同様に頑張ることで，$$
\begin{bmatrix}
1&2&3\\
4&5&6
\end{bmatrix}\begin{bmatrix}
1&3&4\\
5&6&2\\
2&4&0
\end{bmatrix}=\begin{bmatrix}
17&27&8\\
41&66&26
\end{bmatrix}
$$
と計算できることが分かります。
では次に，⑵の状況も図で表してみましょう。以下のようになるはずです。
？？？
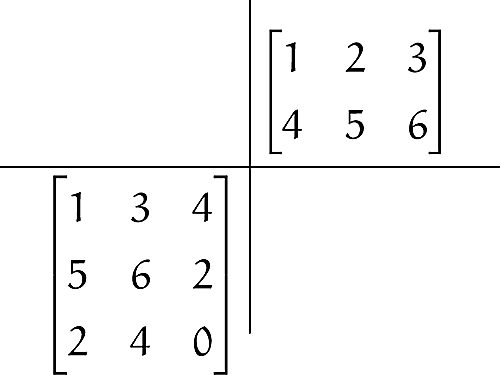さて，これも内積を取ってみたいところですが，いざとってみようとすると，ん？？オカシイナ？？ってなるはずです。
実際に，⑵の場合は積の計算は定義されていません。ということは，今考えている図を使えば，行列の積が定義できるかどうかも判別できるのではないでしょうか！
というわけで一般の行列へ拡張
まずは普通に行列の積を定義します。
$A=(a_{ij})$を$k\times l$行列，$B=(b_{ij})$を$m\times n$行列とする。$\bm{l=m}$の場合のみ積が定義され，$C=AB$として$C=(c_{ij})$とするとき，$c_{ij}$を次のように定める。なお，$C$は$k\times n$行列である。$$ c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots\cdots+a_{im}b_{mj}=\sum_{p=1}^m a_{ip}b_{pj} $$
これを図で表すと，次の状況になります。
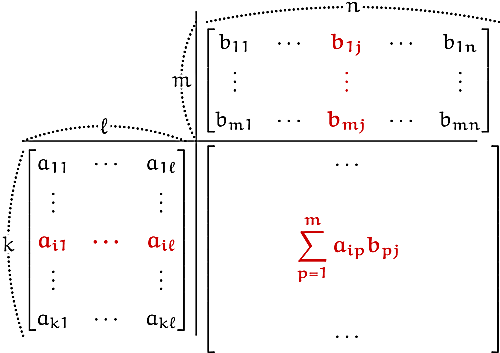一般化
① 積$AB$を計算したいとき，$A$を左下に，$B$を右上に配置する。
② $\bm{\ell=m}$となること，つまり左上が正方形となることが，$AB$が計算可能な条件である。
③ 積$AB$は右下に計算され，$(i,\,j)$成分は，それぞれの$i$行と$j$列のベクトルの内積を取るように計算する。
④ 右下にできた$AB$は，$k\times n$行列である。
このように，図で表すことで，積が計算可能な条件まで幾何的にミエてきます。
まとめ
今回は行列の積を覚えやすくするために，くふうした演算方法を提案しました。特に初学者に教えるときは，非常に重宝する方法ではないかと思っています。ここまでご覧いただきありがとうございました。
宣伝（TeX2img）
今回図示に使ったアプリケーションです。TeXのアウトプットを綺麗に画像化してくれます。
ぜひ使ってみてください！