文献あり

Fano平面の対称性について考える

Fano平面

Steinerシステム

$v$点集合$\Omega=\lbrace\alpha_1,\alpha_2,\cdots,\alpha_v\rbrace$とその部分集合族$\mathcal{B}=\lbrace B_1,B_2,\cdots,B_b\rbrace$の組$(\Omega,\mathcal{B})$であって, 条件

任意の$1\leq i\leq b$に対して, $|B_i|=k$
$\Omega$の任意の$t$元$\alpha_{p_1},\alpha_{p_2},\cdots,\alpha_{p_t}$を取ったとき, $\alpha_{p_1},\alpha_{p_2},\cdots,\alpha_{p_t}\in B_i$となる$B_i\in\mathcal{B}$が存在して一意

を満たすものをSteinerシステムと呼び, $S(t,k,v)=S(\Omega,\mathcal{B})$のように表記する.
$\mathcal{B}$の元をブロックという.

　$S(2,3,7)$をFano平面と呼び, 下の幾何的な表現がよく知られている.

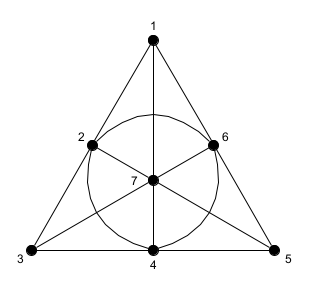Fano平面

どの2点も必ず一つの線(円)に属していることが確認できる. ブロックを列挙すると
\begin{eqnarray} S(2,3,7)=\lbrace(1,2,3),(1,4,7),(1,5,6),(2,4,6)\\ (2,5,7),(3,4,5),(3,6,7)\rbrace \end{eqnarray}
となる.
7次対称群$\mathfrak{S}_7$の元で, ブロックをブロックに移す部分群をFano平面の自己同型群とする. 厳密には以下のように定義される.

$S=S(t,k,v)=S(\Omega,\mathcal{B})$をSteinerシステムとする. $\sigma\in{\rm Sym}\Omega,B\in\mathcal{B}$に対して,
\begin{eqnarray} \sigma B=\lbrace\sigma(\alpha)|\alpha\in B\rbrace \end{eqnarray}
と定める. このとき,
\begin{eqnarray} {\rm Aut}S\coloneqq\lbrace\sigma\in{\rm Sym}\Omega|{}^{\forall}B\in\mathcal{B},\sigma B\in\mathcal{B}\rbrace \end{eqnarray}
は置換群${\rm Sym}\Omega$の部分群であり, $\mathcal{B}$に左から作用する.
このような${\rm Aut}S$を$S$の自己同型群とする.

　以下, $G\coloneqq{\rm Aut}S(2,3,7)$とする.

方針

　Fano平面の対称性について, 次の2つの視点から考察を試みる.

正五胞体への埋込
LeviグラフのHamilton閉路

2については Configurations from a Graphical Viewpoint(p.170-173) を参考にしている.

Fano平面の一部を正四面体に埋め込む

　Fano平面は一見したところ, 直線と円によって構成されているが, 直線も三次元空間では円をなしていると考えれば, 以下のように正四面体へ埋め込むことができる.

Fano平面と正四面体

　ただし, 図2では前面の内接円は省略していて, 点7に関してはすぐに回収する.
図1のFano平面のブロックは$(2,4,6)$のみ円で他は直線と, 表現が統一されていなかったが, 図2ではすべてのブロックが正四面体の面として, すべての点が正四面体の辺として表現できている.

正四面体を正五胞体に埋め込む

　点7を他の点と等価に表現するため, 図2の正四面体を正五胞体へと埋め込む.

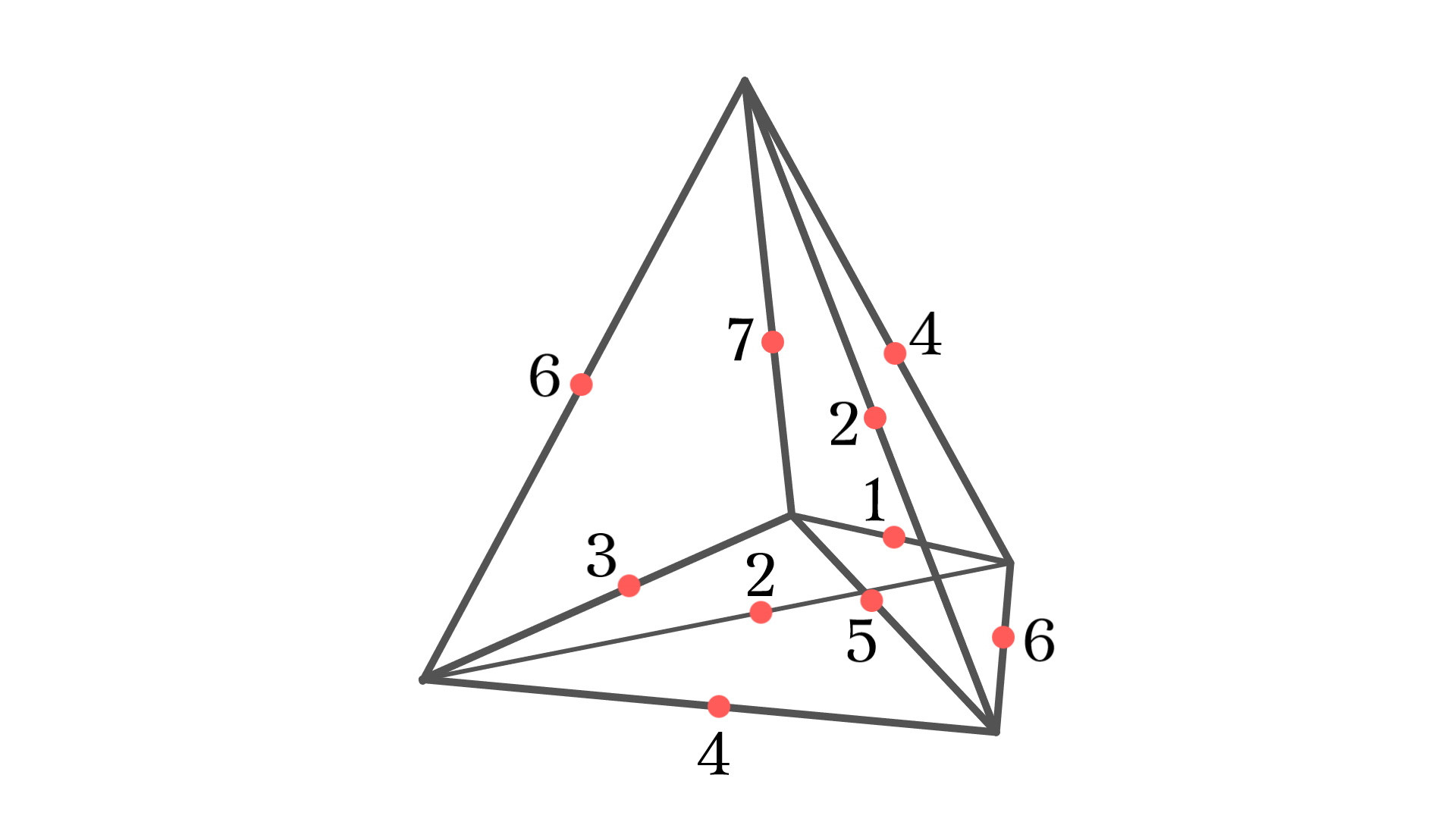Fano平面と正五胞体

　ブロック$(2,4,6)$を表している面が3つ確認できるが, Fano平面としての対称性は崩れていない. 図3から, $G$は4次対称群$\mathfrak{S}_4$を部分群として含むことは一目瞭然である. ただし, この場合の$\mathfrak{S}_4$は正五胞体の辺に対して作用していることに注意. 明示的に共役類の代表元を書き起こすと,
\begin{eqnarray} \lbrace\mqty(1&3&5)\mqty(2&4&6),\mqty(1&5)\mqty(2&4),\mqty(1&3&5&7)\mqty(2&4),\mqty(1&5)\mqty(2&4),\mqty(1)\rbrace \end{eqnarray}
となる.
$\mathfrak{S}_4$として見たときのそれぞれの置換の型は$(3,1),(2,1,1),(4),(2,2),(1,1,1,1)$.

4次元からの視点

　次に図3の内側の正四面体の対称性を考える.
最も理解しやすい操作は2点交換であろう. 例えば$\mqty(1&6)\mqty(2&7)$がそれに当たり, 図3に対して作用させると

!FORMULA[34][-508666964][0]
交換された点を!HTML[0][-1546216315][0]で表している $\mqty(1&6)\mqty(2&7)$
交換された点を青で表している

　ここで注目すべきは外側の面が$(2,4,6)$から$(1,4,7)$に変化しているという点である. ここでも先ほどと同様に$\mathfrak{S}_4$が部分群として得られる. $S(2,3,7)$にはブロックが7個含まれているのだから, 4次元での2点交換と3次元での正四面体の対称群から少なくとも
\begin{eqnarray} 7\cdot4!=168 \end{eqnarray}
通りの操作が得られる.
このことから, 大雑把な$G$の構造が浮かび上がってくる.
7は素数であるから, 外側の面を変化させる操作で位数7の巡回群$C_7$と同じ構造を持っているものが存在しているはずである.
また, $\mathfrak{S}_4=\langle\mqty(1&2),\mqty(2&3&4)\rangle$であり, これらの生成元は正四面体に作用して, 切頂六面体と同型なCayleyグラフを形成する.

!FORMULA[43][852653536][0]のCayleyグラフ
!HTML[1][1420911445][0] : !FORMULA[44][1720082065][0]
!HTML[2][-1727142672][0] : !FORMULA[45][324810017][0] $\mathfrak{S}_4$のCayleyグラフ
赤 : $\mqty(1&2)$
緑 : $\mqty(2&3&4)$

以上を併せて考えれば, $G$のCayleyグラフは次のニュアンスを持つのではないだろうか.

!FORMULA[47][36833][0]のCayleyグラフのイメージ $G$のCayleyグラフのイメージ

Leviグラフからの考察

　三次元空間内での正四面体の操作については構造が明らかになっているが, そこへ4次元の回転を含めると直感的な考察は困難になる. そこで, Fano平面をLeviグラフで表現し, 上の$C_7$(図6の青矢印)周りの構造を決定する.

Leviグラフ

Steinerシステム$S=S(\Omega,\mathcal{B})=S(t,k,v)$のLeviグラフとは, 頂点集合$\Omega\cup\mathcal{B}$と辺集合$E=\lbrace(\alpha,B)|\alpha\in\Omega,B\in\mathcal{B},\alpha\in B\rbrace$のグラフ$L=(\Omega\cup\mathcal{B},E)$である.

Leviグラフの基本的な性質

Steinerシステム$S=S(\Omega,\mathcal{B})=S(t,k,v),|\mathcal{B}|=b$のLeviグラフ$L=(\Omega\cup\mathcal{B},E)$は以下を満たす.

単純な二部グラフで2-彩色可能
頂点の次数は$k$または$b$である
$|\Omega\cup\mathcal{B}|=v+b,|E|=bk=vr$
内周は6以上の偶数である

(内周が6以上の偶数であること)

二部グラフの閉路の長さは偶数であるから, 内周は4または6以上である.
Leviグラフが長さ4の閉路を持つとすると, $\Omega$の2点が異なる2つのブロックに含まれることになるが, これはSteinerシステムの定義に反する.
よって, 内周は6以上である.

　Fano平面のLeviグラフはHeawoodグラフとして知られており, 3-正則のHamiltonグラフである.

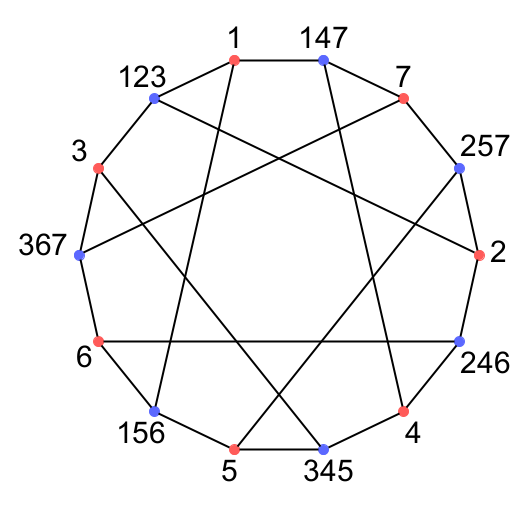Heawoodグラフ
長さ6の閉路を持つ

Heawoodグラフで赤頂点を赤頂点へ, 青頂点を青頂点へ移すような自己同型群$H$を考える. このとき, $G$は$H$の部分群である.
図7のHamilton閉路について考える.
まず, 外周を周る閉路は明らかにHamiltonianである.

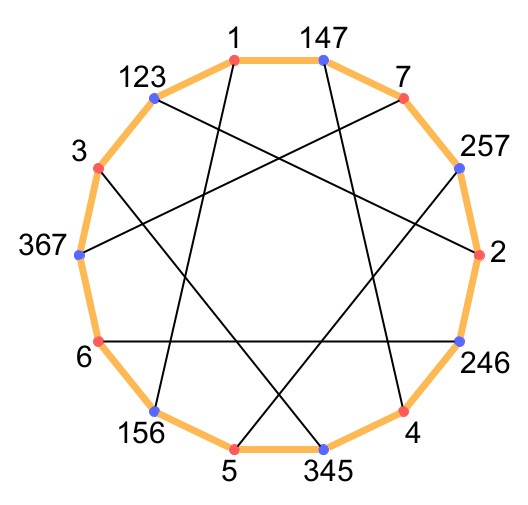外周のHamilton閉路

Heawoodグラフは14角形であるが, 頂点の色を保存するという制約の下では7角形と同じ対称性を持つ. 加えて鏡映反転もできないためその対称性はより低下する.
しかし$C_7$まで落ちるわけではなく, その中間のFrobenius群に落ち着く.

HolomorphとFrobenius群

　ここで手短にHolomorph,Frobenius群,二面体群,巡回群についての説明を挟んでおく. これらはすべて正多角形の回転と変形から生じる群で, 巡回群は回転移動, それに鏡映反転を付加したものが二面体群である.

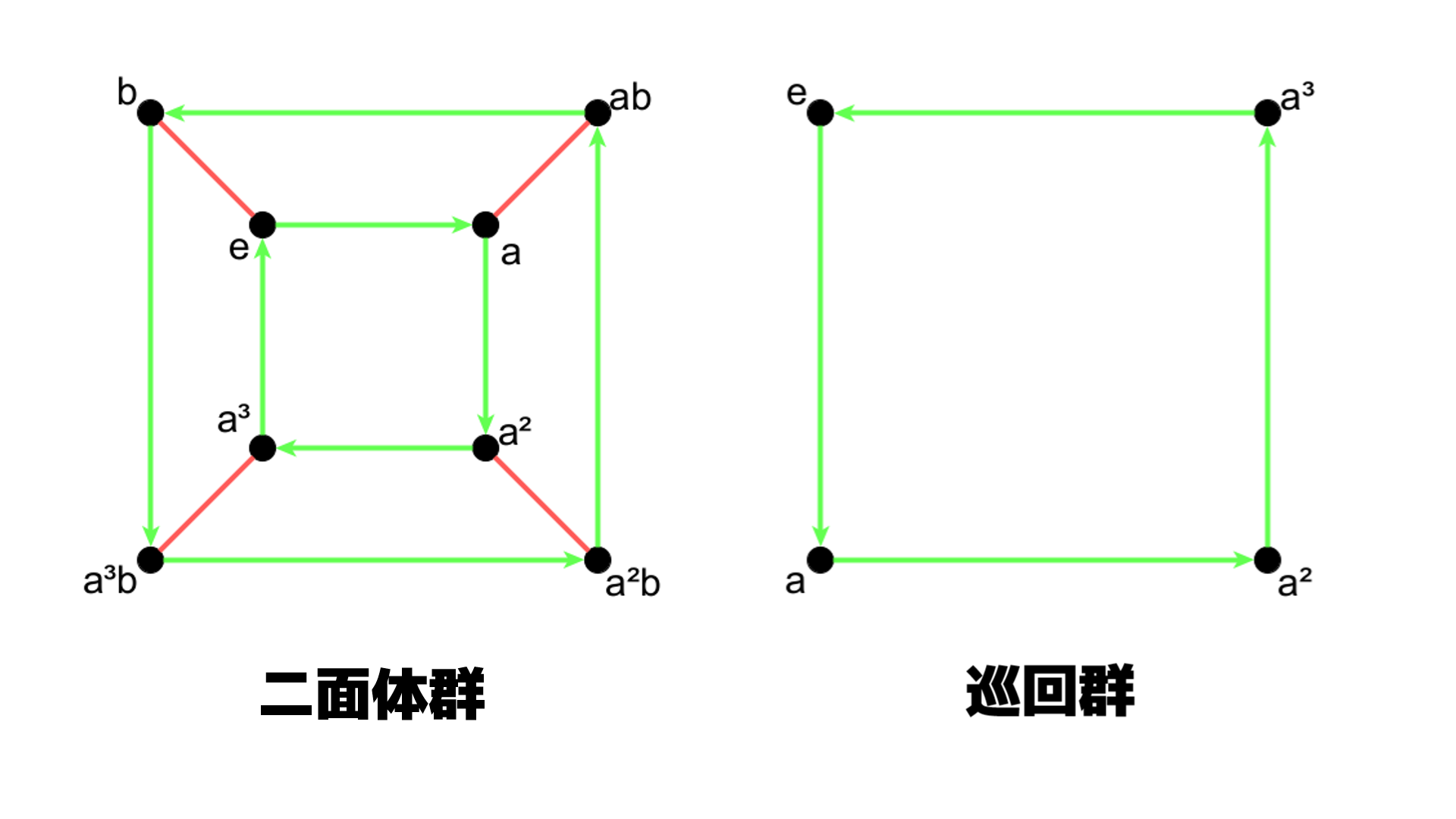二面体群と巡回群のCayleyグラフ

HolomorphとFrobenius群はさらに多角形の変形も許す. 例えば, 五角形では

!FORMULA[63][-535062077][0]が対象とする五角形 ${\rm Hol}C_5$が対象とする五角形

の4種類を自由に行き来することができ, このような群を${\rm Hol}C_5$と表記する. 厳密には

Holomorph

$G$を群とする. このとき,
\begin{eqnarray} \rho:{\rm Aut}G&\longrightarrow&{\rm Aut}G\\ \psi&\longmapsto&(g\mapsto\psi(g)) \end{eqnarray}
によって定められた半直積$G\rtimes_\rho{\rm Aut}G$を$G$のHolomorphと呼び, ${\rm Hol}G$と表記する.

のように定義され, つまりは自分自身との半直積のことである.
Holomorph, Frobenius群, 二面体群, 巡回群の4種の中ではHolomorphは多角形に対して最も寛容で対称性が高い.
Frobenius群はHolomorphが許す多角形の変形を一部禁止したもので, 例えば${\rm Hol}C_7$が許容する図形

!FORMULA[71][-535062015][0]が対象とする七角形 ${\rm Hol}C_7$が対象とする七角形

のうち, 上の段のみ(下の段でもよい)の変形を考える群である.

Fano平面の中のFrobenius群

　本題に戻って, 条件を再確認してみると,

七角形の回転を許す
鏡映反転はNG
七角形の変形が可能

と, この性質はHolomorphでも二面体群でもなく, Frobenius群に他ならない.
3つ目の七角形の変形というのは, 下図のようにグラフの接続構造を保持したままHamilton閉路を変形させる操作が存在しているということで, 例えば$\mqty(2&7&5)\mqty(3&4&6)$がこの操作に該当する.

!FORMULA[73][1607383243][0]によるHamilton閉路の循環 $\mqty(2&7&5)\mqty(3&4&6)$によるHamilton閉路の循環

以上から, 朧気だった図6の青矢印の構造が決定された. つまり, $G$は
\begin{eqnarray} \langle a,b|a^7=b^3=1,bab^{-1}=a^3\rangle \end{eqnarray}
という表示の部分群を持っており, これは位数21のFrobenius群$C_7\rtimes C_3$である.

まとめ

　${\rm Aut}S(2,3,7)$に関して, 正五胞体に埋め込むことで$\mathfrak{S}_4$, LeviグラフのHamilton閉路を観察することで$C_7\rtimes C_3$の構造を確認することができた. 群として完全に決定できたわけではないが, その骨格については理解が進んだと言って差し支えないだろう. 可能な限りFano平面から離れずに議論を進めたが, ${\rm Aut}S(2,3,9)\cong{\rm GL}_3(\mathbb{F}_2)\cong{\rm PSL}_2(\mathbb{F}_7)$と, 有限体上の線型空間でFano平面を解釈することもできる.

参考文献

[1]

Tomaž Pisanski , Brigitte Servatius, Configurations from a Graphical Viewpoint, Birkhäuser Advanced Texts Basler Lehrbücher, Birkhäuser, 2013, 170-173

投稿日：31日前

更新日：22日前