解を知らなくても無限積表示できる!?ランベルト級数でゴリ押し
今回の方法を使えば、いい感じの関数なら、解を知らなくても無限積表示を得ることができる?!
因数分解ではないことに注意。
実用性は、で、どうしよう。くらい
準備
$\mu(n)$をメビウス関数とする
$A_n=\dis\sum_{d|n}\mu\big(\textstyle\frac{n}{d}\big)a_d\qquad$ のとき、
$\dis\sum_{k=1}^{\infty}a_kx^k=\sum_{k=1}^{\infty}A_k\frac{x^k}{1-x^k}$
メビウス関数、反転公式については、他人ですが
こちらのサイト
1参考。
右辺を変形してく。
$\dis\suminf{k=1}A_k\frac{x^k}{1-x^k}$
等比級数なので
$=\dis\suminf{k=1}A_k\suminf{j=1}x^{jk}$
これを展開すると
$\begin{array}{llll} =A_1(x+x^2+x^3+x^4+x^5+x^6…)\\ \quad A_2(\quad+x^2\qquad +x^4\qquad +x^6+…)\\ \quad A_3(\qquad\quad +x^3\qquad\qquad+x^6+…)\\ \qquad\qquad\qquad\quad\qquad\vdots \end{array}$
$x^n$の係数は、$n$の約数が添字の$A$の和に等しくなる。
つまり
$\dis a_n=\sum_{d|n}A_d$
メビウス反転公式より
$\dis A_n=\sum_{d|n}\mu(\textstyle\frac{n}{d})a_d$
本題
簡単な式変形で無限積が現れる。
$f(x)=\dis\suminf{k=1}a_kx^k$
であるとする。(定数項が0の関数)
ランベルト級数にすると
$f(x)=\dis\suminf{k=1}A_k\frac{x^k}{1-x^k}$
$x$で割る
$\dis\frac{f(x)}{x}=\suminf{k=1}A_k\frac{x^{k-1}}{1-x^k}$
0からxまで積分
しれっと項別積分
左辺、発散しそうな気がするけど$f(x)$は定数項が0だったので可積分。
$\dis\int_{0}^{x}\frac{f(t)}{t}dt=-\suminf{k=1}\frac{A_k}{k}\log(1-x^k)$
係数を$\log$の中にいれる
$\dis\int_{0}^{x}\frac{f(t)}{t}dt=\suminf{k=1}\log((1-x^k)^{-\frac{A_k}{k}})$
$\log$の和は、積の$\log$なので
$\dis\int_{0}^{x}\frac{f(t)}{t}dt=\log\prodinf{k=1}(1-x^k)^{-\frac{A_k}{k}}$
きたー。
よって、関数$g(x)$の無限積表示が欲しいなら、
$\dis g(x)=\exp\Bigg(\int_{0}^{x}\frac{f(t)}{t}dt\Bigg)$
となる$f(x)$の、テイラー展開ができればいい。
それはつまり$f(x)=\dis\frac{xg’(x)}{g(x)}$。
$g(x)$が$x=0$で正則であれば$f(x)$は定数項が0となる。
また、対数微分の性質から、定数倍が消えるので、$g(0)=1$である事が必要
↑説明になってるか、?
結論
結局、まとめると
$f(x)に対し、f(0)=1で、$
$x=0あたりで正則なら$
$a_n=\dis\frac{1}{n!}\frac{d^n}{dx^n}\Bigg|_{x=0} \frac{xf’(x)}{f(x)}$
$A_n=\dis\sum_{d|n}\mu\big(\textstyle\frac{n}{d}\big)a_d$
$とすると、$
$\dis f(x)=\prodinf{k=0}(1-x^k)^{-\frac{A_k}{k}}$
ただし、因数分解ではないので、収束する範囲は限られる。
多分、$|x|<1$に解も極も無ければ範囲は$|x|<1$、あればそこまで。但しこれは予想。
例
これによる無限積を紹介。
指数関数、五角数定理のやつ。
指数関数の無限積表示って、案外珍しい?
$e^x$
$f(x)=e^x$とすると、$f(0)=1$で、これは正則関数。
$\frac{xf’(x)}{f(x)}=x$より、
$a_n=\Bigg\{\begin{array}{ll}1 \qquad (n=1) \\ 0 \qquad (otherwise) \end{array}$
よって
$A_n=\mu(n)$
という事で
$e^x=\dis\prodinf{k=1}(1-x^k)^{-\frac{\mu(k)}{k}}$
ほんまかいな って感じだが、グラフを見ると
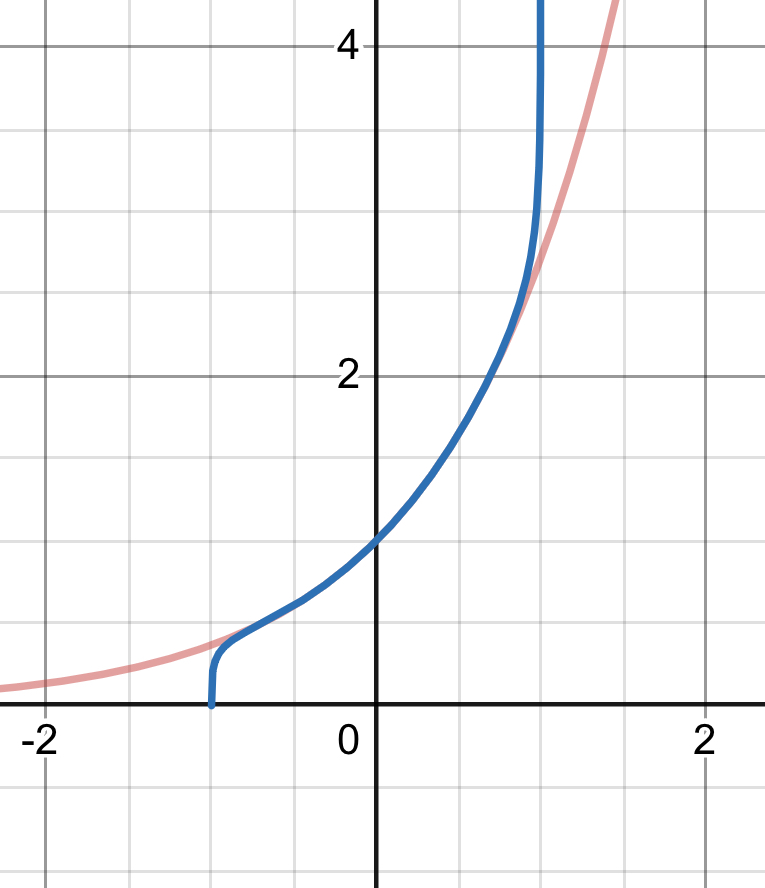
薄い赤が$e^x$
青が無限積を$k=10$で止めたもの
うおお。
収束もはやそう。
約数関数の母関数
約数関数
$\dis\sigma(n)=\sum_{d|n}d$
の母関数
$G(x)=\dis\suminf{k=1}\sigma(k)x^k$
に対し、
$f(x)=\dis\exp\Bigg(\int_{0}^{x}\frac{G(t)}{t}dt\Bigg)$
とした関数
つまり$a_n=\sigma(n)$となる。
メビウス反転公式から、
$A_n=n$
よって
$f(x)=\dis\prodinf{k=1}\frac{1}{1-x^k}$
これと、オイラーの五角数定理を使えば、約数関数の漸化式が得られる。
おわりに
自分で思いついて、書いただけなので、本題については参考文献ありません
最初の項別積分とか、収束半径(そもそも半径かも分からん)とか、詳しくしてないとこがあるので、もっと条件がある気がしなくもない。
間違い等あれば指摘ください
