高校生のための大学数学入門 トポロジー編
幾何学とは図形を調べる学問である。したがって、図形を分類することは究極の目標の一つである。トポロジーを気持ちだけでも理解することを目指す。したがって厳密性には目を瞑っていただきたい。
扱う図形を平面上の三角形に限定し、三角形の変形を考える。ここでの用語は一般的なものではなく、感覚だけ掴めればよい。(そもそもとして全く厳密ではないので)
(1)変形$f$に対し、$f\circ g,g\circ f$が何も変えないとき、変形$g$は$f$の逆変形という。
三角形$X$に対しそれを2倍にする変形$f$は、逆変形を持つ。それは1/2倍する変形$g$であり、実際$f\circ g,g\circ f$は何も変えない変形である。したがって、
(2)$k$倍する変形($k\neq 0$)は逆変形を持つ。
(3)二つの三角形$X,Y$は、三角形を$k$倍する変形$f$が存在して($k\neq 0$)、$f(X)=Y$ならば相似であるという。このとき、$f$を相似変形という。
もし二つの三角形が相似であることを示したかったら、この$k$を探せばよい。しかし、相似でないことを示すにはどうすればいいだろうか。本来、これは簡単ではない。なぜなら無数にある相似変形を調べて移り変わらないことを示さなくてはならないからである。中学数学では、相似ならば角度や辺の長さの比といった情報が不変であったことを利用して、相似でないことを示すことができた。
三角形だけでなく、より複雑な図形を扱うために連続な変形を考える。
図形を自由に伸ばしたり、縮めたりする変形を連続変形という。ただし、千切ってはいけない。逆変形を持つ連続変形を同相変形という。二つの図形$X,Y$は、同相変形$f$が存在して$f(X)=Y$を満たすとき、同相であるという。
逆変形を持つ連続変形といってもイメージが掴みづらいかもしれないが、これは図形上の相異なる二点が重ならないことを要請している。どんな図形も連続変形によって一点にできる。これは面白くないから、同相変形を中心に考える。
二つの図形$X,Y$が同相であることを示すためには、$X$を切り貼りせずに、伸ばしたり縮めることで$Y$にできることを示せばよい。
(1)多角形は全て互いに同相である。また円板とも同相である。
(2)正多面体は全て互いに同相である。また球面とも同相である。
(3)次の二つは同相である。
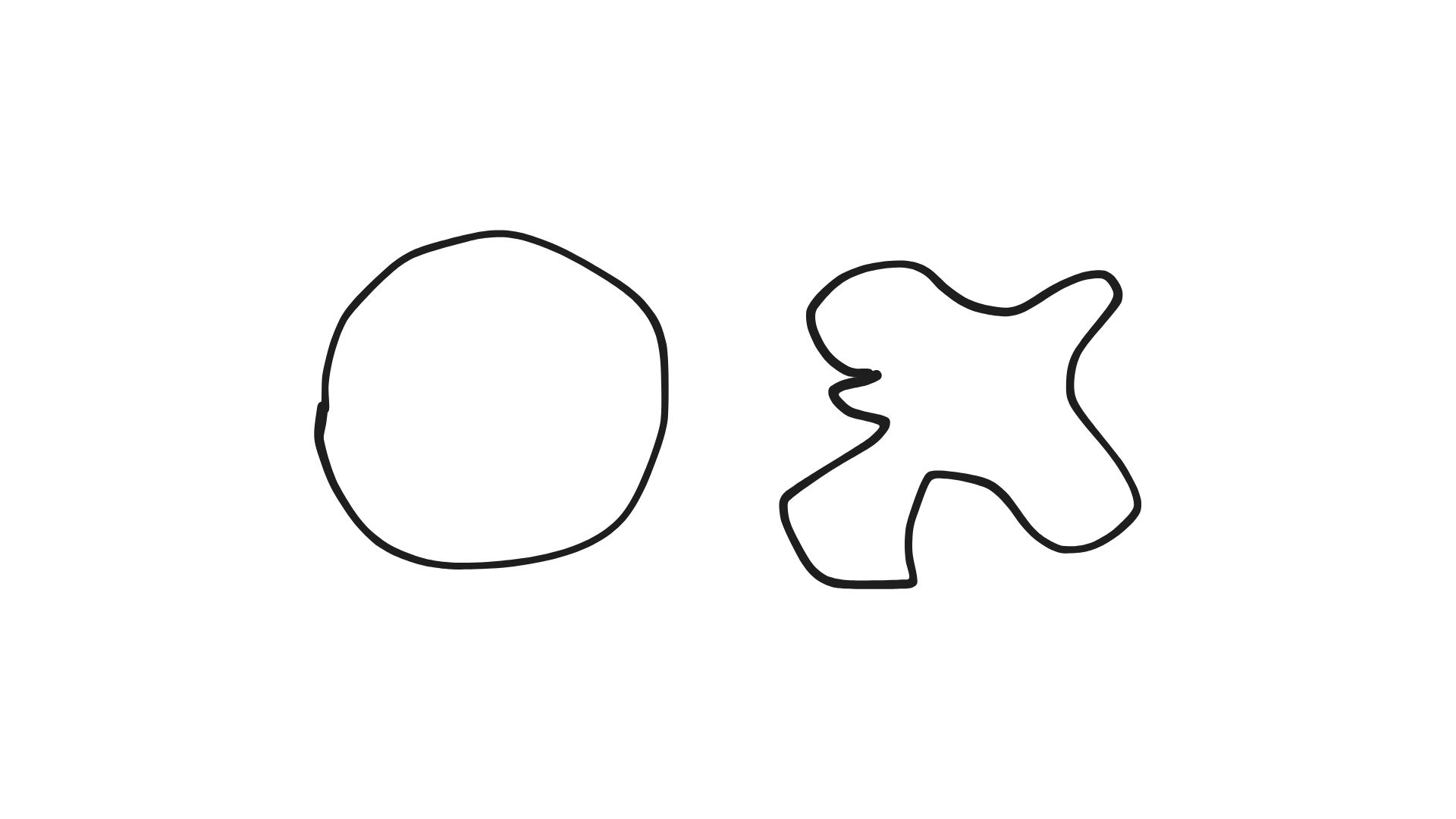
では、同相でないことを示すにはどうしたらよいか。相似と同様に、変形によって不変なものを調べることで示すことができる。変形に対し、不変な情報を不変量といい、特に同相変形の不変量を位相不変量という。
正多面体$X$に対し、$X$の頂点の数を$v(X),$辺の数を$e(X),$面の数を$f(X)$とおく。このとき、$v(X)-e(X)+f(X)=2$が成り立つ。
この定理を利用して、向きづけ可能な連結閉曲面の分類を目指す。例えば球面がそうであるが、用語の説明をしよう。
閉：どこまで進んでも行き止まり(ふち)がない。
向きづけ可能：外側と内側という区別がある。
連結：二つに分解することができない。
以下、単に図形と呼ぶ。
図形に対し、その表面を三角形で分割する。例えば球面の赤道上に4点取る。北極に1点とり、そこから赤道の4点に1本ずつ線を結ぶ。南極に1点とり、そこから同様に赤道の4点に1本ずつ線を結ぶ。点と線の情報だけ見たら、これは正八面体と同じである。この考えを利用することで正多面体でなくとも、Euler標数を定義できる。
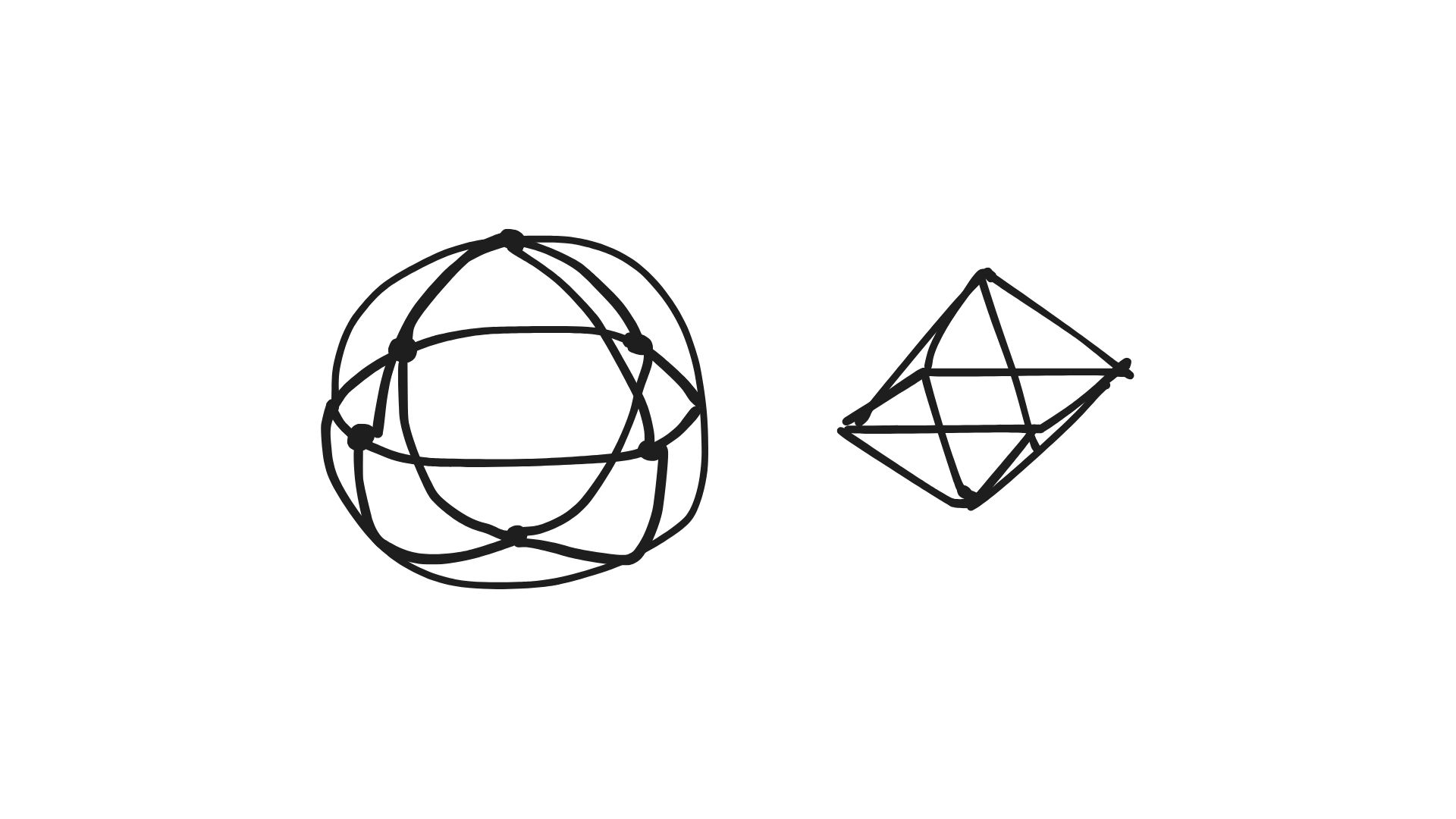図が下手でごめんね
図形$X$に対し、表面を三角形で分割する。
このとき、$χ(X)=v(X)-e(X)+f(X)$をEuler標数という。
球面$S$に対し、$χ(S)=2$
同相変形は、図形上の相異なる二点が重ならないような連続変形である。したがって、三角形で分割した図形を同相変形したとき、頂点,辺、面の個数といった情報は保存されているため、次が成り立つ。
Euler標数は位相不変量である。
すなわち、$X,Y$が同相ならば、$χ(X)= χ(Y)$が成り立つ。
球面は最も単純な図形に見える。球面と同相でない図形はどんな図形であろうか。次のような図形を考える。
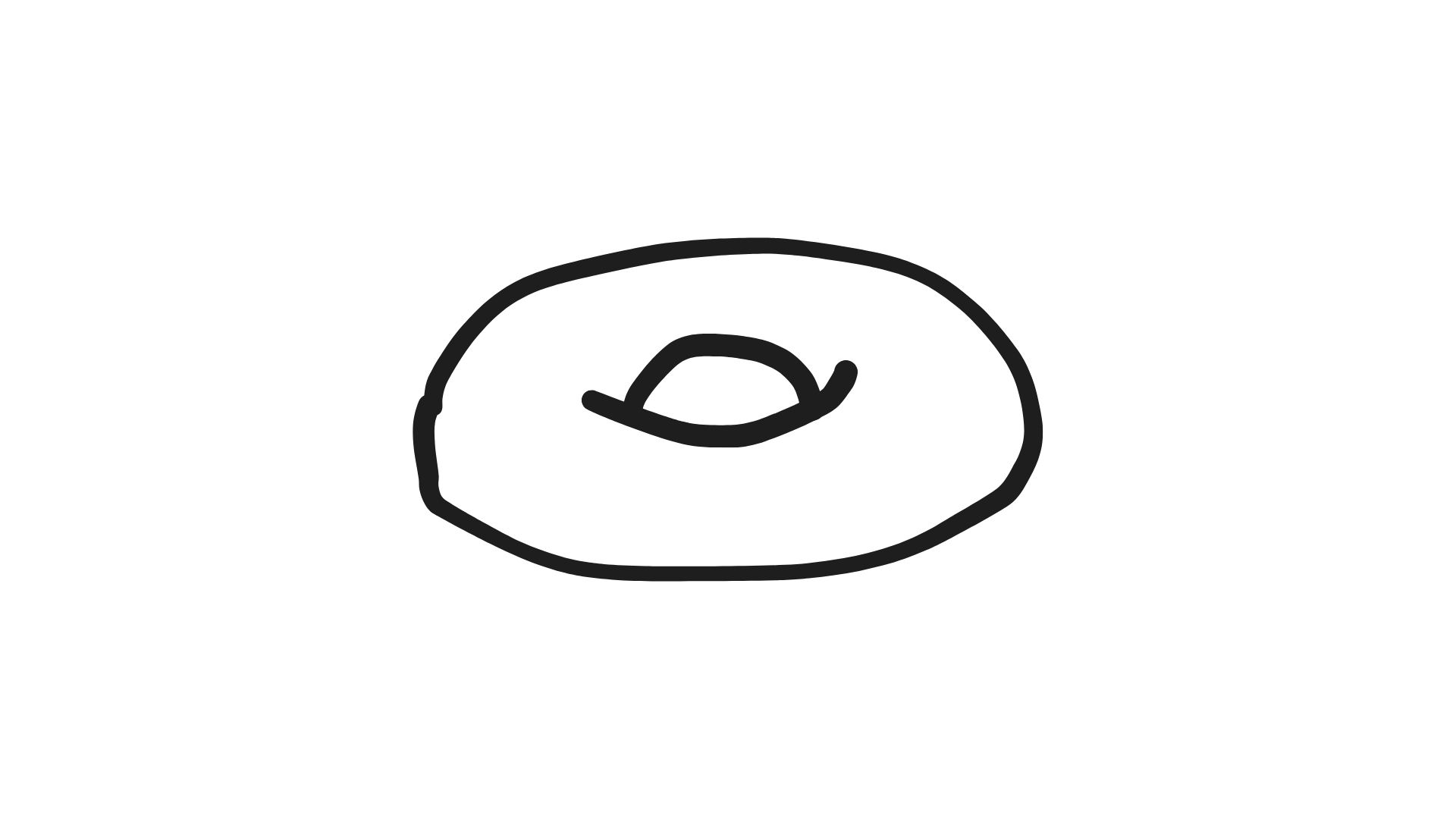トーラス
これをトーラスという。以下、$T$と書くことにする。$\chi (T)$を計算してみよう。
(1)球面$S$を三角形分割し、二つの三角形を選ぶ。
(2)その二つの三角形の穴を開ける。
(3)二つの三角形をぴったりと重ね合わせる。
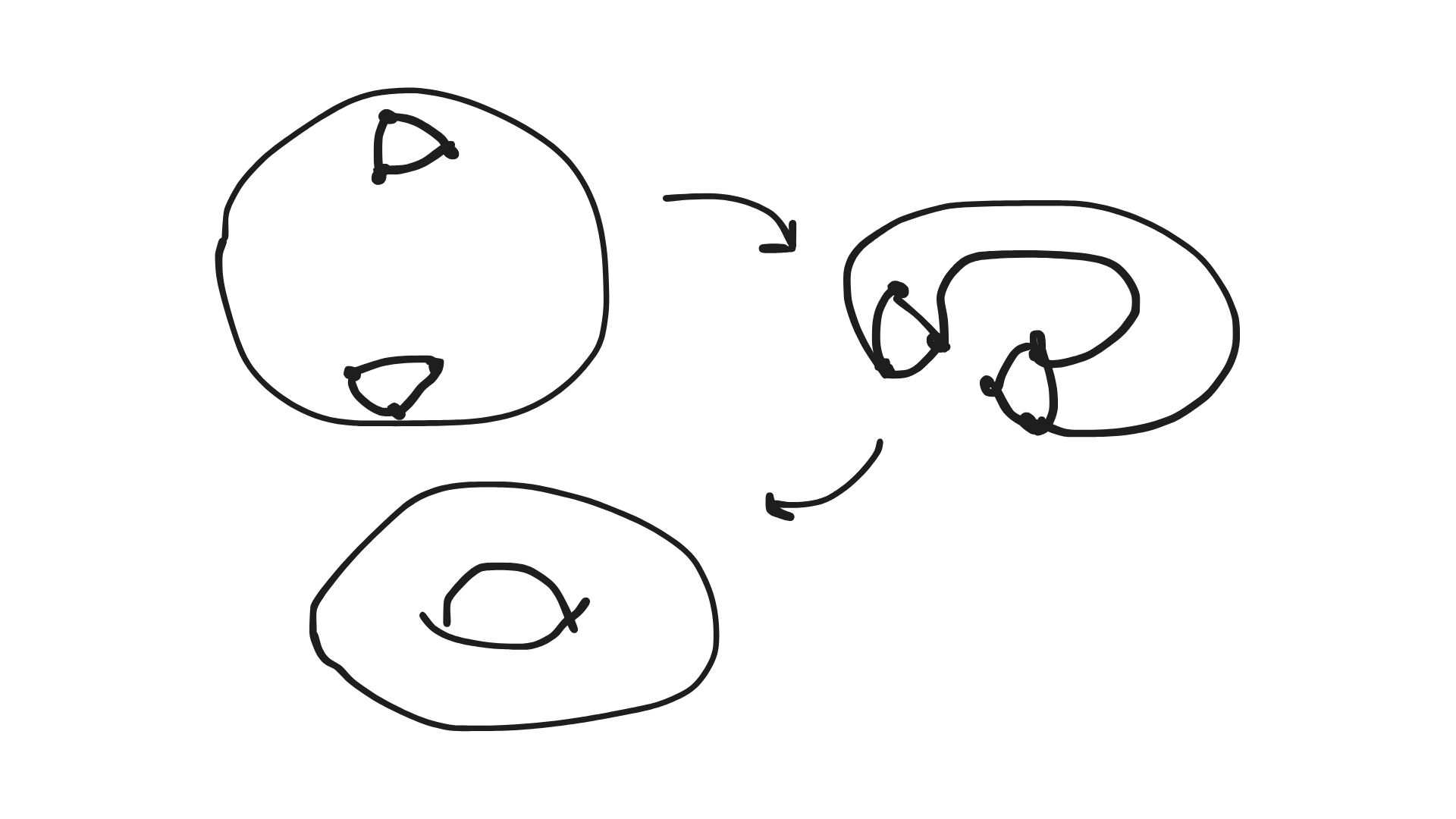球面からトーラスを作る
このとき、$\chi (T)$が$\chi (S)$からどれだけ変化しているかを見る。
まず、穴を開けているので、面の数は2個減るから、$f(T)=f(S)-2$
三角形をぴったりと重ね合わせたとき頂点の数は3個減り、辺の数も3個減るから、
$v(T)=v(S)-3,e(T)=e(S)-3$
したがって、
$\chi (T)=v(T)-e(T)+f(T)=(v(S)-3)-(e(S)-3)+(f(S)-2)=\chi(S)-2=0$
$\chi (S)\neq \chi (T)$より、$S,T$は同相ではない。
図形$X$の穴の数を種数といい、$g(X)$と書く。
先ほどの議論を繰り返すことで次がわかる。
図形$X$に対し、$\chi (X)=2-2g(X)$が成り立つ。
したがって、種数は位相不変量である。
不変量を見つけただけでは完全な分類とは呼べない。なぜなら不変量が等しくても同相でないことがあり得るからである。しかし、向きづけ可能な連結閉曲面に関しては完全に分類することができる。
向きづけ可能な連結閉曲面$X,Y$に対し、同相ならば種数が等しく、逆に種数が等しいならば同相である。
連続的な変形という、長さや角度という情報が使えない幾何学は高校までの数学とは一線を画す。しかし、変形に対して不変な情報を調べるという部分は、三角形の相似と変わらないのである。実際、それで向きづけ可能な連結閉曲面を分類することができた。幾何学の様々な分野においても、この本質は変わらない。したがって、幾何学とは不変量を調べる学問である。
