一般化マルコフ数のSL(2,Z)行列化

こんにちは、ロダンです。今回は、最近arXivで公開された行田-丸山-佐藤による論文行田-丸山-佐藤の内容の詳細について記事を書こうと思います。

論文行田-丸山-佐藤はマルコフ数（とその一般化である一般化マルコフ数）に関する新理論の論文です。ページ数でいえば80ページ近くある、数学の論文としては長い部類の論文ですが、大部分を線形代数の知識のみで理解することが可能です。さらに、この理論に登場する行列たちは整数論以外の分野においても注目されうる考察対象であると考えており、研究に取り組む学生さんや研究者の方にも広く存在を知ってほしいと考えています。この記事で行田-丸山-佐藤の内容を把握し、本論文を読む際のモチベーションや応用研究に役立てていただけたらいいなと思っています。

論文の概要

　この論文の主役は$k$一般化マルコフ数と呼ばれる整数たちです。長いので、これ以降略して$k$-GM数と呼びます。ただし、$k$は非負整数とします。この整数は、$k$一般化マルコフ方程式（こちらもこれ以降$k$-GM方程式と呼びます）と呼ばれる方程式
\begin{align} x^2+y^2+z^2+k(yz+zx+xy)=(3+3k)xyz　 \end{align}
の正整数解($k$一般化マルコフトリプル、$k$-GMトリプル)に現れる整数のことであり、例えば$k=1$の場合、$1$-GM方程式
\begin{align} x^2+y^2+z^2+yz+zx+xy=6xyz　 \end{align}
の正整数解として$(1,3,13)$がとれるので、$1,3,13$は$1$-GM数です。
特に$k=0$の場合の方程式
\begin{align} x^2+y^2+z^2=3xyz　 \end{align}
とその正整数解、そしてそれに現れる数はマルコフ方程式/マルコフトリプル/マルコフ数と呼ばれ、ディオファントス近似理論に端を発して1880年ごろにAndrei MarkovMarkov1Markov2によって導入されてから今もなお盛んに研究されている歴史ある整数です。$k$一般化の導入はそれから約150年後の2022年、行田-松下行田-松下によってマルコフ方程式の理論をより包括的に理解することを目的として導入されました。

　後述するように、$k$-GM方程式の正整数解である$k$-GMトリプルは一種の組み合わせ構造を持っており、この構造を通してマルコフ数や$k$-GM数は整数論に限らず、数学上のさまざまな分野に現れる重要な整数となっています（なっていくはずです）。ただし、実は$k$-GM数のみで構成されている「生の構造」の状態で応用を考えるのは結構難しいです。ある分野に別の分野の概念を持ち込もうとする際には、その概念自体が数学的に応用が利きやすい形で記述できている（例えばそれ自身が群の構造をもっているとか、多様体の構造を持っているとか）ことが望ましいのですが、$k$-GMトリプルからなる組み合わせ構造は、一見するとそのような良い構造があまり見えないのです。

これを解決する方法はこれまでにもいくつか知られているのですが、行田-丸山-佐藤では$k$-GM数に情報を付け足して組み合わせ構造を扱いやすい形にすることを考えています。具体的には、$k$-GM数を考える代わりに「$k$-GM数を$(1,2)$成分にもつ$SL(2,\mathbb Z)$の元」を考えて、これらが与える組み合わせ構造を観察しています。本稿ではこの増強化された$k$-GM数として扱われる$SL(2,\mathbb Z)$の元の導入と、行田-丸山-佐藤で紹介されている具体的な応用例について見ていきたいと思います。

一般化マルコフ数のツリー構造

$k$-GM数の$SL(2,\mathbb Z)$行列化を考える前に、$k$-GM数が持つ「生の」組み合わせ構造を見ておきましょう。この辺りの話は主に$k$-GM方程式を導入した行田-松下の論文行田-松下と主題である行田-丸山-佐藤の論文に基づいています。またこの部分は私の過去の記事と重複する部分がありますが、それも含めて1から説明します。まず、次のようなツリー構造を定義します。

するとこのツリーについて次が成り立ちます。

$k=0$の例をみておくことにしましょう。スペースの都合上、ツリーを90度倒した状態で表示します。

\begin{align} \begin{xy}(0,0)*+{(1,2,1)}="1",(25,16)*+{(2,5,1)}="2",(25,-16)*+{(1,5,2)}="3", (50,24)*+{(5,13,1)}="4",(50,8)*+{(2,29,5)}="5",(50,-8)*+{(5,29,2)}="6",(50,-24)*+{(1,13,5)}="7", (85,28)*+{(13,34,1)\dots}="8",(85,20)*+{(5,194,13)\dots}="9",(85,12)*+{(29,433,5)\dots}="10",(85,4)*+{(2,169,29)\dots}="11",(85,-4)*+{(29,169,2)\dots}="12",(85,-12)*+{(5,433,29)\dots}="13",(85,-20)*+{(13,194,5)\dots}="14",(85,-28)*+{(1,34,13)\dots}="15",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7"\ar@{-}"4";"8"\ar@{-}"4";"9"\ar@{-}"5";"10"\ar@{-}"5";"11"\ar@{-}"6";"12"\ar@{-}"6";"13"\ar@{-}"7";"14"\ar@{-}"7";"15" \end{xy} \end{align}

$k=1$の場合も見ておきましょう。

\begin{align} \begin{xy}(0,0)*+{(1,3,1)}="1",(25,16)*+{(3,13,1)}="2",(25,-16)*+{(1,13,3)}="3", (60,24)*+{(13,61,1)}="4",(60,8)*+{(3,217,13)}="5",(60,-8)*+{(13,217,3)}="6",(60,-24)*+{(1,61,13)}="7", (105,28)*+{(61,291,1)\dots}="8",(105,20)*+{(13,4683,61)\dots}="9",(105,12)*+{(217,16693,13)\dots}="10",(105,4)*+{(3,3673,217)\dots}="11",(105,-4)*+{(217,3673,3)\dots}="12",(105,-12)*+{(13,16693,217)\dots}="13",(105,-20)*+{(61,4683,13)\dots}="14",(105,-28)*+{(1,291,61)\dots}="15",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7"\ar@{-}"4";"8"\ar@{-}"4";"9"\ar@{-}"5";"10"\ar@{-}"5";"11"\ar@{-}"6";"12"\ar@{-}"6";"13"\ar@{-}"7";"14"\ar@{-}"7";"15" \end{xy} \end{align}

すると、(1)出てくる頂点は全て第2成分が最大であるような$k$-GMトリプルであり、(2)それぞれの解がちょうど1つでていることがわかると思います。

さて、上記のツリーでは第2成分が最も大きい$k$-GMトリプルが全て出現するようなツリーでしたが、第1成分や第3成分が最も大きい$k$-GMトリプルが出現するツリーはないの？とお考えの方もいるかもしれません。次のツリーを考えましょう。

このツリーの世代ルールは$k$-GMツリーの世代ルールを下から上に辿る変換と一致しています。だから逆$k$-GMツリーという名前がついているんですね。すると今度は次の定理が成り立ちます。

$k=0,1$の例をみておくことにしましょう。

\begin{align} \begin{xy}(0,0)*+{(1,1,1)}="1",(25,16)*+{(2,1,1)}="2",(25,-16)*+{(1,1,2)}="3", (50,24)*+{(5,2,1)}="4",(50,8)*+{(2,1,5)}="5",(50,-8)*+{(5,1,2)}="6",(50,-24)*+{(1,2,5)}="7", (85,28)*+{(13,5,1)\dots}="8",(85,20)*+{(5,1,13)\dots}="9",(85,12)*+{(29,2,5)\dots}="10",(85,4)*+{(2,5,29)\dots}="11",(85,-4)*+{(29,5,2)\dots}="12",(85,-12)*+{(5,2,29)\dots}="13",(85,-20)*+{(13,1,5)\dots}="14",(85,-28)*+{(1,5,13)\dots}="15",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7"\ar@{-}"4";"8"\ar@{-}"4";"9"\ar@{-}"5";"10"\ar@{-}"5";"11"\ar@{-}"6";"12"\ar@{-}"6";"13"\ar@{-}"7";"14"\ar@{-}"7";"15" \end{xy} \end{align}

\begin{align} \begin{xy}(0,0)*+{(1,1,1)}="1",(25,16)*+{(3,1,1)}="2",(25,-16)*+{(1,1,3)}="3", (50,24)*+{(13,3,1)}="4",(50,8)*+{(3,1,13)}="5",(50,-8)*+{(13,1,3)}="6",(50,-24)*+{(1,3,13)}="7", (85,28)*+{(61,13,1)\dots}="8",(85,20)*+{(13,1,61)\dots}="9",(85,12)*+{(217,3,13)\dots}="10",(85,4)*+{(3,13,217)\dots}="11",(85,-4)*+{(217,13,3)\dots}="12",(85,-12)*+{(13,3,217)\dots}="13",(85,-20)*+{(61,1,13)\dots}="14",(85,-28)*+{(1,13,61)\dots}="15",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7"\ar@{-}"4";"8"\ar@{-}"4";"9"\ar@{-}"5";"10"\ar@{-}"5";"11"\ar@{-}"6";"12"\ar@{-}"6";"13"\ar@{-}"7";"14"\ar@{-}"7";"15" \end{xy} \end{align}

さて、これらのツリーには次のような関係があります。

ただし、ここでの「標準的なツリー同型」とは、「ツリー同士の同型であって、左の子を与える操作と右の子を与える操作を保つようなもの」のことを指します（これ以降も同じ意味で使用します）。つまり、$\mathrm{M}\mathbb T(k)$のある頂点の第2成分を入れ替えて別の$k$-GMトリプルにすると、それは$\mathrm{M}\mathbb T^\dagger(k)$の同じ位置にある頂点の$k$-GMトリプルになるというわけです。この対応で2つの双対的なツリーは結びついています。ちなみにこの対応は2回行うと元に戻る対応なので、$\mathrm{M}\mathbb T^\dagger(k)$から$\mathrm{M}\mathbb T(k)$への標準的なツリー同型も与えることに注意してください。

一般化マルコフ数の2種類の$SL(2,\mathbb Z)$行列化

ここから本題に入っていきます。上記の$\mathrm {M}\mathbb T(k)$と$\mathrm {M}\mathbb T^\dagger(k)$の構造を増強化するために、$k$-GM数を$ (1,2)$成分に持つ$2\times 2$行列を考えます。ただし、その方法を2通り用意します。

一般化コーン行列

まずは一般化コーン行列と呼ばれる$SL(2,\mathbb Z)$行列化について。このあたりの話は行田-丸山の論文行田-丸山において導入されています。こちらは以前の私の記事でも紹介していますが、改めて導入します。

$k$-GM数は特定の3つが集まると$k$-GMトリプルを構成しますが、同様に特定の3つを集めたものを$k$一般化コーントリプルとします。

これらの定義を眺めてみると、$k$-GC行列と$k$-GCトリプルの条件(iii)の特異性が目につきますが、この条件の由来については後で説明します。

さて、これで$k$-GMトリプルの$SL(2,\mathbb Z)$行列バージョンともいうべき$k$-GCトリプルが定まりました。前述のように、$k$-GMトリプルは2つのツリー構造を持っていたわけですが、$k$-GCトリプルはどうでしょうか。まず自明解$(1,1,1)$の最初の頂点に対応する$k$-GCトリプルを考えてみましょう。

この命題の証明はそんなに難しくないです。$P$の$(1,1)$成分を$\ell$と決めてやると、$P,Q,R$が$SL(2,\mathbb Z)$に入っていること、トレースの条件、$Q=PR-S$であることから$(P,Q,R)$を決定することができます。次に$(1,1,1)$以外の場合を考えます。次のツリーを考えましょう。

最初の頂点の決め方が謎に思えるかもしれませんが、これは$(1,1,1)$に対応する$k$-GCトリプルの(2)で与えている世代ルールにおける左の子を最初の頂点とすることを意味しています。$\mathrm{M}\mathbb{T}(k)$の最初の頂点は$(1,1,1)$ではなく$(1,k+2,1)$なので、そこに合わせるための操作というわけです。右の子ではなく左の子で与えている理由は、$\ell$を$P_{1;\ell}$の$(1,1)$成分で与えているため、最初の頂点にもその情報を残しておきたいからです。さてこのように与えると、次の定理が成り立ちます。この定理が非常に重要です。

各行列の$(1,2)$成分は$\ell$に依存しないので、どんな$\ell$を取ってもこの定理は成立します。以上のことから、次の系が成り立ちます。

$k=0$でコーンツリーの具体例を見てみることにしましょう。$\ell$は何であってもいいのですが、ここでは$0$とします。
\begin{align} \begin{xy}(0,0)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&3\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{2}\\2&5\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{1}\\1&2\end{bmatrix}\right)}="1",(60,-16)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&3\end{bmatrix},\begin{bmatrix}2&\textcolor{red}{5}\\5&13\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{2}\\2&5\end{bmatrix}\right)}="2",(60,16)*+{\left(\begin{bmatrix}1&\textcolor{red}{2}\\2&5\end{bmatrix},\begin{bmatrix}3&\textcolor{red}{5}\\7&12\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{1}\\1&2\end{bmatrix}\right)}="3", (135,-8)*+{\left(\begin{bmatrix}2&\textcolor{red}{5}\\5&13\end{bmatrix},\begin{bmatrix}12&\textcolor{red}{29}\\31&75\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{2}\\2&5\end{bmatrix}\right)}="4",(135,-24)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&3\end{bmatrix},\begin{bmatrix}5&\textcolor{red}{13}\\13&34\end{bmatrix},\begin{bmatrix}2&\textcolor{red}{5}\\5&13\end{bmatrix}\right)}="5",(135,24)*+{\left(\begin{bmatrix}3&\textcolor{red}{5}\\7&12\end{bmatrix},\begin{bmatrix}8&\textcolor{red}{13}\\19&31\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{1}\\1&2\end{bmatrix}\right)}="6",(135,8)*+{\left(\begin{bmatrix}1&\textcolor{red}{2}\\2&5\end{bmatrix},\begin{bmatrix}17&\textcolor{red}{29}\\41&70\end{bmatrix},\begin{bmatrix}3&\textcolor{red}{5}\\7&12\end{bmatrix}\right)}="7",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7" \end{xy} \end{align}

$k=1$,$\ell=-1$のときは次のようになります。
\begin{align} \begin{xy}(-20,0)*+{\left(\begin{bmatrix}-1&\textcolor{red}{1}\\-7&6\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{3}\\5&16\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{1}\\3&4\end{bmatrix}\right)}="1",(40,-16)*+{\left(\begin{bmatrix}-1&\textcolor{red}{1}\\-7&6\end{bmatrix},\begin{bmatrix}3&\textcolor{red}{13}\\17&74\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{3}\\5&16\end{bmatrix}\right)}="2",(40,16)*+{\left(\begin{bmatrix}1&\textcolor{red}{3}\\5&16\end{bmatrix},\begin{bmatrix}9&\textcolor{red}{13}\\47&68\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{1}\\3&4\end{bmatrix}\right)}="3", (120,-24)*+{\left(\begin{bmatrix}-1&\textcolor{red}{1}\\-7&6\end{bmatrix},\begin{bmatrix}13&\textcolor{red}{61}\\75&352\end{bmatrix},\begin{bmatrix}3&\textcolor{red}{13}\\17&74\end{bmatrix}\right)}="4",(120,-8)*+{\left(\begin{bmatrix}3&\textcolor{red}{13}\\17&74\end{bmatrix},\begin{bmatrix}67&\textcolor{red}{217}\\381&1234\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{3}\\5&16\end{bmatrix}\right)}="5",(120,8)*+{\left(\begin{bmatrix}1&\textcolor{red}{3}\\5&16\end{bmatrix},\begin{bmatrix}149&\textcolor{red}{217}\\791&1152\end{bmatrix},\begin{bmatrix}9&\textcolor{red}{13}\\47&68\end{bmatrix}\right)}="6",(120,24)*+{\left(\begin{bmatrix}9&\textcolor{red}{13}\\47&68\end{bmatrix},\begin{bmatrix}47&\textcolor{red}{61}\\245&318\end{bmatrix},\begin{bmatrix}1&\textcolor{red}{1}\\3&4\end{bmatrix}\right)}="7",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7" \end{xy} \end{align}

各行列の$(1,2)$成分を抜き出してみると、先ほど例示したマルコフツリーに現れるマルコフトリプルに一致することが見て取れると思います。これで、$k$-GMツリー中の各成分を$k$-GC行列に増強したものとして$k$-GCツリーが与えられることがご理解いただけたかと思います。1つ注意として、$(P,Q,R)$は成分の順番を入れ替えて$(R,Q,P)$などにするとコーントリプルにはなりません。ここはマルコフとは異なるところです。$Q=PR-S$という条件があり、$PR$と$RP$は等しいとは限らないからです。

$k$-GMツリーには、$b>\max\{a,c\}$を満たすような$k$-GMトリプル$(a,b,c)$を任意にとったときに、このトリプルがツリーのどこか1箇所に現れるという性質がありましたが、$k$-GCツリーにも同じような性質があります。

次に、逆$k$-GMツリーのコーン行列バージョンである逆$k$-GCツリーも導入しておきましょう。

こちらの最初の頂点は$(P_{1;\ell},Q_{1;\ell},R_{1;\ell})$で与えています。このツリーの世代ルールは、$\mathrm{GC}\mathbb{T}(k,\ell)$の世代ルールを下から上に辿る変換に一致しています。このツリーについて、やはり次の定理が成り立ちます。

やはりこちらも次の系が成り立ちます。

次の命題も$k$-GCツリーと同様に成り立ちます。

以上から、$\mathrm{M}\mathbb{T}(k)$や$\mathrm{M}\mathbb{T}^\dagger(k)$はより情報量が多いツリーである$\mathrm{GC}\mathbb{T}(k,\ell)$や$\mathrm{GC}\mathbb{T}^\dagger(k,\ell)$の一部として実現できることがわかりました。ちなみにこの$SL(2,\mathbb Z)$行列化は、$k=0$の場合、すなわち古典的なマルコフ数の場合については1955年にHarvey Cohnが確立しておりCohn、ここで紹介したのはその$k$一般化バージョンです。$k$一般化を実現したこと自体は重要なことではありますが、新たな一つの流れを打ち立てたといえるほど大きな仕事というわけではありません。一方、次で紹介するもう1つの$SL(2,\mathbb Z)$行列化は完全に新しい概念（のはず）です。

マルコフモノドロミー行列

この小節からこの記事の終わりまでの内容は、ほぼ主題の論文行田-丸山-佐藤に基づいています。

さてここからは、一般化コーン行列とは別の$SL(2,\mathbb Z)$行列化を導入します。次の行列を考えます。

こちらも、特定の3つを集めたものを$k$-MMトリプルとします。

定義が$k$-GC行列や$k$-GCトリプルとよく似ていますが、(iii)の条件が異なっています。そしてやはりこの条件が謎。しかしどちらかというと、こちらの定義の方がシンプルであるように個人的には思います。さて、$k$-MMトリプルは定義だけではなくその性質まで$k$-GCトリプルによく似ています。まずは$(1,2)$成分が$(1,1,1)$であるような$k$-MMトリプルを決定します。

一般化コーン行列と同様、$X$の$(1,1)$成分を任意に指定するとそこから全ての値が定まります。さらに、次のツリーを考えます。

$k$-GCトリプルとのときとよく似ていますが、こちらは$k$の値によらず世代ルールが一定です（$k$-GCツリーの世代ルールには行列$S$を引くステップがあり、この$S$の成分は$k$に依存しています）。そして、次の定理が成り立ちます。

$k=0,\ell=0$の例は以下の通りです。
\begin{align} \begin{xy}(-20,0)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&0\end{bmatrix},\begin{bmatrix}-1&\textcolor{red}{2}\\-1&1\end{bmatrix},\begin{bmatrix}-1&\textcolor{red}{1}\\-2&1\end{bmatrix}\right)}="1",(60,-16)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&0\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{5}\\-1&2\end{bmatrix},\begin{bmatrix}-1&\textcolor{red}{2}\\-1&1\end{bmatrix}\right)}="2",(60,16)*+{\left(\begin{bmatrix}-1&\textcolor{red}{2}\\-1&1\end{bmatrix},\begin{bmatrix}-3&\textcolor{red}{5}\\-2&3\end{bmatrix},\begin{bmatrix}-1&\textcolor{red}{1}\\-2&1\end{bmatrix}\right)}="3", (140,-8)*+{\left(\begin{bmatrix}-2&\textcolor{red}{5}\\-1&2\end{bmatrix},\begin{bmatrix}-12&\textcolor{red}{29}\\-5&12\end{bmatrix},\begin{bmatrix}-1&\textcolor{red}{2}\\-1&1\end{bmatrix}\right)}="4",(140,-24)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&0\end{bmatrix},\begin{bmatrix}-5&\textcolor{red}{13}\\-2&5\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{5}\\-1&2\end{bmatrix}\right)}="5",(140,24)*+{\left(\begin{bmatrix}-3&\textcolor{red}{5}\\-2&3\end{bmatrix},\begin{bmatrix}-8&\textcolor{red}{13}\\-5&8\end{bmatrix},\begin{bmatrix}-1&\textcolor{red}{1}\\-2&1\end{bmatrix}\right)}="6",(140,8)*+{\left(\begin{bmatrix}-1&\textcolor{red}{2}\\-1&1\end{bmatrix},\begin{bmatrix}-17&\textcolor{red}{29}\\-10&17\end{bmatrix},\begin{bmatrix}-3&\textcolor{red}{5}\\-2&3\end{bmatrix}\right)}="7",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7" \end{xy} \end{align}

$k=1$,$\ell=0$のときは次のようになります。
\begin{align} \begin{xy}(-20,0)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&-1\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{3}\\-1&1\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{1}\\-3&1\end{bmatrix}\right)}="1",(50,-16)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&-1\end{bmatrix},\begin{bmatrix}-4&\textcolor{red}{13}\\-1&3\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{3}\\-1&1\end{bmatrix}\right)}="2",(50,16)*+{\left(\begin{bmatrix}-2&\textcolor{red}{3}\\-1&1\end{bmatrix},\begin{bmatrix}-10&\textcolor{red}{13}\\-7&9\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{1}\\-3&1\end{bmatrix}\right)}="3", (140,-24)*+{\left(\begin{bmatrix}0&\textcolor{red}{1}\\-1&-1\end{bmatrix},\begin{bmatrix}-14&\textcolor{red}{61}\\-3&13\end{bmatrix},\begin{bmatrix}-4&\textcolor{red}{13}\\-1&3\end{bmatrix}\right)}="4",(140,-8)*+{\left(\begin{bmatrix}-4&\textcolor{red}{13}\\-1&3\end{bmatrix},\begin{bmatrix}-68&\textcolor{red}{217}\\-21&67\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{3}\\-1&1\end{bmatrix}\right)}="5",(140,8)*+{\left(\begin{bmatrix}-2&\textcolor{red}{3}\\-1&1\end{bmatrix},\begin{bmatrix}-150&\textcolor{red}{217}\\-103&149\end{bmatrix},\begin{bmatrix}-10&\textcolor{red}{13}\\-7&9\end{bmatrix}\right)}="6",(140,24)*+{\left(\begin{bmatrix}-10&\textcolor{red}{13}\\-7&9\end{bmatrix},\begin{bmatrix}-48&\textcolor{red}{61}\\-37&47\end{bmatrix},\begin{bmatrix}-2&\textcolor{red}{1}\\-3&1\end{bmatrix}\right)}="7",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7" \end{xy} \end{align}
$k$-MMツリーも、各頂点の$(1,2)$成分を見ると$k$-GMトリプルを成していることがわかると思います。次の命題もGCの場合と同様に成り立ちます。

逆バージョンももちろんあります。

以上のように、$\mathrm{M}\mathbb{T}(k)$や$\mathrm{M}\mathbb{T}^\dagger(k)$は$\mathrm{MM}\mathbb{T}(k,\ell)$や$\mathrm{MM}\mathbb{T}^\dagger(k,\ell)$でも増強化できることがわかりました。このように、$k$-GC行列と$k$-MM行列は違う定義を持つのに、非常によく似た構造を持っていることが見て取れます。不思議だと思いませんか？？

一般化コーン行列とマルコフモノドロミー行列の関係性

前節で$k$-GM数の2種類の$SL(2,\mathbb Z)$行列化である一般化コーン行列とマルコフモノドロミー行列を導入して、これらが非常によく似た性質を持つことを紹介しました。ここまで類似しているからには、この2つの行列の間には何か良い関係性があるのではないかと考えるのが自然です。この節ではそれを紹介していくことにしましょう。行田-丸山-佐藤では2種類の関係性を発見しています。

2つのツリー同型$\Psi, \Phi$

突然ですが、$2\times2$行列上の次の写像$\psi\colon M(2,\mathbb Z) \to M(2,\mathbb Z)$を考えます（行列は$2\times 2$の整数成分行列であればよく、$k$-GC行列や$k$-MM行列である必要はありません）。
\begin{align} \psi\colon \begin{bmatrix} m_{11}&m_{12}\\m_{21}&m_{22} \end{bmatrix}\mapsto \begin{bmatrix} -m_{11}+m_{12}k-k&m_{12}\\m_{21}-(k+3)m_{11}+k(2k+3)(m_{12}-1) & -m_{22}+(2k+3)m_{12}-k \end{bmatrix} \end{align}
この写像は全単射写像です。実際、逆写像が次の形で与えられます。
\begin{align} \psi^{-1}\colon \begin{bmatrix} m_{11}&m_{12}\\m_{21}&m_{22} \end{bmatrix}\mapsto \begin{bmatrix} -m_{11}+m_{12}k-k&m_{12}\\m_{21}-(k+3)m_{11}-k^2(m_{12}-1) & -m_{22}+(2k+3)m_{12}-k \end{bmatrix}. \end{align}
この写像について、次の定理が成り立ちます。

それだけではありません。$\Psi\colon M(2,\mathbb Z)^3\to M(2,\mathbb Z)^3$を$\Psi(X,Y,Z)=(\psi(X),\psi(Y),\psi(Z))$で定義すると、次の定理が成り立ちます。

(2)はどういうことかというと、$\mathrm{MM}\mathbb{T}(k,\ell)$の世代ルールと$\mathrm{GC}\mathbb{T}(k,-\ell)$の世代ルールが$\Psi$で保たれることを意味しています。$\mathrm{MM}\mathbb{T}^\dagger(k,\ell)$と$\mathrm{GC}\mathbb{T}^\dagger(k,-\ell)$も然り。すなわち、図式
\begin{align} \xymatrix{ (X,Y,Z) \ar@{|->}[r]^-{\Psi} \ar@{|->}[d] & (P,Q,R) \ar@{|->}[d] \\ (X,YZY^{-1},Y) \ar@{|->}[r]_-{\Psi} & (P,PQ-S,Q)} \xymatrix{ (X,Y,Z) \ar@{|->}[r]^-{\Psi} \ar@{|->}[d] & (P,Q,R) \ar@{|->}[d] \\ (Y,Y^{-1}XY,Z) \ar@{|->}[r]_-{\Psi} & (Q,QR-S,R) } \end{align}
が可換であるということを主張しています。ただし、$\ell$は符号がひっくり返って$-\ell$になっていることに注意してください。
……なんかいきなりぽっと出た謎の写像$\Psi$が2つのツリー構造を行き来するという強烈な主張が出てきましたね。ひとまずこれで$k$-GCトリプルと$k$-MMトリプルが似たような性質を持っている理由がなんとなくわかったわけですが、そもそもこの2つのツリー構造を繋ぐ$\Psi$という写像、背後にどういう解釈があって生まれたものなのでしょうか？この疑問に対して、論文行田-丸山-佐藤の5.4節にはこう書いてあります。

The authors do not know the interpretation the another map $\Psi$, which provides a bijection between $k$-GC triples and $k$-MM triples.

わからんのかい。最初$k=0$のケースで、なんかよくわからないけどこの対応が良い関係を持ってそうだぞということがわかり、これを一般の$k$の場合に拡張した結果が$\Psi$という写像なんだそう。「なんかよくわからないけど」の部分は最後までそのままだったらしい。どういうこっちゃ。この写像の数学的に自然な解釈を見つけることができたら、それだけで論文を1本書けるんじゃないでしょうか。挑戦をお待ちしております。

なにはともあれ、なんかよくわからないけどとっても性質の良い写像$\Psi$がこの2つの$SL(2,\mathbb Z)$行列化の関係を取り持っていることがわかりました。

論文行田-丸山-佐藤は2種類の関係性を発見したと最初に書きましたが、そのもう1つもここで導入します。次で与えられる写像$\Phi\colon M(2,\mathbb Z)^3\to M(2,\mathbb Z)^3$を考えます。

\begin{align} \Phi(X,Y,Z)=(-(YZ)^{-1},-(XZ)^{-1},-(XY)^{-1}) \end{align}

この写像は$\Psi$と違い、定義から直ちにその逆写像を特定することは難しいです（というかそもそも全単射写像かどうかもよくわからない）。しかし、実は次の定理が成立します。

(2)は、$\mathrm{MM}\mathbb{T}(k,\ell)$の世代ルールと$\mathrm{GC}\mathbb{T}^\dagger(k,-\ell)$の世代ルールが$\Phi$で保たれることを意味しています。$\mathrm{MM}\mathbb{T}^\dagger(k,\ell)$と$\mathrm{GC}\mathbb{T}(k,-\ell)$も然り。すなわち、図式
\begin{align} \xymatrix{ (X,Y,Z) \ar@{|->}[r]^-{\Phi} \ar@{|->}[d] & (P,Q,R) \ar@{|->}[d] \\ (X,YZY^{-1},Y) \ar@{|->}[r]_-{\Phi} & (P,R,P^{-1}(R+S))} \xymatrix{ (X,Y,Z) \ar@{|->}[r]^-{\Phi} \ar@{|->}[d] & (P,Q,R) \ar@{|->}[d] \\ (Y,Y^{-1}XY,Z) \ar@{|->}[r]_-{\Phi} & ((P+S)R^{-1},P,R) } \end{align}
が可換であるということを主張しています。

$\Psi$との違いは、標準的なツリー同型が順方向のツリーから逆方向のツリーへのものであるという点、そして$\ell$が保存されるという点です。こちらは$\Psi$と違って、行列同士の1対1の対応があるわけではないことに注意してください。

写像$\Phi$にまつわる背景

$\Phi$は$\Psi$と比べるとなにやら複雑でよくわからない対応を持っていますが、この写像が発見されたことについてはちゃんとした背景があります。これは、$k$-GC行列の定義における、一見すると不思議な条件である(iii)と深く関わっています。これについて少し解説することにしましょう。

唐突ですが、次の方程式を考えます。
\begin{align} x^2 + y^2 + z^2 + (2k+k^2)(x+y+z) + 2k^3 + 3k^2 = xyz \end{align}
この方程式は第2$k$一般化マルコフ方程式（第2$k$-GM方程式）と呼びます。第2という名前がついている理由は、次の命題にあります。

主張(2)について、$k=0$のときは逆が成り立つことが知られていますが、一般の$k$では成り立ちません。例えば$k=4$のとき、$(9,9,22)$は第2$k$-GM方程式の正整数解ですが、これに対応する$k$-GM方程式の解は$\left(\dfrac{13}{15},\dfrac{13}{15},\dfrac{26}{15}\right)$で、整数組ではないので明らかにこれは$k$-GMトリプルではありません。第2$k$-GM方程式の正整数解で、対応する$k$-GM方程式の解が$k$-GMトリプルであるようなものを第2$k$-GM方程式における$k$-GM方程式の誘導解といいます。

さて、この命題と$k$-GC行列の定義の

を比較すると、$(1,2)$成分の値とトレースの値の間の関係性がまさに$k$-GMトリプルとそれに対応する誘導解の関係になっていることがわかります。したがって、$k$-GCトリプルの定義のうちの

は次のように書き換えることができます。

したがって、$k$-GCトリプル$(P,Q,R)$に対して次の等式が成立していることがわかります。
\begin{align} \mathrm{tr}(P)^2 + \mathrm{tr}(Q)^2 + \mathrm{tr}(R)^2 + (2k+k^2)(\mathrm{tr}(P)+\mathrm{tr}(Q)+\mathrm{tr}(R)) + 2k^3 + 3k^2 = \mathrm{tr}(P)\mathrm{tr}(Q)\mathrm{tr}(R) \end{align}

一方で、全く別の文脈において、次のような$SL(2,\mathbb C)$の元の間の恒等式が知られていました。

ここで、この恒等式と$k$-GCトリプルが満たす方程式を比較すると、次のような条件を満たす$(X,Y,Z)$があるのではないか？という疑問が浮かんできます：

この条件を$SL(2,\mathbb C)$恒等式に代入すると、$k$-GC行列のトレースに関する方程式を得ることができます（確認してみましょう）。

実は、この条件を満たす行列$(X,Y,Z)$というデザインのもとで定義されたのが$k$-MM行列と$k$-MMトリプルです。$k$-MM行列の定義のうち

が上記の(2)、$k$-MMトリプルの定義の条件

が(3)と噛み合うものであることがわかると思います。そして、$P=(-YZ)^{-1}, Q=(-XZ)^{-1},R=(-XY)^{-1}$とすることで上記の条件(1)(2)(3)を全て満たすようにできるのですが、$(X,Y,Z)$から$(P,Q,R)$への、この対応こそが写像$\Phi$です。

論文では$(P,Q,R)$をある$(X,Y,Z)$を使って$P=(-YZ)^{-1}, Q=(-XZ)^{-1},R=(-XY)^{-1}$と表す対応、すなわち$\Phi$（の制限）の逆写像のことをマルコフモノドロミー分解と呼んでいます。$\Phi^{-1}$が逆写像になることは、このマルコフモノドロミー分解が常に存在し、かつ一意的であることを意味しています。

$\Psi$と$\Phi$の関係性

この節の最後に、今まで与えた標準的なツリー同型$\Psi$と$\Phi$の関係性について言及しておくことにしましょう。異なるツリーの間の同型を与えているので、明らかにこの2つの写像は同じものではありません。しかし、これらを合成すると面白い現象が見えてきます。

写像$\mu$は$\mathrm{M}\mathbb T(k)$と$\mathrm{M}\mathbb T^\dagger(k)$の間を繋ぐ写像として前節で与えられたものです。この定理は、$\Phi\circ \Psi^{-1}$や$\Psi^{-1}\circ\Phi$が$\mu$を増強化したものであるということを意味しています。ここからさらに、次の系たちを得ます。

因数分解のような計算の困難さを持っているように見えるマルコフモノドロミー分解ですが、 $\Psi^{-1}$と$\Phi$は対応が明示的な写像なので、これらを組み合わせて計算ができるというわけです。

4点付き2次元球面における基本群の$SL(2,\mathbb C)$表現としての解釈

さて、ここまで説明してきた$k$-GCトリプルや$k$-MMトリプルを4点付き2次元球面$S^2_4$の基本群の$SL(2,\mathbb C)$表現に現れる行列だと思うと、新しい視点が見えてきます。これを説明しましょう。この節は若干専門的な話になるので、厳しそうだなと思った方は次に進んで構いません。しかし、この道の専門家にとってはおそらく非常に興味深い話だと思うので記事に残しておくことにします。

$S_4^2$の基本群（ランク3の自由群）を
\begin{align} \pi_1(S_4^2)=\langle\alpha,\beta,\gamma,\delta\mid \alpha\beta\gamma\delta=1\rangle \end{align}
で表すことにします。ここで、$\alpha,\beta,\gamma,\delta$は基点を通り4つある点のどれかを囲むようなループのホモトピー同値類だと考えることができます。この群はランク3の非可換自由群なので、$\alpha,\beta,\gamma$をその自由生成系とすることができます。したがって、$\pi_1(S_4^2)$の$SL(2,\mathbb C)$表現はこの$\alpha,\beta,\gamma$に対応する行列を決定することによって一意的に定まります。$\pi_1(S_4^2)$の$SL(2,\mathbb C)$表現全体の集合を$\mathrm{Rep}(S_4^2)$とおき、その任意の元を$\alpha$の行き先$X$, $\beta$の行き先$Y$、$ \gamma$の行き先$Z$を使って$\rho_{X,Y,Z}$と表すことにします。ここで、$(X,Y,Z)$が$k$-MMトリプルであるとすると、この$k$-MMトリプルの$\Phi$の像$(P,Q,R)$について、
\begin{align} -P=\rho_{X,Y,Z}(\gamma^{-1}\beta^{-1}), -Q=\rho_{X,Y,Z}(\gamma^{-1}\alpha^{-1}),-R=\rho_{X,Y,Z}(\beta^{-1}\alpha^{-1}), \end{align}
が成立します。以上から、$(P,Q,R)$は $(\gamma^{-1}\beta^{-1},\gamma^{-1}\alpha^{-1},\beta^{-1}\alpha^{-1})$を$SL(2,\mathbb C)$表現を通してみた形であるということができます（$-1$倍という「おまけ」がついてはいますが）。ちなみに、$k$-MMトリプルは定義から$XYZ=T$なので、$\rho_{X,Y,Z}(\delta)=T^{-1}$となっています。前節で写像$\Phi$に関する背景の話をしましたが、表現論を通してみるとこのような解釈もできるというわけです。

さて、一旦話を戻して、まだ$(X,Y,Z)$を何の条件も課さない（$k$-MMトリプルとは限らない）ただの$SL(2,\mathbb C)$の3つ組と思うことにしましょう。いま$X,Y,Z$は命題18にある方程式を満たすのですが、ここで写像$\chi\colon\mathrm{Rep}(S_4^2)\to\mathbb C^7$を次のように定めます。
\begin{align} \chi(\rho_{X,Y,Z})=(x,y,z,a,b,c,d) \end{align}
ここで、$x,y,z,a,b,c,d$は命題18で使った記号と同じです。すると、$\chi$の像は$\mathbb C^7$上の命題18の方程式を満たすような点全体からなる代数多様体（ここでは$H$とかくことにします）となるわけですが、この写像$\chi$は$\mathrm{Rep}(S_4^2)$のGIT商$\mathrm{Rep}(S_4^2)/\!/SL(2,\mathbb Z)$と$\mathbb C^7$の部分代数多様体$H$の間の同相を誘導します。これらの多様体（の同相類）は指標多様体と呼ばれます。さて、この指標多様体の同相を与える、$\chi$から誘導される同相写像を$\overline{\chi}$とします。このとき、次が成り立ちます。

この定理を見ると、$k$-GMトリプル（あるいはその誘導解）とその行列化である$k$-MMトリプルの両者は、「指標多様体の観点で考えると実は同じ点を示していて、これを代数多様体として捉えたときに出てくるものが前者、$4$点付き球面の基本群の$SL(2,\mathbb C)$表現の剰余として捉えたときに出てくるものが後者である」という解釈ができます。この観点から$k$-GCトリプルや$k$-MMトリプルを見ることで新しい応用が見つかるかもしれません。詳しい人にぜひ研究していただけると嬉しいです。

余談ですが、多様体の基本群の$GL(2,\mathbb C)$表現のことをモノドロミー表現、基本群の各元に対応する行列をモノドロミー行列と呼ぶことがあり、$k$マルコフモノドロミー行列/トリプルの名前はこれが由来となっています。

応用1：マルコフ数の2マルコフモノドロミー行列の不動点としての解釈

ここからは、前節でその定義と性質をみた$k$-GC行列や$k$-MM行列を使って、様々な分野における$k$-GM数が絡む現象を見ていきましょう。この節では、$k=2$の場合を考えます。$2$-GM数は古典的なマルコフ数、すなわち$0$-GM数と非常に深い関係があることが知られており、次の定理が成り立つことが知られています。

この節では、上記の性質から導かれる、$2$-MM行列を使ったマルコフ数の新しい解釈について見ていきたいと思います。

$2$-MM行列を1次分数変換の元とみなします。すなわち、行列$X=\begin{bmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end{bmatrix}$を、実射影直線$\mathbb{R}P^1=\mathbb R\cup\{\infty\}$に対して
\begin{align} X \cdot z:=\dfrac{x_{11}z+x_{12}}{x_{21}z+x_{22}} \quad (z\in \mathbb R) \end{align}
で作用させます。$X$が$2$-MM行列であるとき定義から$\mathrm{tr}(X)^2=4$ですが、この場合の1次分数変換は放物型と呼ばれ、この変換による $\mathbb{R}P^1$上の不動点は$x_{21}\neq 0$であれば実数上に1点だけ存在します。この不動点が有理数であることは$X$が整数成分をもつ行列であることからわかりますが、さらに次の定理が成立します。

上記の定理では不動点が無限遠点になる$x_{21}=0$の場合を除外していますが、$x_{21}=0$となるのは$X=X_{1:-1}$（記号の意味は命題9参照）のときだけであり、このとき$x_{12}=1$なので無限遠点の既約分数表示を$\dfrac{1}{0}$とみなすことで上の定理に含めることができます。さて、定理22の現象をツリー上でみることにしましょう。

定理23自体は定理22の帰結であり、取り立てて目を見張るような結果ではありません。しかし、$2$-MMツリーの世代ルールによって不動点がどのように動くのかを考えると、そこから非自明な結果が生まれます。以下、もう少し詳しく説明します。

$(X,Y,Z)\in \mathrm{MM}\mathbb T(2,\ell)$の不動点を$\dfrac{p}{p'},\dfrac{q}{q'},\dfrac{r}{r'}$としたとき、$(X,Y,Z)$の左の子は$(X,YZY^{-1},Y)$で与えられたのでした。$YZY^{-1}$の不動点は$Z$の不動点$ \dfrac{r}{r'}$を使って
\begin{align} Y\cdot\dfrac{r}{r'}=\dfrac{y_{11}\frac{r}{r'}+y_{12}}{y_{21}\frac{r}{r'}+y_{22}}=\dfrac{y_{11}r+y_{12}r'}{y_{21}r+y_{22}r'} \end{align}
と書くことができます。ここで、定理22から
\begin{align} y_{12}=q^2,\ y_{21}=-q'^2 \end{align}
です。さらに、$k$-MM行列の定義(i),(ii)から
\begin{align} &y_{11}y_{22}-y_{12}y_{21}=1\\ \Leftrightarrow\ & y_{11}(-y_{11}-k)+q^2q'^2=1\\ \Leftrightarrow\ & y_{11}^2+2y_{11}-q^2q'^2+1=0, \end{align}
同様にして$y_{22}^2+2y_{22}-q^2q'^2+1=0$を得ます。これらを解くことで$y_{11}$と$y_{12}$は$-1\pm qq'$のどちらかとなりますが、定理18から$q'$の符号と$y_{11}$と$y_{22}$の大小関係を勘案することで$y_{11}=-1-qq'$, $y_{22}=-1+qq'$で確定します。これらを$YZY^{-1}$の不動点$ \dfrac{y_{11}r+y_{12}r'}{y_{21}r+y_{22}r'}$に代入することで、$YZY^{-1}$の不動点は$\dfrac{q^2r'-qq'r-r}{-q'^2r+qq'r'-r'}$と表されます。同様にして、$(X,Y,Z)$の右の子$(Y,Y^{-1}XY,Z)$の$Y^{-1}XY$の不動点は$\dfrac{-q^2p'+qq'p-p}{q'^2p-qq'p'-p'}$となります。

さて、ここで定理23に戻ると、この2つの分数が既約であり、かつ分子が$0$より大きければこの分数の分子はマルコフ数となりますが、実際これは正しいことが示されています。これらを踏まえて、マルコフ数を計算する新しいアルゴリズムを得ることができます。

$\mathrm{P}\mathbb{T}(\ell)$の頂点の各ベクトルたちは第1成分を不動点の分子、第2成分を不動点の分母とするようなベクトルになっています。世代ルールは$ \mathrm{MM}\mathbb T(2,\ell)$の世代ルールに従って与えられる不動点の変化に基づいて設定されています。このとき、次が成立します。

具体例を見てみましょう。$\ell=0$としています。
\begin{align*} \begin{xy}(-35,0)*+{\left(\begin{bmatrix}\textcolor{red}{1}\\-1\end{bmatrix},\begin{bmatrix}\textcolor{red}{2}\\1\end{bmatrix},\begin{bmatrix}\textcolor{red}{1}\\2\end{bmatrix}\right)}="1",(10,-16)*+{\left(\begin{bmatrix}\textcolor{red}{1}\\-1\end{bmatrix},\begin{bmatrix}\textcolor{red}{5}\\1\end{bmatrix},\begin{bmatrix}\textcolor{red}{2}\\1\end{bmatrix}\right)}="2",(10,16)*+{\left(\begin{bmatrix}\textcolor{red}{2}\\1\end{bmatrix},\begin{bmatrix}\textcolor{red}{5}\\4\end{bmatrix},\begin{bmatrix}\textcolor{red}{1}\\2\end{bmatrix}\right)}="3", (60,-24)*+{\left(\begin{bmatrix}\textcolor{red}{1}\\-1\end{bmatrix},\begin{bmatrix}\textcolor{red}{13}\\2\end{bmatrix},\begin{bmatrix}\textcolor{red}{5}\\1\end{bmatrix}\right)\cdots}="4",(60,-8)*+{\left(\begin{bmatrix}\textcolor{red}{5}\\1\end{bmatrix},\begin{bmatrix}\textcolor{red}{29}\\7\end{bmatrix},\begin{bmatrix}\textcolor{red}{2}\\1\end{bmatrix}\right)\cdots}="5",(60,8)*+{\left(\begin{bmatrix}\textcolor{red}{2}\\1\end{bmatrix},\begin{bmatrix}\textcolor{red}{29}\\22\end{bmatrix},\begin{bmatrix}\textcolor{red}{5}\\4\end{bmatrix}\right)\cdots}="6",(60,24)*+{\left(\begin{bmatrix}\textcolor{red}{5}\\4\end{bmatrix},\begin{bmatrix}\textcolor{red}{13}\\11\end{bmatrix},\begin{bmatrix}\textcolor{red}{1}\\2\end{bmatrix}\right)\cdots}="7",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7" \end{xy} \end{align*}
確かに各ベクトルの第1成分がマルコフ数になっています。この形でのマルコフ数の計算方法は、私が知る限りこの論文が初出だと思います。マルコフ数の新しい性質が、もしかしたらこの計算アルゴリズムから見つかるかもしれません！もちろん、逆マルコフツリーに対応するバージョンもあります。

応用2：既約分数から$k$-GM数を構成する

次の話題は、昔私が書いた マルコフ数，擬似マルコフ数を既約分数から取り出す という記事の内容の一般化です。この記事では$k=0,1$の場合に、正の既約分数から$k$-GM数を計算するアルゴリズムを紹介していますが、これの$k$が一般のバージョンを紹介します。

ファレイツリーと$k$-GM数/$k$-MM行列/$k$-GC行列の分数ラベリング

まず、ファレイツリーと呼ばれる既約分数のツリーを導入します。

最初の方はこんな感じになります。
\begin{align*} \begin{xy}(0,0)*+{\left(\dfrac{0}{1},\dfrac{1}{1},\dfrac{1}{0}\right)}="1",(20,-21)*+{\left(\dfrac{0}{1},\dfrac{1}{2},\dfrac{1}{1}\right)}="2",(20,21)*+{\left(\dfrac{1}{1},\dfrac{2}{1},\dfrac{1}{0}\right)}="3", (55,-36)*+{\left(\dfrac{0}{1},\dfrac{1}{3},\dfrac{1}{2}\right)}="4",(55,-12)*+{\left(\dfrac{1}{2},\dfrac{2}{3},\dfrac{1}{1}\right)}="5",(55,12)*+{\left(\dfrac{1}{1},\dfrac{3}{2},\dfrac{2}{1}\right)}="6",(55,36)*+{\left(\dfrac{2}{1},\dfrac{3}{1},\dfrac{1}{0}\right)}="7",(90,-42)*+{\left(\dfrac{0}{1},\dfrac{1}{4},\dfrac{1}{3}\right)}="8",(90,-30)*+{\left(\dfrac{1}{3},\dfrac{2}{5},\dfrac{1}{2}\right)}="9",(90,-18)*+{\left(\dfrac{1}{2},\dfrac{3}{5},\dfrac{2}{3}\right)}="10",(90,-6)*+{\left(\dfrac{2}{3},\dfrac{3}{4},\dfrac{1}{1}\right)}="11",(90,6)*+{\left(\dfrac{1}{1},\dfrac{4}{3},\dfrac{3}{2}\right)}="12",(90,18)*+{\left(\dfrac{3}{2},\dfrac{5}{3},\dfrac{2}{1}\right)}="13",(90,30)*+{\left(\dfrac{2}{1},\dfrac{5}{2},\dfrac{3}{1}\right)}="14",(90,42)*+{\left(\dfrac{3}{1},\dfrac{4}{1},\dfrac{1}{0}\right)}="15",\ar@{-}"1";"2"\ar@{-}"1";"3"\ar@{-}"2";"4"\ar@{-}"2";"5"\ar@{-}"3";"6"\ar@{-}"3";"7"\ar@{-}"4";"8"\ar@{-}"4";"9"\ar@{-}"5";"10"\ar@{-}"5";"11"\ar@{-}"6";"12"\ar@{-}"6";"13"\ar@{-}"7";"14"\ar@{-}"7";"15" \end{xy} \end{align*}

このツリーについて、次の定理が成り立ちます。

定理26の証明は、例えばAignerの3.2節をみてください。このファレイツリーは、既約分数を効率よく全列挙することができるツリーであると言えます。また、世代ルールを見ると$k$-GMツリーや$k$-GCツリー、$k$-MMツリーなどと同じで、新しい値が第2成分に入り、もともと第2成分だった値が右か左にずれています。ここから、このツリーの成分と$k$-GMツリーや$k$-GCツリー、$k$-MMツリーの成分を使って、1対1の対応を作れます。これを見ていくことにしましょう。

$\mathrm{M}\mathbb{T}(k)$, $\mathrm{GC}\mathbb{T}(k,\ell)$, $\mathrm{MM}\mathbb{T}(k,\ell)$の頂点の各成分たちに、ファレイツリー$\mathrm{F}\mathbb{T}$の既約分数を使ってラベリングしていきます。例えば、$\mathrm{M}\mathbb{T}(k)$の最初の頂点は$(1,k+2,1)$ですが、ここに$\mathrm{F}\mathbb{T}$の最初の頂点$\left(\dfrac{0}{1}, \dfrac{1}{1},\dfrac{1}{0}\right)$をつかってラベル付けします。$k$-GM数$1$には既約分数$0/1$と$1/0$、$k+2$には既約分数$1/1$、というように。ここで、ラベルと$k$-GM数は1対1の関係ではないことに注意してください。続いて、各々の世代ルールを使って生まれてくる新しい$k$-GM数と新しい既約分数を順番に対応させていきます。$\mathrm{M}\mathbb{T}(k)$において最初の頂点の左の子は$(1,2k^2+6k+5,k+2)$であり、$\mathrm{F}\mathbb{T}$の最初の頂点の左の子は$\left(\dfrac{0}{1}, \dfrac{1}{2},\dfrac{1}{1}\right)$なので、新しく出てきた$2k^2+6k+5$ に既約分数$\dfrac{1}{2}$をラベリングします（既出の第1成分、第3成分の$k$-GM数と既約分数の対応はすでにラベリングしたものになっていることに注意してください）。この操作を続けていくことで、任意の$k$-GM数に既約分数がラベリングされます。既約分数$t$がラベリングされている$k$-GM数を$m_{k,t}$と書くことにします。例えば$m_{k,0/1}=1$,$m_{k,1/1}=k+2$,$m_{k,1/2}=2k^2+6k+5$です。
これと同じことを、$\mathrm{GC}\mathbb{T}(k,\ell)$と$\mathrm{MM}\mathbb{T}(k,\ell)$でも行います。$\mathrm{GC}\mathbb{T}(k,\ell)$の最初の頂点$(P,Q,R)$はそれぞれ$P=P_{1;\ell},Q=P_{1;\ell}Q_{1;\ell}-S,R=Q_{1;\ell}$だった（記号は命題４参照）ので、この3つに分数$0/1$、$1/1$、$1/0$をラベル付けし、以下世代ルールに従って$\mathrm{GC}\mathbb{T}(k,\ell)$に現れる全ての$k$-GC行列に既約分数を対応させていきます。$\mathrm{MM}\mathbb{T}(k,\ell)$では、$X_{1;\ell}$に$0/1$、$Y_{1;\ell}Z_{1;\ell}Y_{1;\ell}^{-1}$に$1/1$がラベリングされます。
既約分数$t$がラベリングされている$\mathrm{GC}\mathbb{T}(k,\ell)$の$k$-GC行列を$C_t(k,\ell)$、$\mathrm{MM}\mathbb{T}(k,\ell)$の$k$-MM行列を$M_t(k,\ell)$で表すことにします。

前置きが長くなりましたが、この節における主題は以下の問題です。

$C_t(k,\ell)$の$\ell$として$-k$を、$M_t(k,\ell)$の$\ell$として$0$をとってきているのは、そう設定するとなんかいい感じの値が出てきてくれるからです。また、定理5や定理10から、$C_t(k,-k)$の$(1,2)$成分や$M_t(k,0)$の$(1,2)$成分は$m_{k,t}$なので、ここから対応する$k$-GM数を計算することもできます。

プレ蛇グラフと正則連分数

ここから、問題1を解決するためのアルゴリズムを例を交えつつ説明します。非負整数$k$と正の既約分数$t>0$をとり、固定します。まず、傾きが$t$の線分$L_t$を$x$軸と$y$軸を固定した平面$\mathbb R^2$上にとります。ここで、この線分$L_t$の端点はどちらも整数格子点上にあって、$L_t$はそれ以外の整数格子点を通らないようなものとします。そして、整数格子点を頂点に持つ長さ1の正方形であって$L_t$が通るものを全て取り出し、その全ての正方形の左上から右下にかけて対角線を引きます。ここまでで、例えば$t=2/5$のときは下図のような図形が描けています。
$t=2/5$のプレ蛇グラフ
この図形のことを、$t$のプレ蛇グラフといいます。次に、このプレ蛇グラフの各パーツに次のルールで符号$\{+,-\}$を配置します。まず、線分$L_t$に左下から右上方向への向きを定めておきます。

1. プレ蛇グラフを分割する各直角三角形に対して：

   1. 次の条件を満たす直角三角形に$-$を配置する(図2を参照)。
      1. 線分$L_t$が左下の端点を共有している直角三角形
      2. $L_t$の進行方向の向かって左側が四角形に分割されるような直角三角形　
         $-$を配置する三角形
   2. 次の条件を満たす直角三角形に$+$を配置する(図3を参照)。
      1. 線分$L_t$が右上の端点を共有している直角三角形
      2. $L_t$の進行方向の向かって右側が四角形に分割されるような直角三角形　
         $+$を配置する三角形

2. プレ蛇グラフの内部を通る垂直線、水平線、斜線について：

   1. $L_t$上か、$L_t$の進行方向の向かって左側に中点が存在する垂直線、水平線、斜線に$-$を配置する(図4を参照)。
      $-$を配置する線分
   2. $L_t$の進行方向の向かって右側に中点が存在する垂直線、水平線、斜線に$+$を配置する(図5を参照)。 $+$を配置する線分

以上のルールに従って$t=2/5$のプレ蛇グラフに符号を配置すると次のような図を得ます。 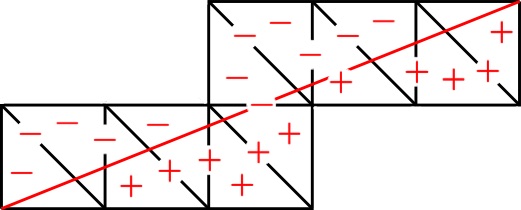符号つきプレ蛇グラフ
この符号を、線分$L$が左下から右上に向かって通る順番に並べます。ただし、直角三角形上の符号は1回カウント、線分上の符号は$k$回重複カウントしてください（$k=0$のときはカウントしません）。たとえば、$t=2/5$の例では
$k=0$のとき：　$-,-,+,-,+,+,-,-,+,-,+,+$
$k=1$のとき：　$-,-,-,-,+,+,-,+,+,+,+,-,-,-,-,-,+,-,-,+,+,+,+$
です。$k=2$と$k=3$のときも書きたかったんですが符号の数がすごいので書くのをやめました。頑張って数えてください。さらにこの符号の列をみて、同じ符号が続いている数を順番に並べ、それを使って正則連分数を構成します。
$t=2/5$の例では
$k=0$のとき：　$[2,1,1,2,2,1,1,2]$
$k=1$のとき：　$[4,2,1,4,5,1,2,4]$
$k=2$のとき：　$[6,3,1,6,8,1,3,6]$
$k=3$のとき：　$[8,4,1,8,11,1,4,8]$
になります。ただし、
\begin{align} [a_1,\dots,a_m]:=a_1+\dfrac{1}{a_2+\dfrac{1}{\ddots+\dfrac{\ddots}{a_{m-1}+\dfrac{1}{a_m}}}} \end{align}
です。この手順で得られる連分数を$F^+(k,t)$と書くことにします。連分数$ [a_1,\dots,a_m]$を既約分数に直した時の分子を$m[a_1,\dots,a_m]$と表すことにすると、この連分数を使って次のように$C_t(k,-k)$と$M_t(k,0)$が記述されます。

実際に$F^+(k,2/5)$を計算してみると、
$k=0$のとき$F^+(0,2/5)=[2,1,1,2,2,1,1,2]=194/75$
$k=1$のとき$[4,2,1,4,5,1,2,4]=4683/1075$
$k=2$のとき$[6,3,1,6,8,1,3,6]=37636/6013$
$k=3$のとき$[8,4,1,8,11,1,4,8]=176405/21501$
で分子の値が$k$-GM数になっています。本当かどうか疑わしいと思う人はファレイツリー上で$2/5$がある位置と同じ位置の$\mathrm{M}\mathbb{T}(k)$上の頂点を計算してみましょう（最初の方にあげた$\mathrm{M}\mathbb{T}(k)$の具体例では、ちょうど表示されている最後の階層で現れています）。
さて、定理27では$F^+(k,t)$の分子の値に注目していましたが、分母にも意味があります。

上記の定義は「$x$が一意的である」という非自明な主張を含んでいるので正確には命題です。また、$u_{k,t}$は$t$だけでなく$r,s$にも依存しているのではないかと思ってしまうかもしれませんが、$(r,t,s)$は$t$が決まれば一意的に決まってしまうので実は（$k$と）$t$のみに依存します。さて、実はこの特性数が$F^+(k,t)$の分母ですよというのが次なる定理です。

この特性数$u_{k,t}$は実は$F^+(k,t)=[a_1,\dots,a_m]$ としたとき$m[a_2,\dots,a_m]$で与えられる値であり、$C_t(k,-k)$の$(1,1)$成分や$M_t(k,0)$の$(2,2)$成分にも現れます。

以上、$k$-GM数には組み合わせ論的な解釈が存在するという話でした。

応用3：トーリック幾何と$k$-GM数

最後に、トーリック幾何に対する応用を見ておきましょう。この応用は応用2の更なる応用といえるかもしれません。

Hirzebruch-Jung連分数と代数多様体の特異点解消

まずは、Hirzebruch-Jung連分数（HJ連分数）を導入します。これは、先ほどの正則連分数とは異なり、項の間の演算を和ではなく差で結ぶ連分数です。すなわち、

\begin{align} b_1-\dfrac{1}{b_2-\dfrac{1}{\ddots-\dfrac{\ddots}{b_{m-1}-\dfrac{1}{b_m}}}} \end{align}
の形で表される連分数を指します。上記のHJ連分数を表す記号として、$[[b_1,\dots,b_m]]$を用いることにします。まず、この連分数がトーリック幾何の文脈でどのように用いられるかということから説明したいと思います。

$N=\mathbb Z^2$を2次元平面上の格子集合として、この格子集合を含む2次元平面$N_\mathbb R=N\otimes_\mathbb Z \mathbb R\simeq \mathbb R^2$を考えます。既約分数$d/k$に対して、$N_\mathbb R$上の$\mathbf v=(d,-k)$と$\mathbf{e}_2=(0,1)$で張られる錐
\begin{align} \sigma_{d/k}=\{a\mathbf v+b\mathbf e_2 \mid a,b\in \mathbb R_{\geq 0}\} \end{align}
を考えます。これに対して、$N$の双対格子$M=\mathrm{Hom_\mathbb Z(N,\mathbb Z)}\simeq \mathbb Z^2$ を含む2次元平面$M_\mathbb R=M\otimes_\mathbb Z \mathbb R\simeq\mathbb R^2$の錐$\sigma^\vee_{d/k}$を次で定めます。
\begin{align} \sigma^\vee_{d/k}=\{u\in M_\mathbb R \mid \forall v \in N_\mathbb R, \ u(v)\geq 0\}. \end{align}
なお、上記の集合においては$M_\mathbb R$を$\mathrm{Hom_\mathbb Z(N_\mathbb R,\mathbb Z)}$とみなしています。
$S_{d/k}=\sigma^\vee_{d/k}\cap M$を半群とみなして、$U_{d/k}$を$\mathbb C[S_{d/k}]$を座標環として持つアフィン多様体、あるいは$\mathrm{Spec}(\mathbb C[S_{d/k}])$とします。
さて、このアフィン多様体$U_{d/k}$には特異点がある場合があるのですが、この特異点が解消されたトーリック多様体は、錐$\sigma_{d/k}$を決まった位置で細かい錐に分割して、分割された各々の錐から得られるアフィン多様体を貼り合わせることによって得られることが知られています（この操作は細分と呼ばれます）。ここで、$d/k$のHJ連分数展開は、特異点を解消するために必要な細分の位置の情報を持っています。

ここで、その細分の手順を見ていきましょう。具体的に$d/k=[[b_1,b_2,\dots,b_m]]$が与えられているとします。このとき、次の操作を考えます。

1. $u_0=\mathbf e_2:=(0,1)$, $u_1=\mathbf e_1:=(1,0)$とおく。
2. 次の漸化式で、$u_2,...,u_{m+1}$を帰納的に構成する：\begin{align} u_{i+1}=b_iu_i-u_{i-1}\end{align}このとき、$u_{m+1}=\mathbf v=(d,-k)$となる。
3. 原点と端点とするような、各$u_i\ (i=2,3,\dots,m)$を通る$m-1$本の半直線で$\sigma_{d/k}$を分割する。

この操作で与えられた錐の細分（に対応するトーリック多様体）は、$U_{d/k}$の極小特異点解消を与えます。

$k$-GM数と$k$ウォールチェイン

さて、本題である$k$-GM数の話に入っていきましょう。ファレイツリーの頂点$(r,t,s)\in \mathrm{F}\mathbb{T}$を任意に取ります。これに対応する$k$-GM数$(m_{k,r},m_{k,t},m_{k,s})$を考えます。さらに、$\begin{bmatrix}\varepsilon^{m_{k,r}}&0\\0&\varepsilon^{m_{k,s}}\end{bmatrix}$ (ただし$\varepsilon$は$\varepsilon^{m_{k,t}}=1$を満たす原始冪等元)で生成される$GL(2,\mathbb C)$の部分群を$G_{k,t}$とします。2変数多項式環$\mathbb C[X,Y]$に対して$G_{k,t}$の作用を
\begin{align} \begin{bmatrix}\varepsilon^{m_{k,r}}&0\\0&\varepsilon^{m_{k,s}}\end{bmatrix}\cdot X =\varepsilon^{m_{k,r}} X,\quad \begin{bmatrix}\varepsilon^{m_{k,r}}&0\\0&\varepsilon^{m_{k,s}}\end{bmatrix}\cdot Y=\varepsilon^{m_{k,s}} Y \end{align}
でそれぞれ与え、この作用に関して不変な元全体からなる環（不変式環）を$\mathbb C[X,Y]^{G_{k,t}}$と書くことにします。このとき、実は環同型$\mathbb C[X,Y]^{G_{k,t}}\simeq\mathbb C[S_{m_{k,t}/u_{k,t}}]$が成り立ちます。したがって、$\mathbb C[X,Y]^{G_{k,t}}$を座標環として持つようなアフィン多様体の特異点解消を考えるためには、 $\mathbb C[S_{m_{k,t}/u_{k,t}}]$を座標環として持つアフィン多様体の特異点解消を考えればよく、そしてそのためには$m_{k,t}/u_{k,t}$のHJ連分数を考えれば良いことになります。$m_{k,t}/u_{k,t}$のHJ連分数展開がどのような形になるのかについて、行田-丸山-佐藤では1つの結果を与えています。これを説明しましょう。まず$k$ウォールチェインツリーを導入します。

この各頂点に属するHJ連分数を$k$ウォールチェインと呼びます。歴史的には$2$ウォールチェインの連分数表示を持つ既約分数に付随するアフィン多様体が注目されていたようです（というかそもそも$2$ウォールチェイン以外のクラスはほとんど注目されておらず、このチェインだけが「ウォールチェイン」と呼ばれていたようです）。この代数多様体は「クラス$T$」と呼ばれる良いクラスに属しており、$\mathbb Q$ゴレンシュタインスムージングだったりミルナー数が$0$だったりといろいろ良い性質を持っていて、商特異点の変形理論の文脈でいろいろ研究されているらしいです（僕は専門家ではないので詳しい話は専門家に聞いていただけるとありがたいです）。
さて、前置きが長くなりましたが、行田-丸山-佐藤では次の定理を示しています。

この定理は、${m_{k,t}}/{u_{k,t}}$の正則連分数展開が応用2で見たようにプレ蛇グラフ上の符号列を使って与えられることから示されます。特に、プレ蛇グラフ上の符号が中央の符号を挟んで左右で綺麗に対称反転の形になっていることが重要です。この性質と、正則連分数展開とHJ連分数展開の間の次の変換公式を使います。

ただし、今回の文脈で使う主張は$\ell$が偶数の時だけです。

ちなみに、定理29の逆は成り立ちません。簡単に反例を上げることができるので考えてみてください。

実はこの定理29、$k=2$の場合は2022年にMarkus Perlingが、$k=0$の場合については2023年にGiancarlo UrzúaとJuan Pablo Zúñigaが個別に示していますPerlingUrzúa-Zúñiga。したがって、この結果はその一般化となっています。ただし、2022年のPerlingの結果は$2$一般化マルコフ数とその特性数を使った形ではなく、古典的なマルコフ数の2乗数と古典的なマルコフ数の特性数を使った形で記述されているようですので、行田-丸山-佐藤の結果はPerlingとUrzúa-Zúñigaの結果を、「$k$一般化マルコフ数とその特性数」という共通のフォーマットで一般化した形であるといえそうです。

前置きしたように、$k=2$の場合についてはクラス$T$というクラスに属しているわけですが、定理29と定理21から$m_{k,t}$がマルコフ数の2乗の場合のアフィン多様体はまさにこのクラス$T$に属することがわかります。応用1でも$k=2$のときの現象を扱ったわけですが、この$k=2$のケース、そしてマルコフ数の2乗という数が、マルコフ方程式の理論周辺において何か特別な意味を持っているのかもしれません。

終わりに

文章に熱が入りすぎて結果的にかなり長い記事になってしまいました。ここまでお読みいただきありがとうございました。
この「$k$-GM数の増強化として$SL(2,\mathbb Z)$の元を考え、その構造を調べる」という研究は、去年（2023年）の6月にこの記事の筆者（行田）が糸口を掴み取って始まりました。そして大学院時代の同期である丸山さんと佐藤さんという、私とは専門分野が全く異なる2人の研究者を巻き込み、さらに様々な分野の研究者とのやりとりを通して、約1年の年月をかけて論文という1つの形にたどり着きました。この過程で様々な分野の知見が加わり、理論に厚みが出たように思います。
$k$-GM数は生まれてまだ約2年半程度（$1$-GM数は一般の$k$に先行して私が発見していますが、そこから数えてもまだ3年経っていません）で歴史が本当に浅く、現段階での$k$-GM数の業績はほぼ私とその周辺の研究者によるものに限られています。しかし、マルコフ数という元ネタが150年の間いろんな人に研究されていることを踏まえると、まだまだ底知れないポテンシャルを秘めている研究課題なのではないかと思っています。この記事で紹介した理論をもとに、様々な分野の人が各々の強みを活かして$k$-GM数の様々な性質や応用を解明していっていただけるのであれば、この記事の筆者として、そして$k$-GM数の生みの親として、大変嬉しく思います。
私がいなくなる100年後、200年後に、$k$-GM数がマルコフ数と並び立つような（というよりその理論を包含するような？）立派な概念に成長していれば嬉しいですね。ということで、この論文の公開で終わりにせず、これからも$k$-GM数の研究を頑張っていきたいと思います。