文献あり

マルコフ数，擬似マルコフ数を既約分数から取り出す

634

あいさつと概要

こんにちは，ロダンです．最近動画も出してなければmathlogも書いておらず，そろそろなにかしないとまずいような気がしているので記事を1本書きたいと思います．

今回もマルコフ数に関する話題です．マルコフ数については先日tsujimotterさんが動画をあげてくださり，以前と比べて知名度も上がっているのではないでしょうか．ということで，皆さんの関心が高まっているこのタイミングでこの整数たちについてもう少し掘り下げた現象を紹介したいと思います．まずはマルコフ数を定義することにしましょう．

マルコフ数とは，マルコフのディオファントス方程式
$\begin{array}{r} x^{2} + y^{2} + z^{2} = 3 x y z \end{array}$
の正整数解 $(x, y, z)$ に現れる正整数のことを指します．例えば， $(x, y, z) = (1, 5, 2)$ はこの方程式の正整数解なので， $1, 2, 5$ はマルコフ数です．実は，この方程式の正整数解はあるアルゴリズムを用いて全て記述することができるという話があります．例えば上記の動画や私の mathlog記事を参照してください．

さて，上記の動画やmathlog記事では，正整数解の挙動がマルコフの方程式に似ている方程式として
$\begin{array}{r} (x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z \end{array}$
という方程式が紹介されています．こちらの方程式の正整数解に現れる整数をここでは擬似マルコフ数と呼ぶことにしましょう．例えば， $(x, y, z) = (1, 13, 3)$ は上記の方程式の解なので $1, 3, 13$ は擬似マルコフ数です．どうでもいいことなのですがこの数や方程式の正式名称を誰か関連する論文を書いて決めてくれないかなと思っています．

さて，この記事のメインテーマは，このマルコフ数や擬似マルコフ数を，「既約分数から（組み合わせの数を用いて）取り出す」ことです．背景説明や細かい証明なんかをやってるとキリがなくなってしまうので現象だけの紹介に留めますが，非常に興味深い理論が背後にあります．ここで紹介する方法は，Esther Banaian氏の博士論文[1]に記述されている方法をアレンジしたものですので，詳しい証明などはこの論文を参照してください(インターネット上で公開されているので，タイトルで検索をかけたりすれば引っ掛かります)．

正の既約分数からマルコフ数を取り出す

この節では正の既約分数を使ってマルコフ数を取り出す方法について説明していきます．まず既約分数の定義について確認しておきます．ここでは以下のように定義します．

有理数の既約表示，既約分数

$q \in Q$ に対して， $n (q), d (q) \in Z$ が次の条件を全て満たすとき， $\frac{n (q)}{d (q)}$ を $q$ の既約表示という：

$q = \frac{n (q)}{d (q)}$ ,
$gcd (n (q), d (q)) = 1$ ,
$d (q) > 0$ .

さらに $\frac{a}{b}$ についてある $q \in Q$ が存在して $\frac{a}{b}$ が $q$ の既約表示であるとき， $\frac{a}{b}$ を既約分数という．

この定義によれば，通常で既約分数と呼ばれる分数の他に $\frac{2}{1}, \frac{3}{1}$ なども既約分数となります．また，負の既約分数の場合はマイナス符号は必ず分子側に付くことになります（例えば $\frac{- 1}{2}$ は既約分数であり， $\frac{1}{- 2}$ はそうではない）．ただ今回出てくる既約分数は正だけですのでマイナスについてはあまりうるさいことを考えなくても大丈夫です．強いて注意するところがあるとすれば，この定義に沿うと $\frac{- 1}{- 2}$ は既約分数ではないという点ですが，これを既約分数だと思う人は元々あまりいないんじゃないかと思っています．

さて，正の既約分数を1つ取りましょう．ここでは例として $\frac{3}{2}$ を取ります．そうしたら， $x y$ 平面上で，原点を通り，傾きがこの既約分数になるような直線を考えます．ただし，この直線のうち必要になるのは原点と格子点 $(d (q), n (q))$ を結ぶ線分の部分だけです．さらに，この線分が通る整数格子を取り出します．例として，以下に既約分数 $\frac{3}{2}$ に対応する原点と格子点 $(2, 3)$ を結ぶ線分と，それを通る格子を図示します．

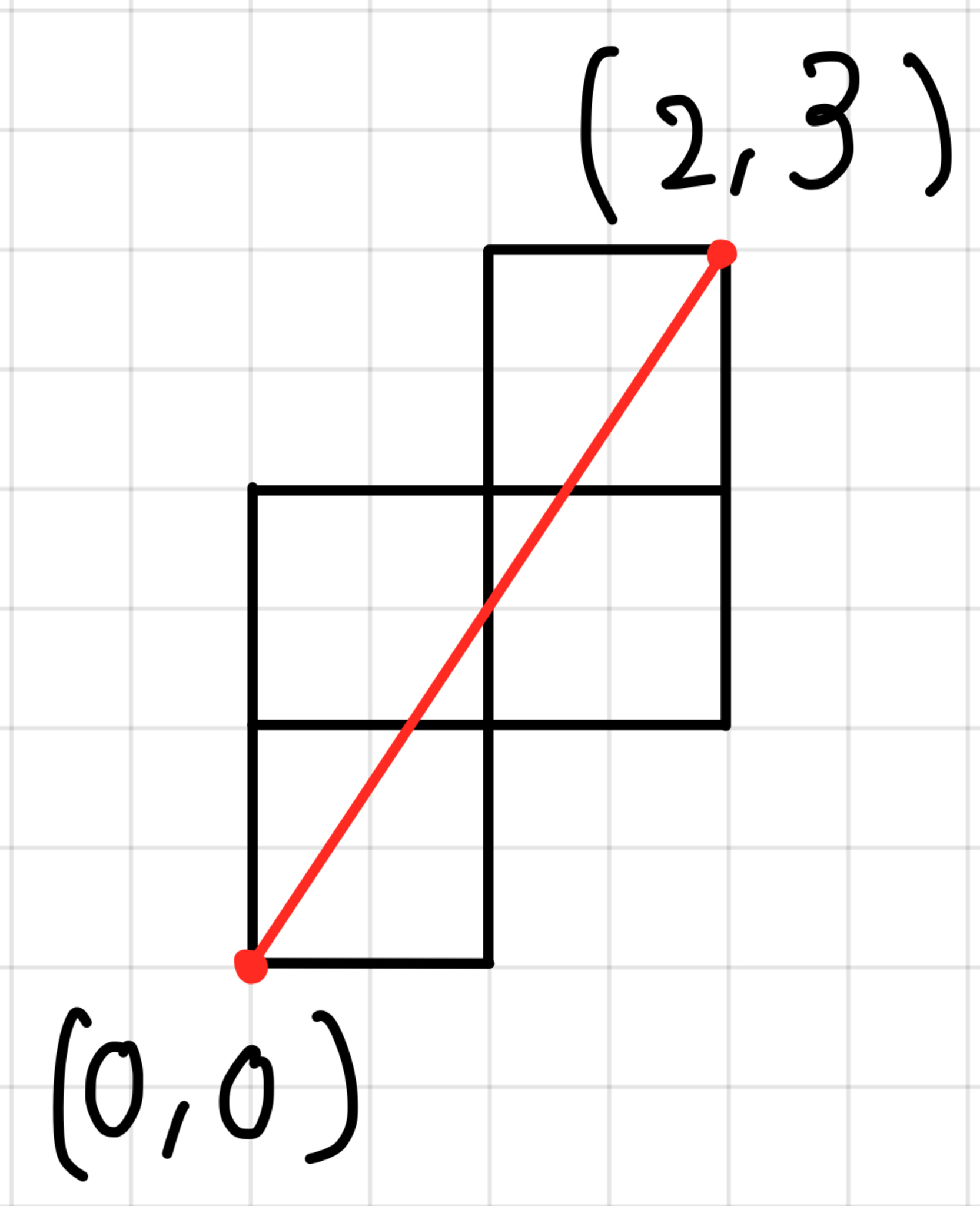既約分数3/2に対応する格子

この格子と線分を使ってマルコフ数を取り出してみましょう．まず，全ての格子に線分と交わるような対角線を引きます（図は $\frac{3}{2}$ の場合）．

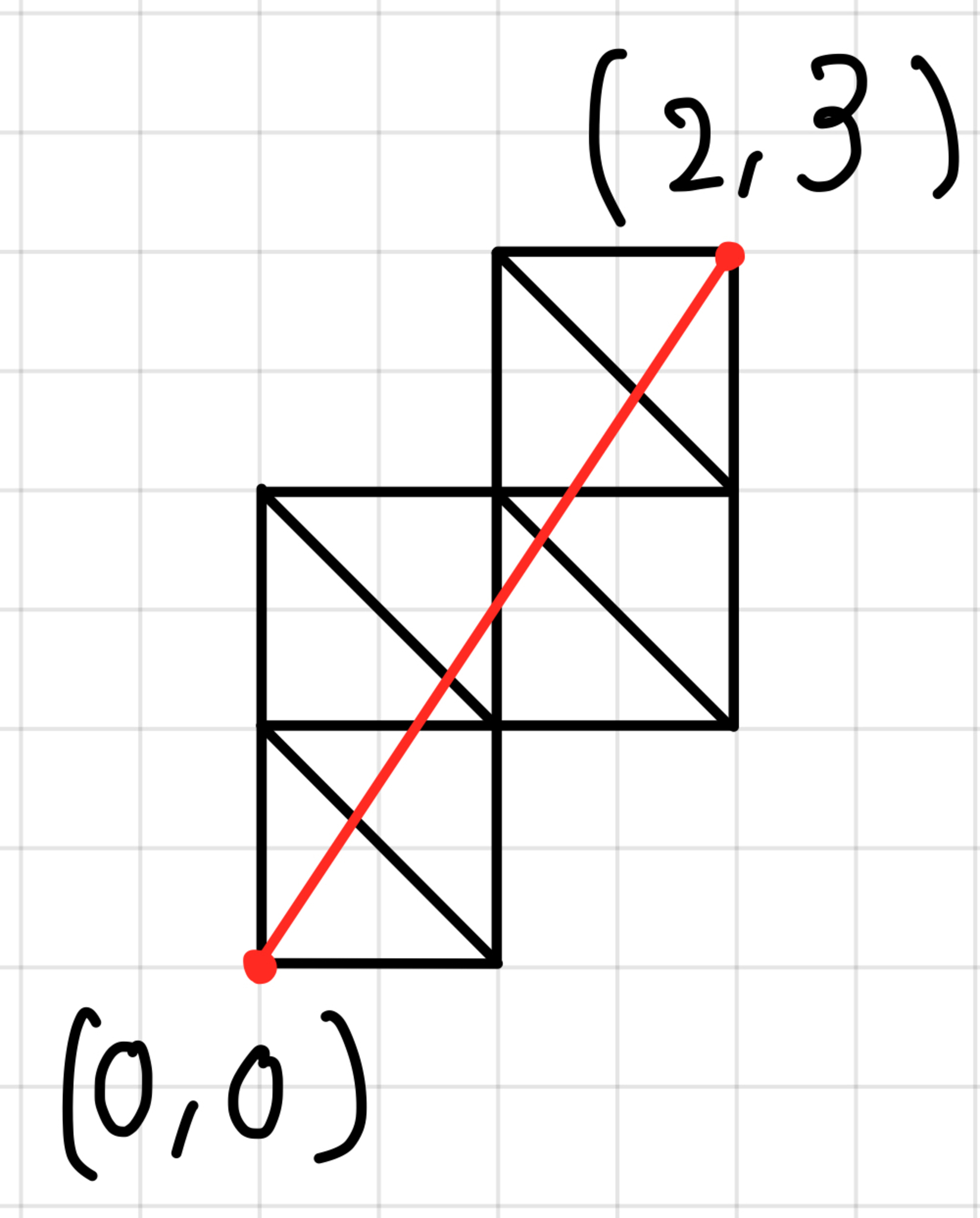既約分数3/2に対応する斜線格子

次に，線分が交わる各三角形に対して次のルールで ${+, -}$ の符号を与えます．
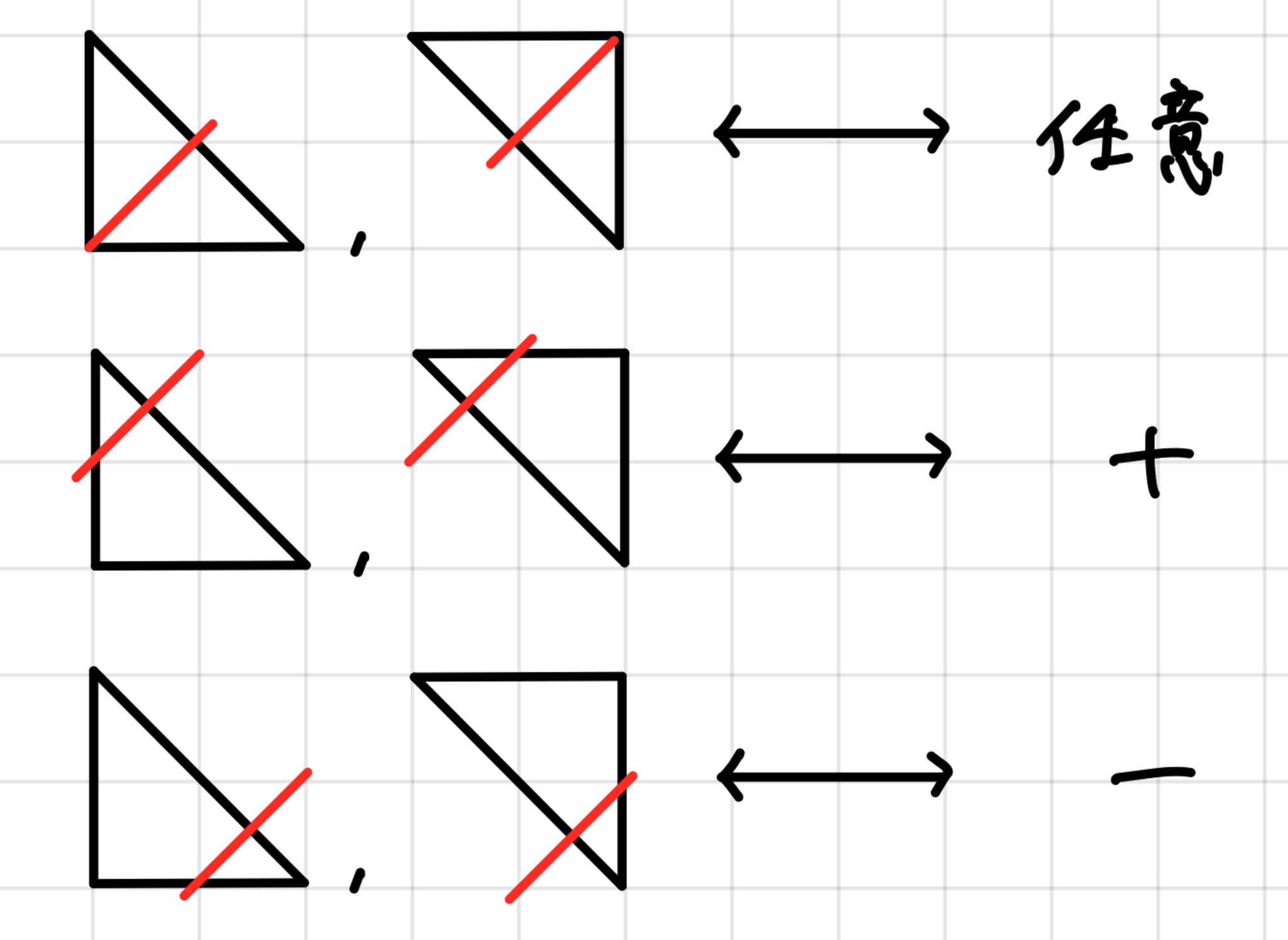三角形と符号の対応
上の図の意味を正確に述べることにしましょう．まず三角形が線分が格子点と交わっている，一番上の行の場合については三角形に与えられる符号は $+, -$ のどちらでも構いません．次に，縦辺が左にある三角形であって，縦辺と斜辺を線分が通過する場合と，縦辺が右にある三角形であって，横辺と斜辺を線分が通過する場合に符号 $+$ （2行目），縦辺が左にある三角形であって，横辺と斜辺を線分が通過する場合と，縦辺が右にある三角形であって，縦辺と斜辺を線分が通過する場合にその三角形に符号 $-$ （3行目）を与えます． $\frac{3}{2}$ の場合に各三角形に符号を与えた図が次の図です．
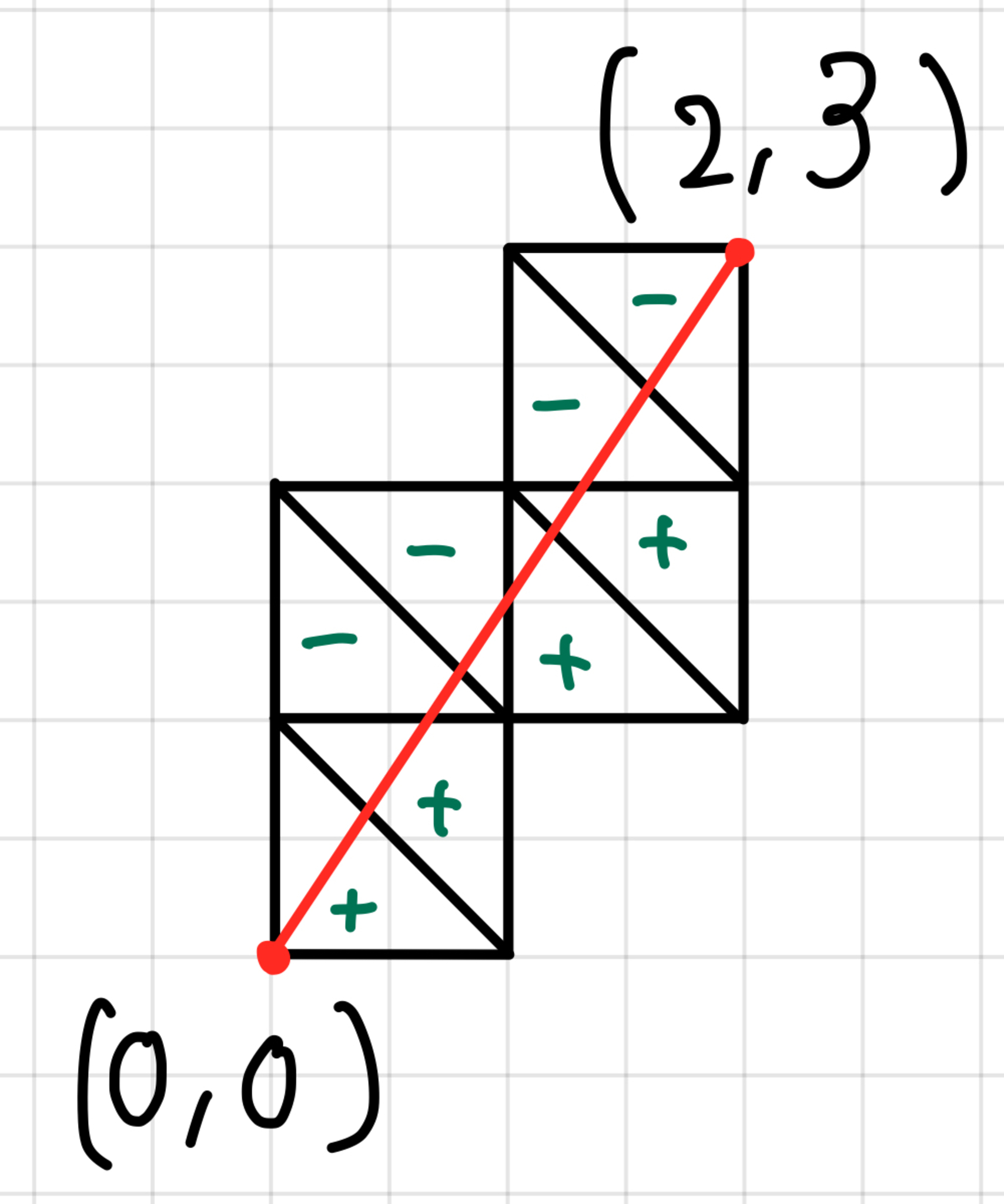符号付き斜線格子
そして，この符号を線分が通る順番に列挙します． $\frac{3}{2}$ の場合は $(+, +, -, -, +, +, -, -)$ になります．この符号の列から，同じ符号が連続する数を使って数列を作ります．上の例では $+$ が2回続いたあと $-$ が2回続き，さらに $+$ が2回， $-$ が2回続くので $(2, 2, 2, 2)$ となります．最初と最後の符号は任意なので，符号を $(-, +, -, -, +, +, -, -)$ や $(-, +, -, -, +, +, -, +)$ ， $(+, +, -, -, +, +, -, +)$ としても良いです．この場合の数列はそれぞれ $(1, 1, 2, 2, 2)$ ， $(1, 1, 2, 2, 1, 1)$ ， $(2, 2, 2, 1, 1)$ となります．

さて，この数列が $(a_{1}, a_{2}, \dots, a_{n})$ と表されるとき，次の連分数を計算します
$\begin{array}{r} [a_{1}, . . ., a_{n}] = a_{1} + \frac{1}{a_{2} + \frac{1}{a_{3} + \frac{1}{⋱ \frac{1}{a_{n - 1} + \frac{1}{a_{n}}}}}} . \end{array}$

$\frac{3}{2}$ の場合は
$\begin{array}{r} [2, 2, 2, 2] = 2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2}}} = \frac{29}{12} \end{array}$
となります．あるいは，
$\begin{array}{r} [1, 1, 2, 2, 2] = 1 + \frac{1}{1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2}}}} = \frac{29}{17}, \end{array}$
$\begin{array}{r} [1, 1, 2, 2, 1, 1] = 1 + \frac{1}{1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{1 + \frac{1}{1}}}}} = \frac{29}{17}, \end{array}$
$\begin{array}{r} [2, 2, 2, 1, 1] = 2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{1 + \frac{1}{1}}}} = \frac{29}{12} \end{array}$
としても良いです．どの場合も，（既約表示の）分子の値が同じであることがわかると思います．この分子の値を，既約分数 $\frac{p}{q}$ に対して $m_{\frac{p}{q}}$ とかくことにします．実はこの $m_{\frac{p}{q}}$ がマルコフ数となります．定理として述べておきましょう．

既約分数 $\frac{p}{q}$ から上記の方法で構成された $m_{\frac{p}{q}}$ の値は符号の取り方によらず一意的であり，これはマルコフ数となる．

例えば，上記の例で計算された $m_{\frac{3}{2}} = 29$ という値は， $(x, y, z) = (29, 5, 2)$ がマルコフのディオファントス方程式 $x^{2} + y^{2} + z^{2} = 3 x y z$ の正整数解になっているのでマルコフ数です．他の例も計算してみましょう．既約分数として $\frac{5}{3}$ をとると，三角形に付随する符号は次のようになります．

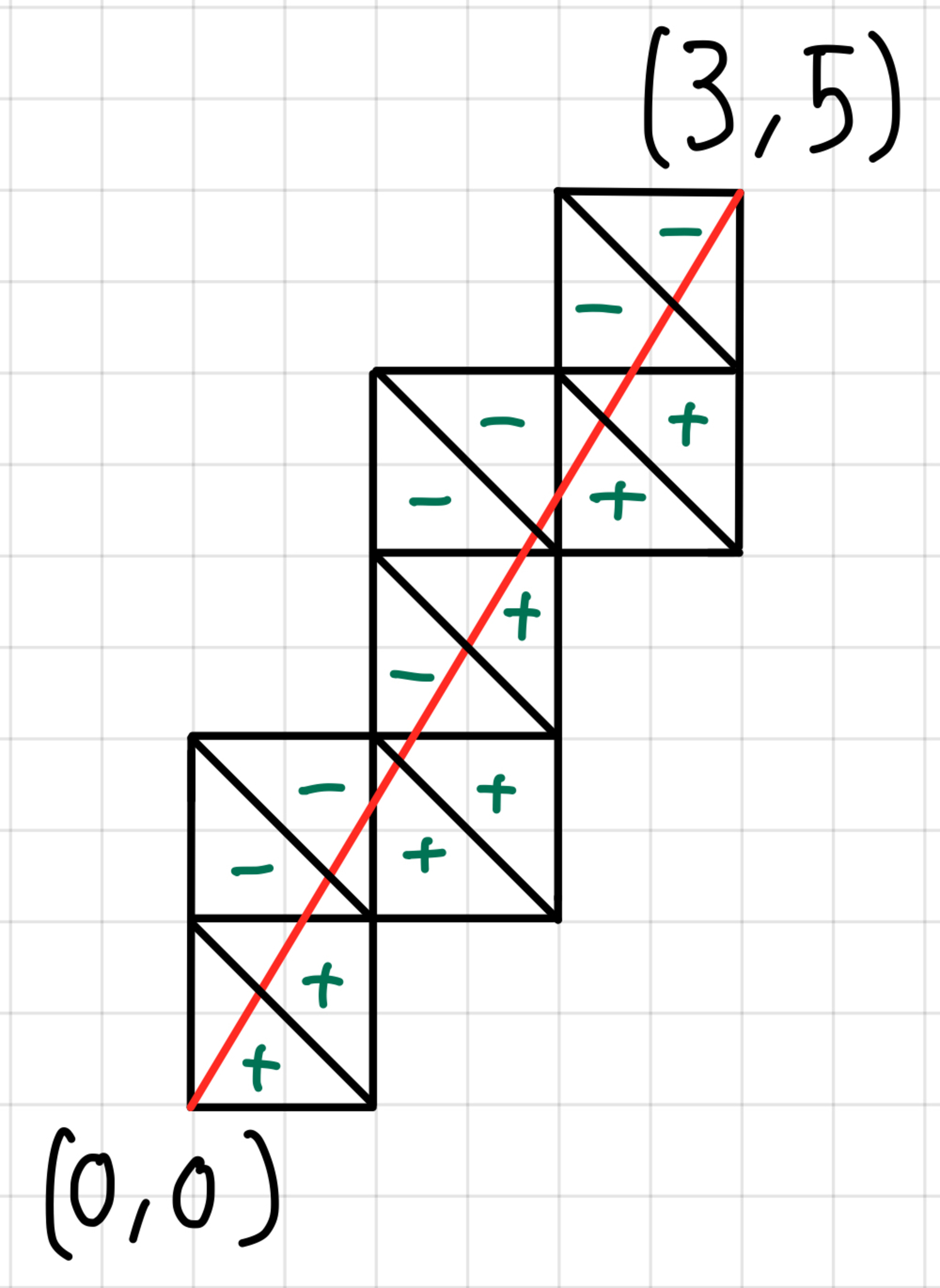既約分数5/3の例

このとき，符号の列は $+, +, -, -, +, +, -, +, -, -, +, +, -, -$ なので，対応する数列は $(2, 2, 2, 1, 1, 2, 2, 2)$ です．従って， $m_{\frac{5}{3}}$ は連分数 $[2, 2, 2, 1, 1, 2, 2, 2]$ の既約分数表示の分子となります．実際に $[2, 2, 2, 1, 1, 2, 2, 2]$ を計算してみると，これは $\frac{433}{179}$ となり， $m_{\frac{5}{3}} ＝ 433$ であることがわかります（皆さんも実際に計算してみましょう．ちなみに僕はめんどくさかったのでウルフラムアルファにぶち込みました）．ここで， $(x, y, z) = (29, 5, 433)$ は $x^{2} + y^{2} + z^{2} = 3 x y z$ の正整数解になっているので， $433$ はマルコフ数です．

ところで，マルコフ数は $x^{2} + y^{2} + z^{2} = 3 x y z$ の正整数解に現れる数ですから，解をなす3つのマルコフ数の組には特別な意味があるわけです．では，マルコフ数を構成するための既約分数の方には何か特別な意味があるのでしょうか？それを説明するための準備として，まずFareyトリプルツリーを定義します．

Fareyトリプルツリー

$(\frac{0}{1}, \frac{1}{0}, \frac{1}{1})$ から始めて， $(\frac{a}{b}, \frac{c}{d}, \frac{e}{f})$ に繋がる2つの三つ組を以下のルールで定める：真ん中の大きさの分数が (i) $\frac{a}{b}$ , (ii) $\frac{c}{d}$ , (iii) $\frac{e}{f}$ であるとき，それぞれ
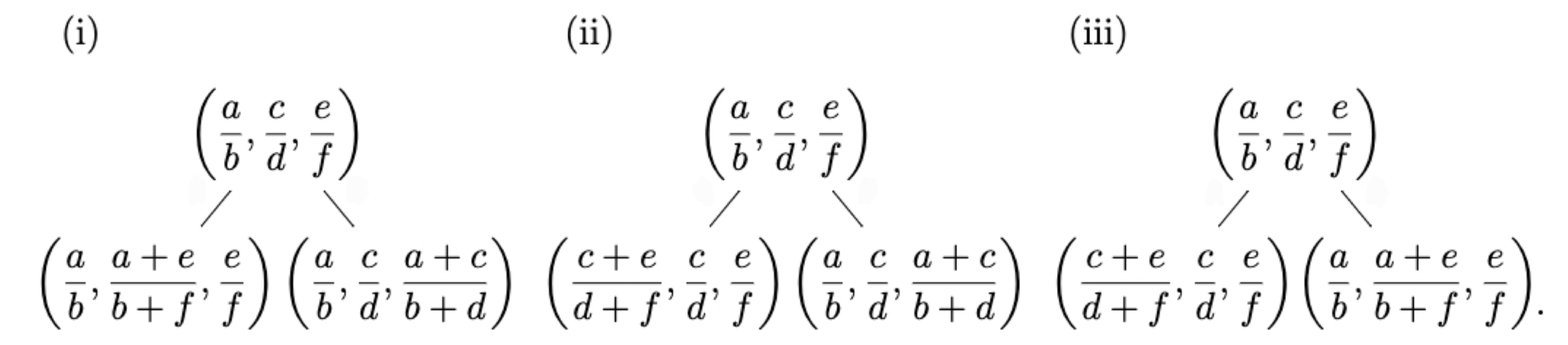Farey規則
でつながっているとする．このような樹形図を，Fareyトリプルツリーという（ただし， $\frac{0}{1}$ は $0$ として扱い，また $\frac{1}{0}$ はどのような数よりも大きい数として扱うことにする）．

このツリーの最初の方はこんな感じになってます．
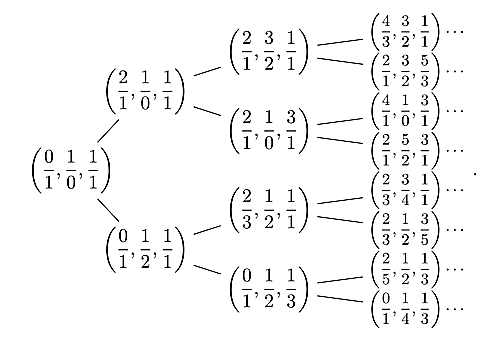Fareyトリプルツリー
ここに現れる分数は全て既約分数であることが知られています．このツリーにも興味深い性質が色々ありますが，ここではその話は割愛します（例えばこのシリーズ辺りに色々書いてあります）．さてこのとき，次の定理が成り立ちます．

Fareyトリプルツリーの頂点 $(\frac{a}{b}, \frac{c}{d}, \frac{e}{f})$ に対して， $(m_{\frac{a}{b}}, m_{\frac{c}{d}}, m_{\frac{e}{f}})$ はマルコフのディオファントス方程式の解となる（ただし $m_{\frac{0}{1}} = m_{\frac{1}{0}} = 1$ と約束する）．

特に，Fareyトリプルツリーの頂点の既約分数を全て $m_{\frac{p}{q}}$ で置き換えたツリーは次のようになり，このツリーの中央から上の部分，または中央から下の部分だけを考えると，これはマルコフの木の2列目以降に一致していることがわかります（マルコフの木の定義については例えばここを参照してください）．
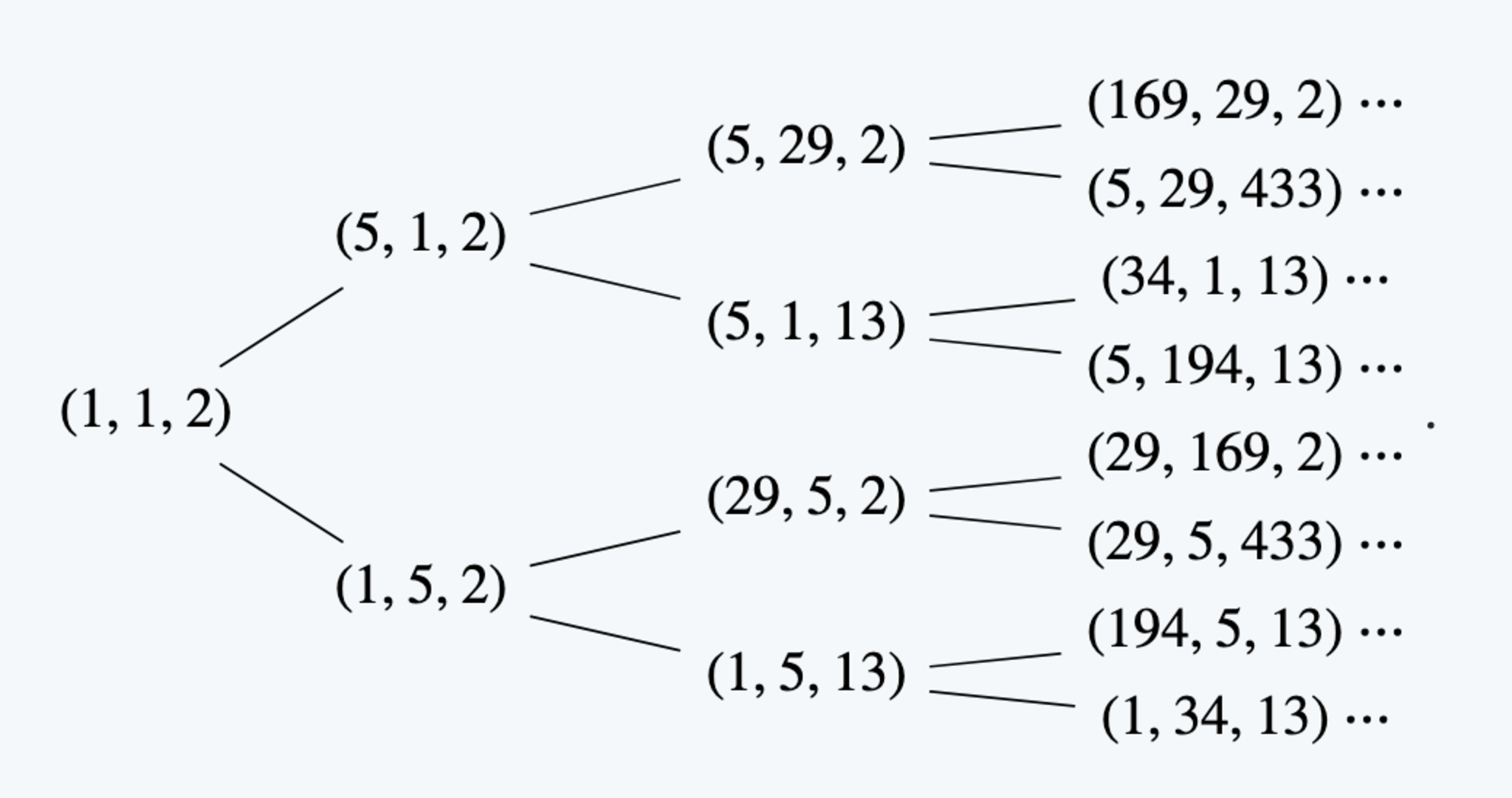拡張されたマルコフの木
ところで，正の既約分数からマルコフ数を構成する方法は上記の通りなわけですが，逆にマルコフ数が与えられた時に対応する正の既約分数はどうなっているのでしょうか？まずわかることは，1つのマルコフ数 $(\neq 1)$ に対してそれを与える正の既約分数は少なくとも2つはあるということです．例えばこれまで散々追っかけてきたマルコフ数 $29$ の例ですが，対応する既約分数は $\frac{3}{2}$ の他に $\frac{2}{3}$ があります．これは作られる格子の形状が $\frac{3}{2}$ の場合の鏡像と合同であることからすぐにわかります．そして，この格子の形状が同じになる2つの既約分数はそれぞれ「 $0$ 以上 $1$ 以下」「 $1$ 以上」の領域にあることがわかります．したがって，考える既約分数をこの2つの領域のうちのどれか1つに制限した場合，同じ形状の格子を与える正の既約分数は1つしかないことになりますが，ここで1つ疑問が浮かびます．この制限のもとで，1つのマルコフ数に対して対応する既約分数は1つなのでしょうか？言い換えると，1つのマルコフ数に対してそれを与える格子は1つなのでしょうか？実は，この問題は未解決です．

マルコフ数 $c$ に対して， $c = m_{\frac{p}{q}}$ を満たす1以上の既約分数 $\frac{p}{q}$ は一意的である．

そして，この予想はマルコフの単一性予想（この予想についてはここを参照）に同値となっています．

正の既約分数から擬似マルコフ数を取り出す

さて，次は正の既約分数から擬似マルコフ数を取り出してみましょう．手順は既約分数を傾きとする線分から格子を構成して，格子に対角線を引いて三角形の集まりとするところまではマルコフ数の場合と全く同様です（既約分数 $\frac{3}{2}$ の例でいうと図2の状態まで）．違うのは，符号の与え方です．マルコフ数の場合は三角形に対して1つ符号を与えましたが，擬似マルコフ数の場合は三角形に加えて線分と交わる三角形の各辺にも符号を与えます．ルールは次の通りです．
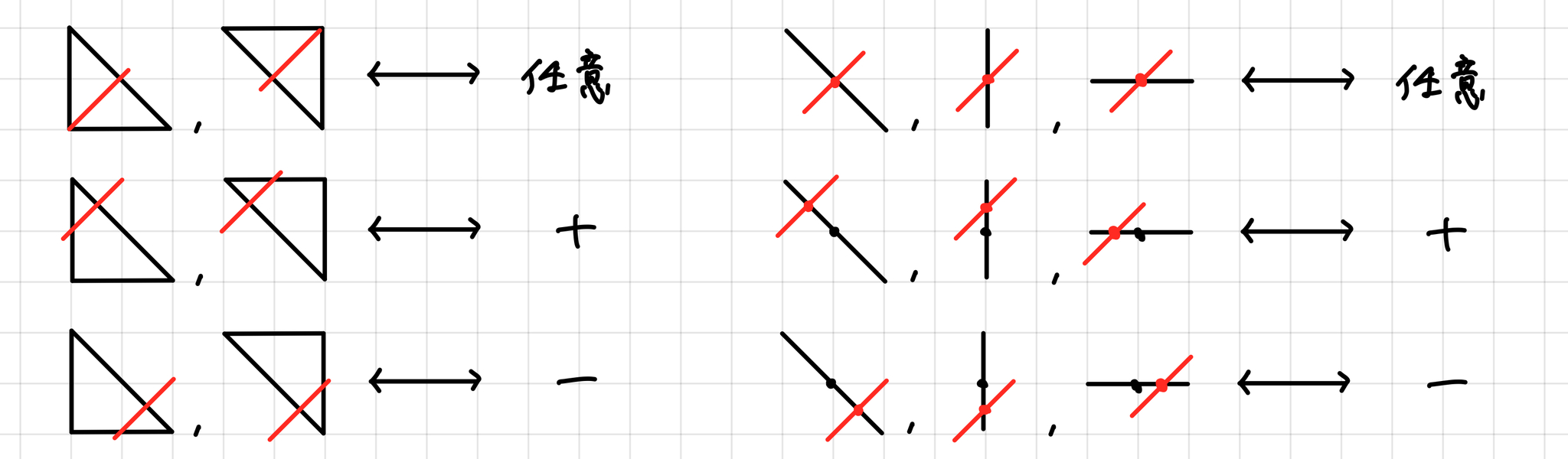三角形と線分に交わる辺と符号の対応

左半分の三角形に与える符号についてはマルコフの場合と同じです．右半分の，線分と交わる辺に与える符号のルールについて説明します．まず，三角形の辺のちょうど中央を線分が通過する場合，与える符号は $+, -$ のどちらでも構いません（1行目）．次に，三角形の斜辺と線分が中央より上，縦辺と線分が中央より上，横辺と線分が中央より左で交わる場合，それぞれの辺に $+$ の符号を与えます(2行目)．それぞれについて，中央を挟んで逆側で交わる場合はそれぞれの辺に $-$ の符号を与えます(3行目)．既約分数が $\frac{3}{2}$ の場合の例を見てみましょう．
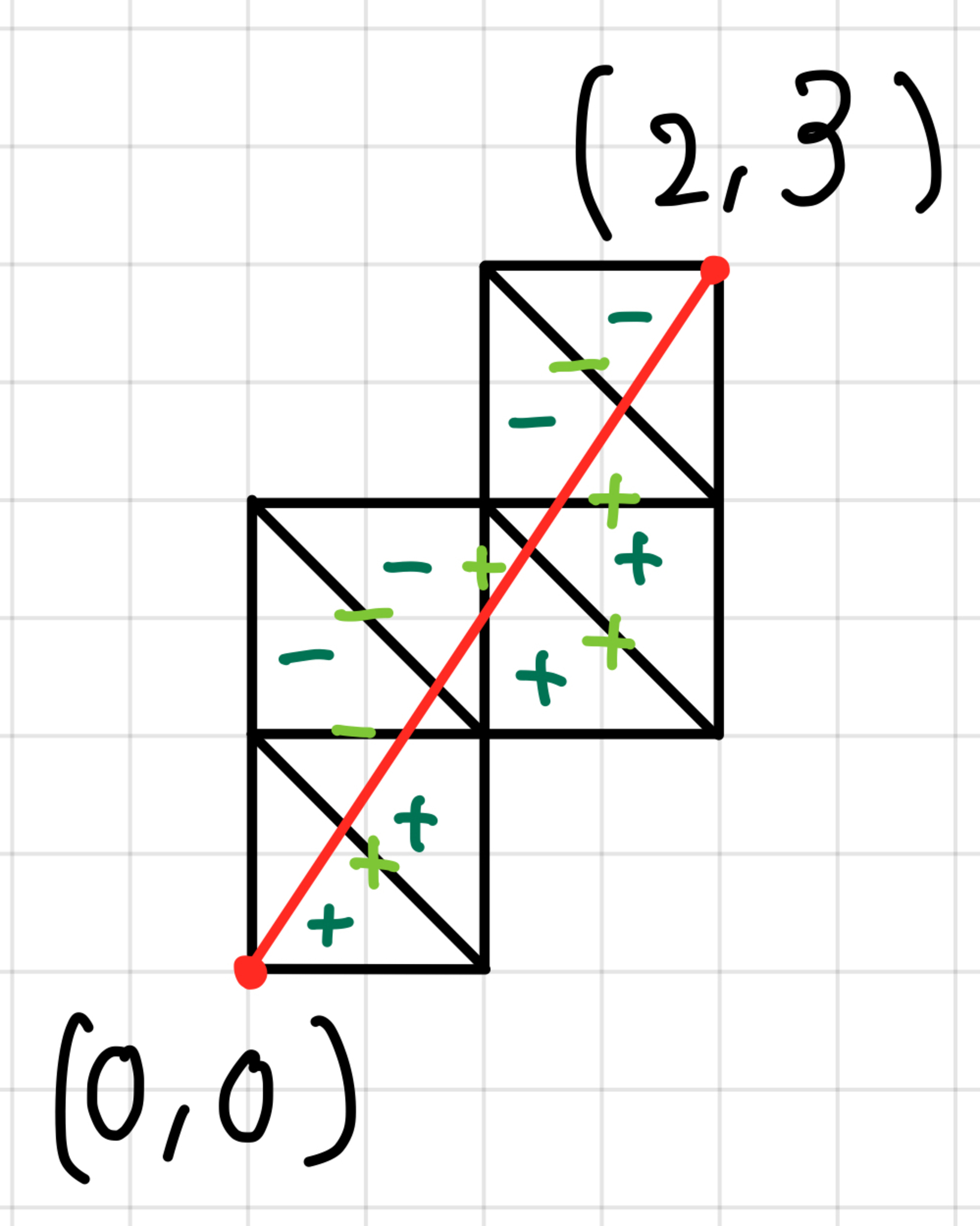符号付き斜線格子
マルコフの場合にはなかった符号を黄緑色で表しています．あとの手順はマルコフの場合と一緒で，この符号を線分が通る順番に列挙し，この符号の列から同じ符号が連続する数を使って数列を作り，連分数を計算します．上で挙げた $\frac{3}{2}$ の場合は符号が $+, +, +, -, -, -, -, +, +, +, +, +, -, -, -$ となるので，連分数 $[3, 4, 5, 3]$ を計算します．ちなみにこのケースでは最初と最後とちょうど真ん中の符号は任意なので，計算する連分数は $[1, 2, 4, 5, 3]$ とか $[1, 2, 5, 4, 3]$ , $[1, 2, 5, 4, 2, 1]$ とかでも良いです．実際に $[3, 4, 5, 3]$ を計算してみると $\frac{217}{67}$ となります．やはりマルコフの場合と同様にこの分数の分子を $M_{\frac{p}{q}}$ とすると，この $M_{\frac{p}{q}}$ は擬似マルコフ数です．定理として述べておきます．

既約分数 $\frac{p}{q}$ から上記の方法で構成された $M_{\frac{p}{q}}$ の値は符号の取り方によらず一意的であり，これは擬似マルコフ数となる．

例えば，上記の例で計算された $M_{\frac{3}{2}} = 217$ という値は， $(x, y, z) = (217, 13, 3)$ が方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の正整数解になっているので擬似マルコフ数です．マルコフの例に倣って，既約分数として $\frac{5}{3}$ をとる場合も見てみましょう．まず符号は次のようになります．

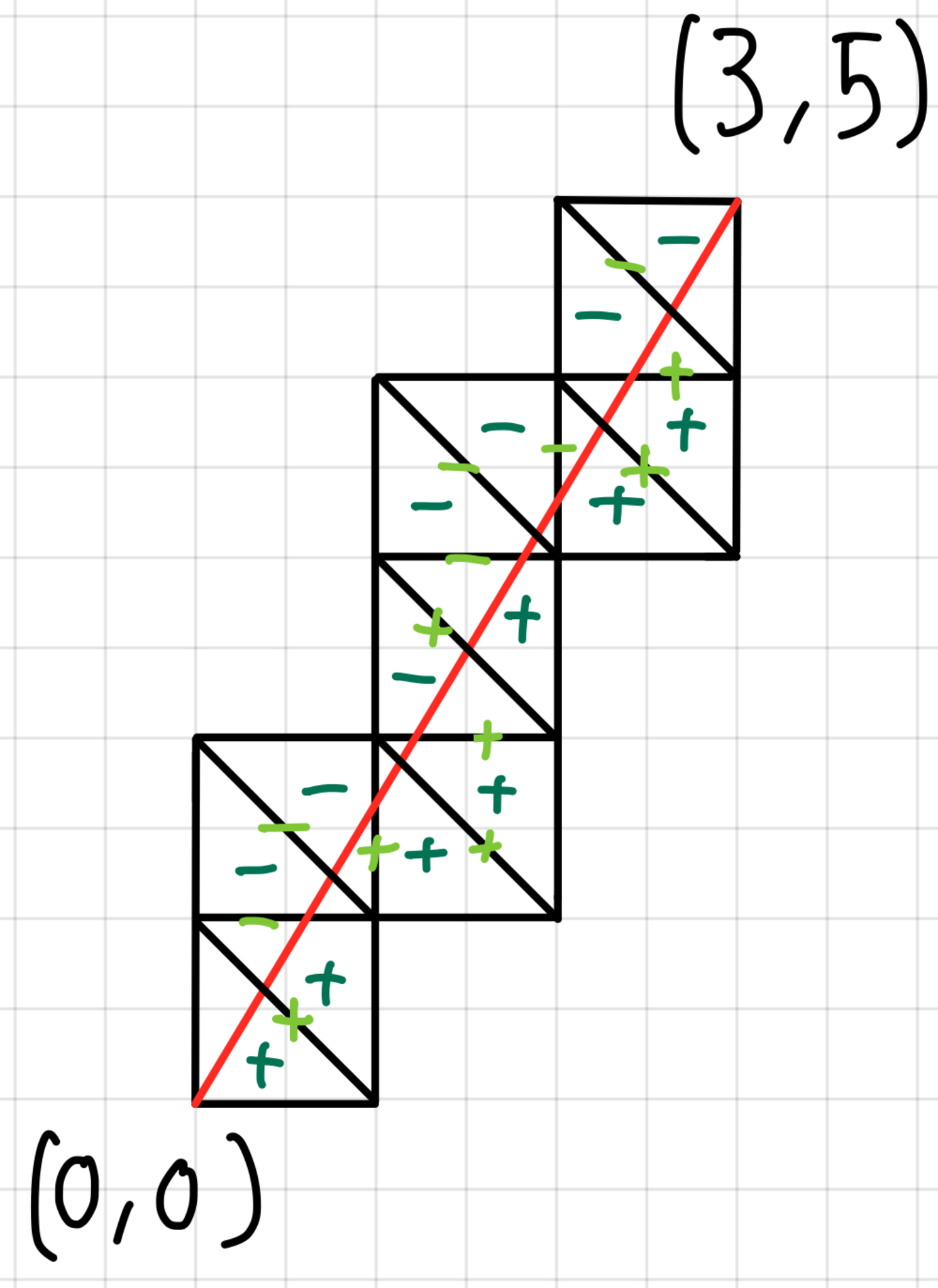既約分数5/3の例

したがって，符号の列は $(+, +, +, -, -, -, -, +, +, +, +, +, -, +, +, -, -, -, -, -, +, +, +, +, +, -, -, -)$ であり，計算する連分数は $[3, 4, 5, 1, 2, 5, 4, 3]$ となります．実際に計算するとこれは $\frac{16693}{5153}$ なので， $M_{\frac{5}{3}} = 16693$ となります．ここで， $(x, y, z) = (217, 13, 16693)$ は方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の正整数解になっているので， $16693$ は擬似マルコフ数です．

擬似マルコフ数の方も，やはりFareyトリプルツリーとの対応があることがわかります．

Fareyトリプルツリーの頂点 $(\frac{a}{b}, \frac{c}{d}, \frac{e}{f})$ に対して， $(M_{\frac{a}{b}}, M_{\frac{c}{d}}, M_{\frac{e}{f}})$ は方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の解となる（ただし $M_{\frac{0}{1}} = M_{\frac{1}{0}} = 1$ と約束する）．

特に，Fareyトリプルツリーの頂点の既約分数を全て $M_{\frac{p}{q}}$ で置き換えたツリーは次のようになり，このツリーの中央から上の部分，または中央から下の部分だけを考えると，これは擬似マルコフの木の2列目以降に一致していることがわかります（擬似マルコフの木の定義については例えばここの「名無しの木」の定義を参照してください）．
拡張された擬似マルコフの木
こちらについても，やはりマルコフの場合と同様の予想が立ちます．

擬似マルコフ数 $C$ に対して， $C = M_{\frac{p}{q}}$ を満たす1以上の既約分数 $\frac{p}{q}$ は一意的である．

ちなみに，現状ではマルコフの場合にわかっていないが擬似マルコフの場合にわかっている定理などはまだ1つもない状況です．挑戦者求む！

さらなる一般化の場合は…？

マルコフのディオファントス方程式・マルコフ数にはさらなる一般化があるという話をこの記事でしているのですが，現状では今回紹介したような既約分数から連分数を使って解を取り出せる方程式はこの記事で扱った2つの場合以外については見つかっていません．でももしかしたら僕が気づいてないだけで，他にもあるのかもしれないので探してみてください．と言うことで，今回の記事はここまでにしたいと思います．ここまで読んでくださってありがとうございました．