トポロジカル物性入門

本記事は 駒場理数豚汁カレンダー 20日目の記事です。
本日は最近僕が興味を持って勉強しているトポロジカル絶縁体/超伝導体について紹介しようと思います。

←というつもりで書いていたのですが全然間に合いませんでした。
続きは駒場祭後にこの記事に追記する or 長くなれば続編としてPhysics Lab 2026のアドカレに書こうかなと思っております。
ぜひそちらも読んでください〜
またお詫びと言ってもなんですが、豚汁を3つこの記事につけておきました。
ぜひ探してみて下さいね！

簡単な模型の設定から豊富な非自明な現象が出てくる点が物性物理の一つの魅力だと思っています。
今回の記事では、なるべく状況を簡単にし、近年流行りのトポロジカル物性についてその一端を垣間見ていただけたらと思っております。

トポロジカル絶縁体とは？

固体は大きく分けて、金属、絶縁体、半導体に分類されます。
電流を流せる金属とは異なり、通常の絶縁体は名前の通り電流を絶縁し、電気を流しません。

ところが今回のテーマであるトポロジカル絶縁体は、中身は通常の絶縁体なのに表面は金属のように電流を通す不思議な物質なのです。

通常の物理では端っこなど対して重要でなく、適当に境界条件を貸しておけば良いと思われていることが多いです。
ところが、このようなトポロジカル絶縁体を含むトポロジカル物質ではそのような従来の物理観に反し、表面が注目を浴びる新たな物理であるという興味深い現象なのです。

さらに整数/異常 量子Hall効果と呼ばれる現象では、その表面に流れる電流の流れやすさ（Hall伝導度）が整数で量子化され、試料の種類や大きさに依らないという非自明な性質を持っています。

これらの非自明な現象を陰で操っている犯人が名前にもあるとおり理論に潜むトポロジカルな性質であることを暴くことがこの記事の目標です。

今回紹介する予定の模型は全て、相互作用のない自由フェルミオンの生成消滅演算子の二次形式で書かれたHamiltonianを用いて説明できます。
豊富で非自明な現象が全てシンプルな模型から説明できてしまうことに皆さんもきっと感動していただけるでしょう。

さらにこれらの自由フェルミオンで記述されるトポロジカル絶縁体/超電導体たちは背後に綺麗な数理が隠れており、それを元にHamiltonianをある対称性でクラス分けした下で任意の次元に対し、どんなトポロジカルな性質を持てるかを調べると綺麗な周期性(Bott周期性)が現れるという面白い理論があります。
（トポロジカル周期表などと呼ばれます。）
当初はこちらについての記事を書く予定だったのですが、これだけ説明すると何だかありがたみがわかりませんし、周期表のひとマスを切り取ってみても以下に見るようにとても面白い現象が詰まっています。せっかくなので具体的な模型も見た方が愛着が湧くだろうということで2本立て(3本立て？)としました。
続きは Physics Lab 2026 のアドベントカレンダーで！

それではさっそく以下では本題に入り、まずは一番シンプルなトポロジカル絶縁体の一つであるSSH模型を用い、トポロジカルな性質であることを実際に外観します。
次に異常量子Hall効果を実際に具体的な模型を用いて再現する流れで進めていこうと思います。

SSH模型

SSH模型(Su–Schrieffer–Heeger model)とは以下のようなA,Bの２粒子がペアになり、最近接のサイトをホッピングし合う模型です。
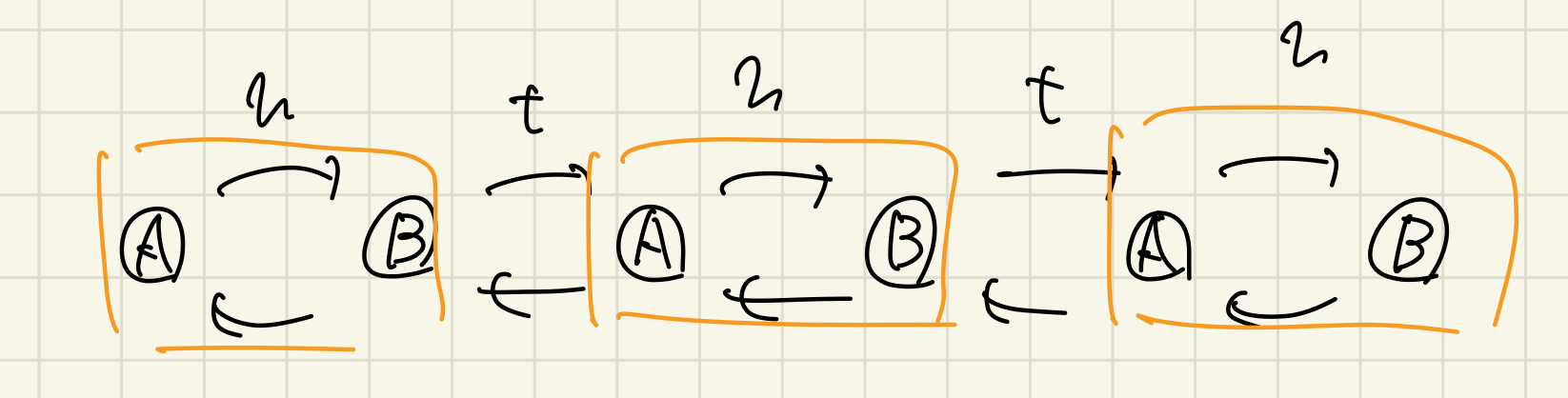SSH模型
Hamiltonianは
$\mathcal{H} = \sum_{n=1}^{L}\big[v(b^{\dagger}_n a_n+a_n^{\dagger}b_n)+t(a_{n+1}^{\dagger}b_n + b_n^{\dagger}a_{n+1})\big]$
のようにかけます。($v,t$は実数です。)
これをFourier変換すると
$\mathcal{H}(k)=\sum_{k} (a_k^{\dagger} \ b_k) \begin{eqnarray} \left( \begin{array}{cc} 0 & v+te^{ik} \\ v+te^{-ik} & 0 \end{array} \right) \end{eqnarray} \begin{pmatrix} a_k\\ b_k^{\dagger} \end{pmatrix} $
のように綺麗な形に書けます。
このBloch行列はPauli行列を用いて簡単にかけ、
$H= x\sigma_x + y\sigma_y +z\sigma_z$
を二乗すると$x^2+y^2+z^2$倍の単位行列になることから固有値が$\sqrt{x^2+y^2+z^2}$になることを用いるとエネルギー分散が
$E = \pm \sqrt{v^2 + t^2 + 2vt \cos{k} }$
と求まりギャップのある絶縁体であることがわかります。
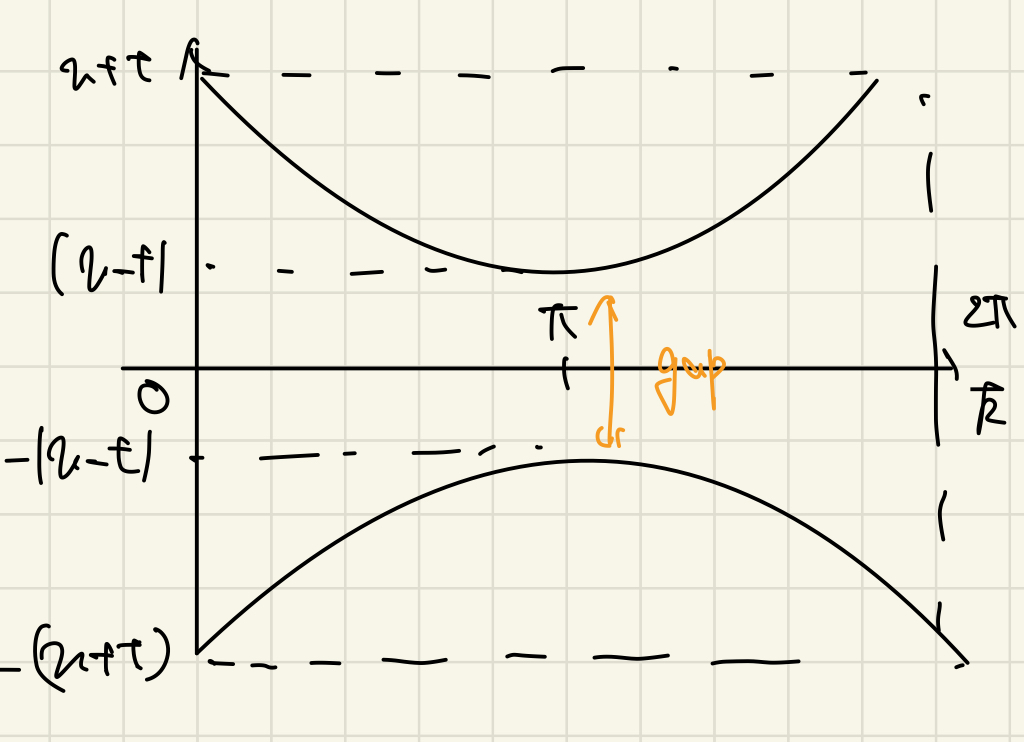バンドギャップ

この式をじっと見ると、
$$ \begin{eqnarray} \left\{ \begin{array}{l} k=0, v+t = 0 \\ k=\pi, v-t = 0 \end{array} \right. \end{eqnarray} $$
でギャップが閉じることがわかります。
そのため$v/t$を変数として相図を書くと以下のようになります。
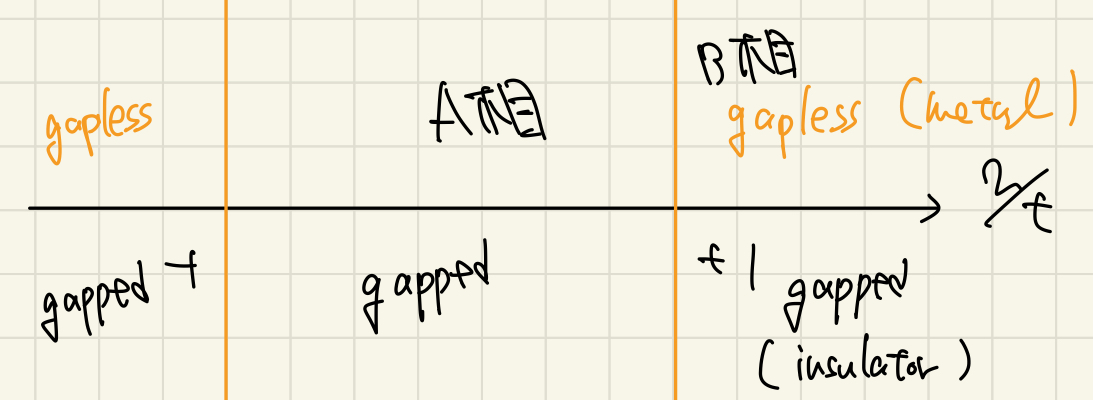相図

この相図を見るとふと素朴な疑問が浮かびます。

水や磁石などの従来の相の定義は相図の線をまたぎ相転移した際に秩序パラメタが生じ、それを用いて簡単に判別できます。
しかし今回の相を見てみると間にギャップの閉じる相転移点はあるものの、秩序パラメタが変わるような相転移は起きていません。
これら相転移によって隔たれた相の間に本質的な分類基準はあるのでしょうか？

それを考えるにあたり、まずはこの相で何か物理的な違いはあるのか見てみましょう。

唐突ですが、ぞれぞれの相でゼロモード（エネルギー固有値がゼロになる状態）について考えてみます。
ゼロモードとして
$\psi_0 = \begin{pmatrix} A_1\\ B_1\\ A_2\\ B_2\\ \vdots\\ \end{pmatrix} $
と置くと、ゼロモードの条件$\hat{H}\ket{\psi_0}=0$より漸化式がたち、ゼロモードが具体的に
$\ket{\psi_0}= C\sum_{n}(-v/t)^{n-1}a_n^{\dagger}\ket{0} $
のように書けることがわかります。
このことから

• ゼロモードは指数関数的に減衰する
  $\sum_n (-t/v)^n= e^{-n\log(t/v)}$
• 規格化できる。つまり物理的なモードとして存在できるのは$|v/t|<1$の時

であるということがわかります。
そのため、A相ではゼロモードは存在できるが、B相では存在できない。つまりA相,B相の区別に使えるのではないでしょうか？

とは言いつつも仮にゼロモードが存在できるか否かで区別ができたとしても、それが重要な性質ではなくたまたま都合のいい物理量だったとしたらあんまりおいしくはありませんよね。
ですが、実はこのゼロモードは摂動的に安定な（何かちょっとやそっとのことではびくともしない）状態であるのです。
実際に数値計算などを用いて今までの結果は確かめることができますし実験で観測もされています。

ではなぜこのように安定なのでしょうか？この奇妙なゼロモードの正体はなんなのでしょうか？

その答えは対称性にあります！
このSSH模型のHamiltonianは以下のカイラル対称性を持っています。

この対称性を持っていると以下のようにゼロモードが守られます。

このゼロモードは相転移などが起き、gapが閉じない限り勝手に増えたり減ったりすることはできません。
そのためA相,B相の間を分類する良い指標となっています。

このゼロモードの有無をより定量的に評価できないでしょうか？
先にも述べた通り、ゼロモードはギャップが閉じない限り不変です。
よってgapが閉じない限り不変な量を見つけてくれば筋が良さそうです。
Bloch Hamiltonianは
$H(k)= \begin{eqnarray} \left( \begin{array}{cc} 0 & q(k) \\ q^{\dagger}(k) & 0 \end{array} \right) \end{eqnarray} , q(k) = v+te^{ik} $
のような形をしていました。
ギャップが閉じるのはゼロ固有値が生じる$ |q| = 0$の時です。
この$q$をA相, B相で図にしてみると以下のようになっています。
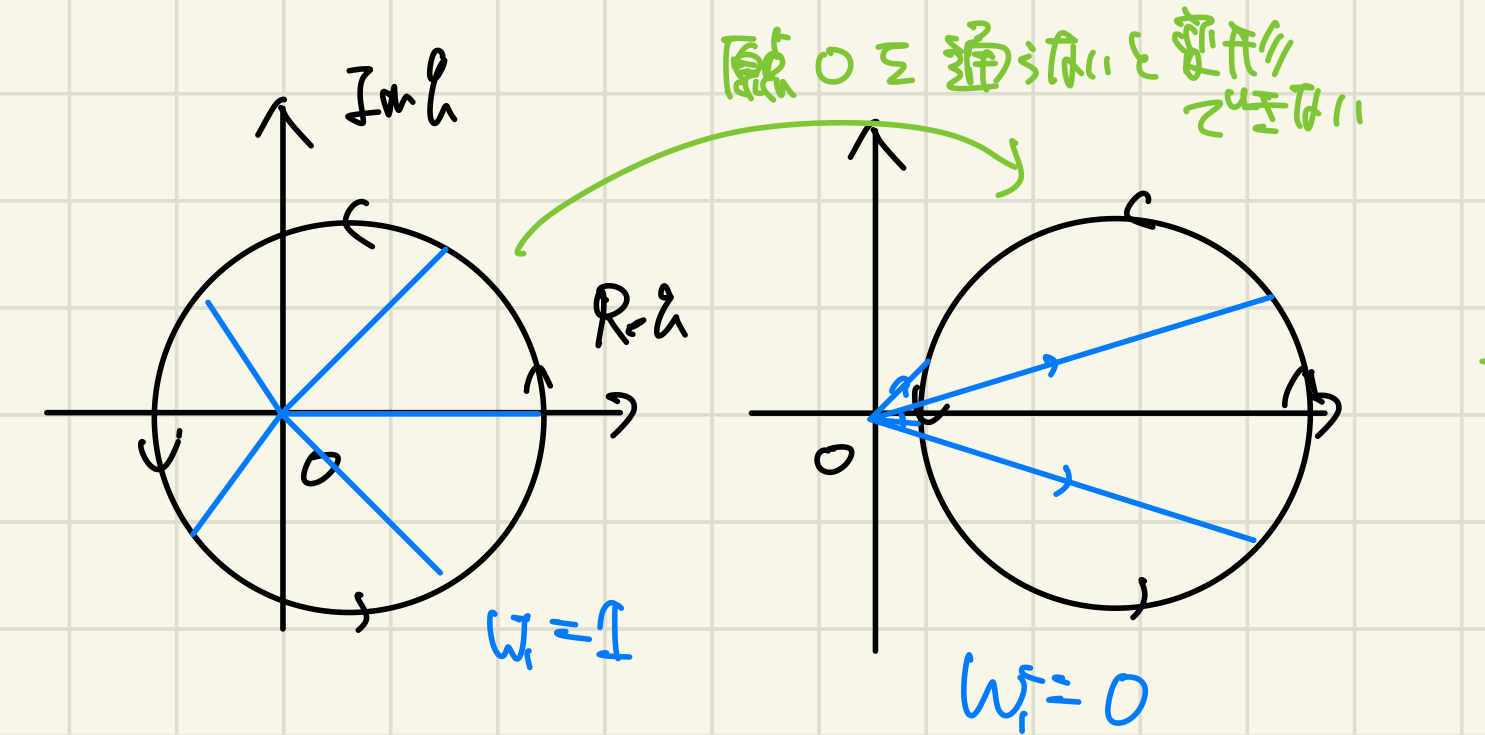q

このことから原点を含むか否かでA相, B相の区別ができることがわかります。
それを区別する幾何学的な量として巻きつき数というものがあります。

要は以下のように原点から軌跡を辿った時に何回原点を回りますか？という量になっています。
この巻きつき数は数学の言葉で言うと位相不変量になっており、トポロジカルな性質（ちょっと動かしただけでは変わらない）を持っています。
このようにgapという特異点を元にしたトポロジカルな性質が背後に隠れていたため、摂動的に安定なゼロモードが存在できていたのです。

従来の自発的対称性の破れを元にした秩序パラメタを用い特徴付けられる相とは異なる、このような相にはSPT相(Symmetry Protected Topological phase)と名前が付けられています。

この章での議論をまとめると

• SPT相にはエッジに局在したゼロモードが存在した。
• ゼロモードは対称性によって守られ摂動的に安定な性質を持つ。
• 理論が隠し持っていたトンジルカルな性質が重要な役割を果たしていた。

このような性質は他のトポロジカル絶縁体においても同様に成り立ちます。
このシンプルなSSH模型で得た直感を元により豊富な現象へと向かっていきましょう！

異常量子Hall効果

異常量子Hall効果とは？

まずは異常量子Hall効果とは何かについて説明しようと思います。
Hall効果とは物体に電場をかけ、電流が流れている時に電場と垂直な方向に磁場をかけると電場、磁場の両方に垂直な方向に電荷分布が偏ることにより起電力が生じる現象のことでした。
この時、横方向の伝導度は磁場に比例し連続的な量をとります。
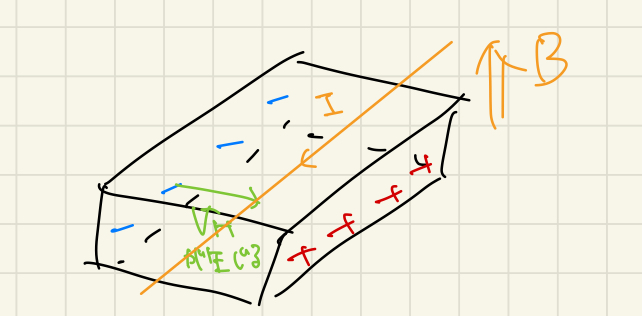Hall効果

量子Hall効果では絶縁体に対し、同様のセットアップを考えた際に、横方向の電流応答であるHall伝導度$\sigma _{xy}$
$ j_x = \sigma_{xy}E_y$
が
$\sigma_{xy}=\frac{e^2}{h}N, N \in \mathbb{Z}$
のように整数の値で量子化されます。
さらに異常量子Hall効果では磁場をかけずに同様の量子化が起こります。

今回はこの異常量子Hall効果について解説します。

Hall伝導度とChern数

なぜHall伝導度$\sigma _{xy}$は量子化されるのでしょうか？
その謎を探るために実際にHall伝導度を計算してみましょう。

y方向に電場をかけるため、それによるHamiltonianの変化を摂動とみなすと
$\ket{n}_E = \ket{n}+\sum_{m(\neq n)}\frac{\bra{m}(eEy)\ket{n}}{E_n-E_m}\ket{m}+ \cdots$
のように状態は変化します。
Hall電流（横向きの電流）は
$\braket{j_x}_E = \sum_n f(E_n)\bra{n}_E(\frac{-eEv_x}{L^2})\ket{n}_E$
のように書かれるので具体的に代入し計算すると
$\sigma_{xy}= -\frac{i\hbar e^2}{L^2}\sum_{\mathbf{k}}\sum_{n\neq m}f(E_n)\frac{\bra{n}v_x\ket{m}\bra{m}v_y\ket{n}-\bra{n}v_y\ket{m}\bra{m}v_x\ket{n}}{(E_n-E_m)^2}$
となります。（但し速度に関するHeisenbergの運動方程式を用いました。）
並進対称性があると仮定しBloch状態で展開できるとすると
$H\ket{u_{n\mathbf{k}}}=E_{n\mathbf{k}}\ket{u_{n\mathbf{k}}}$
を微分して期待値を取った関係から
$ \bra{u_{m\mathbf{k}}}v_y \ket{u_{n\mathbf{k}}} = \frac{1}{\hbar}(E_{n{\mathbf{k}}}-E_{m \mathbf{k}})\bra{u_{m\mathbf{k}}}\frac{\partial}{\partial k_{\mu}}\ket{u_{n\mathbf{k}}} $

のように速度の期待値を運動量の微分に書き換えることができます。

これを用いてHall伝導度を再び書き換えると
$\sigma_{xy}= -\frac{ie^2}{\hbar L^2} \sum_{\mathbf{k} }\sum_n f(E_{_n\mathbf{k}})\Big( \frac{\partial}{\partial k_{x}}\bra{u_{n\mathbf{k}}}\frac{\partial}{\partial k_{y}}\ket{u_{n\mathbf{k}}} -\frac{\partial}{\partial k_{y}}\bra{u_{n\mathbf{k}}}\frac{\partial}{\partial k_{x}}\ket{u_{n\mathbf{k}}} \Big)$
のように書き換えることができます。
カッコの中にある量を
$a_n(\mathbf{k})=-i\bra{u_{n\mathbf{k}}}\frac{\partial}{\partial k_{y}}\ket{u_{n\mathbf{k}}}$
と置くと、Fermi準位がギャップの間にあるとき、$\mathbf{k}$の和は波数空間全体(BZ全体)でとれば良いのでこの式は
$\sigma_{xy}=\nu \frac{e^2}{h}$
但し
$\nu = \sum_n\int_{BZ}\frac{d^2\mathbf{k}}{2\pi}\Big(\frac{\partial a_n,y}{\partial kx}-\frac{\partial a_n,x}{\partial ky}\Big)$
のように書けます。
この$a_n(\mathbf{k})$にはBerry接続、この被積分関数$\Big(\frac{\partial a_n,y}{\partial kx}-\frac{\partial a_n,x}{\partial ky}\Big)$にはBerry接続との名前がついています。

接続の意味について気になる方は、手前味噌になってしまいますが、 僕が昔書いた記事 などにやや物理の人向けの説明が載っています。

では具体的な模型を用いてこの量を計算してみましょう。
$2\times2$のBloch Hamiltonianは一般的にオフセットをすれば
$H(k) = \mathbf{R}(k_x, k_y)\cdot \mathbf{\sigma}= \begin{eqnarray} \left( \begin{array}{cc} R_z(k) & R_x(k)-iR_y(k) \\ R_x(k)+iR_y(k) & -R_z(k) \end{array} \right) \end{eqnarray} $
のように書けます。（但し$\mathbf{\sigma}$はパウリ行列です。）
SSH模型の場合は
$ \mathbf{R}= \begin{eqnarray} \left( \begin{array}{cc} v + t\cos k \\ -t\sin k \\ 0 \end{array} \right) \end{eqnarray} $
でしたが今回は
$ \mathbf{R}= \begin{eqnarray} \left( \begin{array}{cc} t\sin{k_xa} \\ t\sin{k_ya} \\ m + r\sum_{\mu = x,y}(1-\cos{k_\mu a}) \end{array} \right) \end{eqnarray} $
のように選びます。
但し$t,r>0$で$a$は格子間隔です。
先ほど同様にPauli行列で書かれた行列の固有値の公式より、これもギャップを持つ絶縁体になっていることがわかります。
この場合のBerry接続について計算してみましょう。先ほど定義したBerry接続は以下のように変数変換できます。
$a_\mu (\mathbf{k}) = -i\bra{\psi}\frac{\partial}{\partial k_\mu} \ket{\psi} =-i\frac{\partial R_a(\mathbf{k})}{\partial k_\mu}\bra{\psi}\frac{\partial}{\partial R_a(\mathbf{k})}\ket{\psi}\coloneqq \frac{\partial R_a(\mathbf{k})}{\partial k_\mu}A_a(\mathbf{k})$

これで先ほどのBerry曲率を書き換えると
$b(\mathbf{k}) = \frac{\partial a_y}{\partial k_x}-\frac{\partial a_x}{\partial k_y} = \cdots = \frac{\partial R_a(\mathbf{k})}{\partial k_x}\frac{\partial R_b(\mathbf{k})}{\partial k_y} \Big(\frac{\partial A_b}{\partial k_a}-\frac{\partial A_a}{\partial k_b}\Big)$
ここで実際に状態ベクトルとして
$\ket{\mathbf{R}}=e^{-i\psi/2} \begin{eqnarray} \left( \begin{array}{cc} e^{-i\phi/2}\cos \frac{\theta}{2} \\ e^{i\phi/2}\sin \frac{\theta}{2} \end{array} \right) \end{eqnarray} $
とおいて具体的に計算すると
$ b(\mathbf{k}) = \frac{1}{2R^3}\mathbf{R}\cdot\Big( \frac{\partial \mathbf{R}}{\partial k_x}\times \frac{\partial \mathbf{R}}{\partial k_y}\Big) $
となることがわかります。
この$\mathbf{R}$ベクトルを規格化し単位ベクトル$\hat{\mathbf{R}}$に書き換えるとHall伝導度が
$\sigma _{xy} = -\frac{e^2}{h}\int_{BZ}\frac{d^2\mathbf{k}}{4\pi}\hat{\mathbf{R}}\cdot \Big(\frac{\partial \hat{\mathbf{R}}}{\partial k_x}\times \frac{\partial \hat{\mathbf{R}}}{\partial k_y}\Big)$
のように書き表せます。
この式は何を意味しているのでしょうか？
豚汁
$\hat{\mathbf{R}}(k_x, k_y)$を端数空間上のベクトル場だと思ってみましょう。
するとHall伝導度の積分の中身は$\mathbf{R}$空間上での面積要素
$d\mathbf{S}=\big( \frac{\partial\hat{\mathbf{R}}}{\partial k_x}dk_x\big)\times\big( \frac{\partial\hat{\mathbf{R}}}{\partial k_y}dk_y\big)$
を$\hat{\mathbf{R}}$に射影した量なっていることがわかります。
$\hat{\mathbf{R}}$は規格化されており、二次元の球面上に値をとります。
つまり立体角の微小要素になっています。
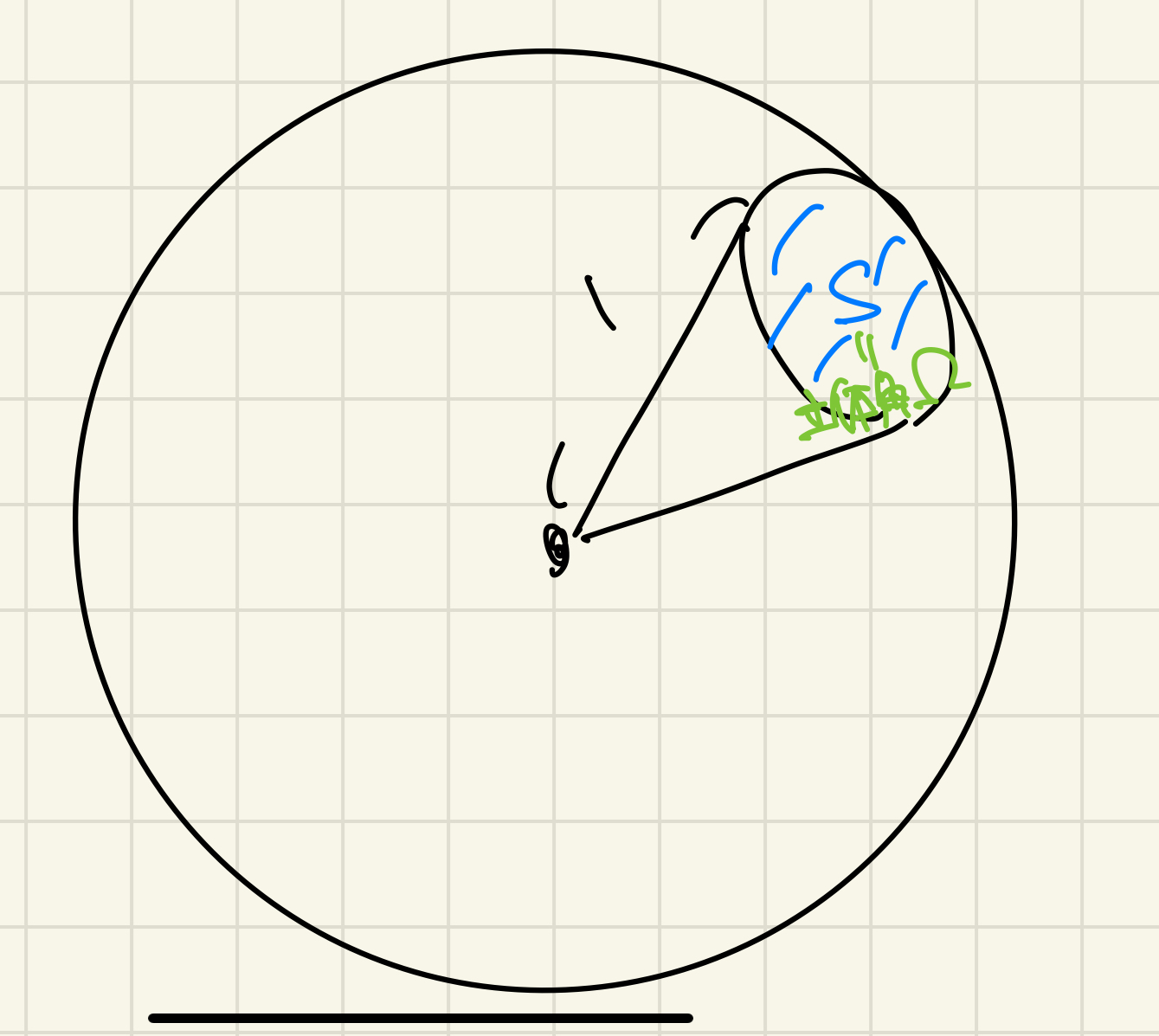立体角
少し話を戻してSSH模型を思い出してみましょう。
そこでは巻きつき数
$ W_1\coloneqq \frac{1}{2\pi}\oint_{BZ} d(\arg q(k) ) $
が位相不変量になっていました。
今回の量はまさに2次元における巻きつき数に他なりません。

この量は1次元の時に原点を何回回ったかを表していた$W_1$の素朴な拡張で、球面を何回覆ったかを表しています。
つまり離散的な量になっているはずです。

実際に模型ではどうなっているかみてみましょう！
パラメタは以下のように定義されていました。
$ \mathbf{R}= \begin{eqnarray} \left( \begin{array}{cc} t\sin{k_xa} \\ t\sin{k_ya} \\ m + r\sum_{\mu = x,y}(1-\cos{k_\mu a}) \end{array} \right) \end{eqnarray} $
まず$m>0$の時、$z$が負の値を取れないため、ベクトル場は常に上を向いています。
これじゃあ球面を覆い尽くせませんね。
なのでHall伝導度$\sigma_{xy}$はゼロです。

では$m<0$の時はどうでしょうか？
$1-\cos$の値が原点近くでは0になるため、$z$座標の値は負になります。
一方で、mの値が$-2$より大きければ端の方では符号が正になり、球面を一度覆うことがわかります。
つまり巻きつき数が非ゼロとなり、Hall伝導度が
$\sigma_{xy}= -\frac{e^2}{h}C$ (但しCは整数)
と有限の値を持つ、つまりHall電流が流れなおかつ基礎物理定数の整数倍の値をとることがわかります。
ある絶縁体に磁場はかけずに電場のみをかけ、Hall伝導度を計算すると見事整数に離散化することが説明できました。

ではこれは何により起こっているのでしょうか？
その答えはまたもやエッジに潜んでいます。

エッジ状態

先ほどはエッジにゼロモードが潜んでいました。
今回にもそのようなモードは存在するのでしょうか？

電流が流れているということはトポロジカルに非自明な状況ではバンドギャップの間に新たなバンドが生じているはずです。
先ほどの例を見ると$k$空間での原点での振る舞いが$m$の正負によりガラリと変わりました。
なんだか怪しいですね。
$k$が小さい領域を探ってみましょう。

Hamiltonianの$k$を線型近似し高次の項を無視すると$k\to -i\frac{\partial}{\partial x}$のように$k$を表現できますね。
するとHamiltonianは
$H(k)= \begin{eqnarray} \left( \begin{array}{cc} m(y) & ta (-i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}) \\ ta (-i\frac{\partial}{\partial x}+\frac{\partial}{\partial y}) & -m(y) \end{array} \right) \end{eqnarray} $
のように近似できます。
簡単のため、x方向に周期境界条件を課して境界を無くしましょう。
この時、エネルギー固有値がゼロの解として
$\exp[-\frac{1}{ta}\int^{y}dy'm(y')] \begin{eqnarray} \left( \begin{array}{cc} 1 \\ -1 \end{array} \right) \end{eqnarray} $
が存在します。
一方x方向にはエッジはないので線型分散$E=-tak_x$が持てるとしましょう。
するとyの境界に局在したエッジ状態
$ \begin{eqnarray} \left( \begin{array}{cc} u \\ v \end{array} \right) \end{eqnarray} = A\exp[ik_x x-\frac{1}{ta}\int^y dy'm(y') ] \begin{pmatrix} 1\\-1 \end{pmatrix} $
が解として存在します。
これはバンドの間に以下のようなエッジモードによるスペクトルが現れます。
これこそがHall電流の原因です。
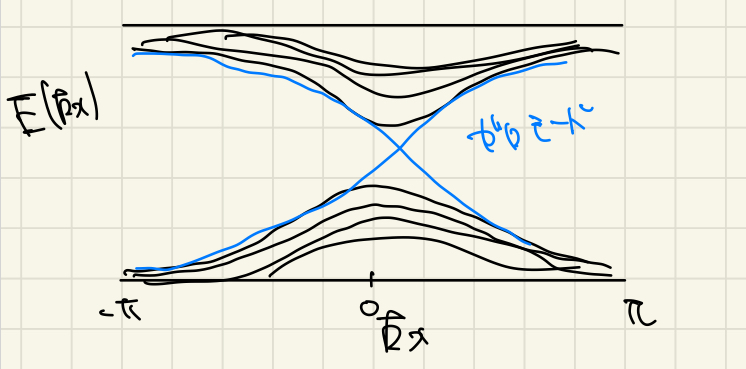エッジ状態の様子（汚すぎてごめんなさい）

まとめ

以上の話をまとめましょう。
はじめに1次元のトポロジカル絶縁体としてSSH模型をみました。
そこでは、相がトポロジカル不変量によって分類されることや、エッジに安定なゼロモードが生じることを見ました。
次に2次元の例として量子異常Hall効果を見ました。
そこでも同様にエッジにゼロモードが生じ、それにはトポロジカルな性質が一役買っていました。
さらに2次元の場合は空間次元が増えたことによりそのゼロモードが自由度を持ち、それが非自明で有用な量子Hall効果を生んでいるということがわかりました。

以上がトポロジカル絶縁体の紹介でした。
少しでも興味を持っていただければ幸いです。
最後まで読んでいただきありがとうございました！