∫ [ x*sin(x)/(1+x^2) dx, 0 -> ∞ ] を複素積分で求める

はじめに

　最初は計算ミスしたり, WolframAlphaにかけてみたらずっと敬遠してきた系の積分だったりしたのでめちゃくちゃ弱気だったんですが, 計算ミスに気づいたら求まっちゃったのでめちゃくちゃ嬉しかったです.
　複素積分に関してはまだまだ未熟なので今回の積分はいい勉強になったと思います.
　そして複素積分で解くというヒント以外は, 複素積分のやり方を本でカンニングしたぐらいでほとんど自力なので自分でした計算として記事にしようと思いました.

問題

この積分を$I$とします.

解答

以下の図の積分路$C$に対して次のような複素積分を考えます.
ABCとDEFはそれぞれ半径$R, r$の半円です.
$$\int_C\frac{ze^{iz}}{1+z^2}dz$$

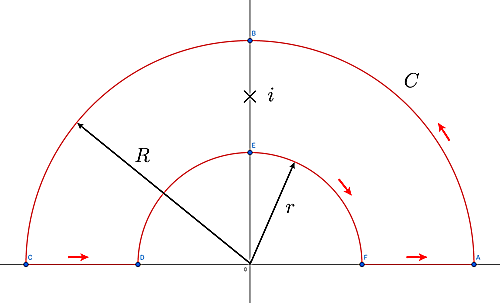積分路C

積分経路を四つの部分に分けて積分します. (☆)
$$\int_C\frac{ze^{iz}}{1+z^2}dz=\int_r^R\frac{xe^{ix}}{1+x^2}dx+\int_{ABC}\frac{ze^{iz}}{1+z^2}dz+\int_{-R}^{-r}\frac{xe^{ix}}{1+x^2}dx+\int_{DEF}\frac{ze^{iz}}{1+z^2}dz$$
(1) 左辺の積分
閉曲線$C$の$z=i$を除いた周と内部において被積分関数は正則であるから,
$$\int_C\frac{ze^{iz}}{1+z^2}dz=\int_C\frac{\frac{ze^{iz}}{z+i}}{z-i}dz=2\pi i\cdot\frac{ie^{i^2}}{i+i}=\frac{i\pi}{e}$$

2. 右辺の積分①
   $$\int_{ABC}\frac{ze^{iz}}{1+z^2}dz$$
   $z=R(\cos\theta +i\sin\theta)=Re^{i\theta}\quad (0\leq\theta\leq\pi)$と置換すると,
   $$=\int_{ABC}\frac{Re^{i\theta}e^{iR(\cos\theta +i\sin\theta)}}{1+R^2e^{2i\theta}}d\theta$$
   ここで,
   \begin{align*} \left|\int_{ABC}\frac{Re^{i\theta}e^{iR(\cos\theta +i\sin\theta)}}{1+R^2e^{2i\theta}}d\theta\right|&\leq\int_{ABC}\left|\frac{Re^{i\theta}e^{iR(\cos\theta +i\sin\theta)}}{1+R^2e^{2i\theta}}\right|d\theta\\ &=\int_{ABC}\frac{|R||e^{i\theta}||e^{iR\cos\theta}||e^{-R\sin\theta}|}{|1+R^2e^{2i\theta}|}d\theta=\int_0^\pi \frac{Re^{-R\sin\theta}}{|1+R^2e^{2i\theta}|}d\theta\\ &=\frac{1}{R}\int_0^\pi\frac{e^{-R\sin\theta}}{\left|\frac{1}{R}+e^{2i\theta}\right|}d\theta\\ &\leq\frac{1}{R}\int_0^\pi e^{-R\sin\theta}d\theta\to 0\quad(R\to \infty) \end{align*}

※ 右辺は線積分であることに注意します.
(3) 右辺の積分②
$$\int_{DEF}\frac{ze^{iz}}{1+z^2}dz$$
(2)と同じく$z=r(\cos\theta +i\sin\theta)=re^{i\theta}\quad (0\leq\theta\leq\pi)$と置換すると,
$$=\int_\pi^0\frac{re^{i\theta}e^{ir(\cos\theta +i\sin\theta)}}{1+r^2e^{2i\theta}}d\theta$$
となり, これも同様に$r\to0$のとき, (与式)$\to0$となります.
(4) 右辺の積分③
$$\int_r^R\frac{xe^{ix}}{1+x^2}dx+\int_{-R}^{-r}\frac{xe^{ix}}{1+x^2}dx$$
二項目のみ$x\longmapsto -x$と置換すると
$$=\int_r^R\frac{xe^{ix}}{1+x^2}dx-\int_R^r\frac{-xe^{-ix}}{1+x^2}dx=\int_r^R\frac{xe^{ix}}{1+x^2}dx-\int_r^R\frac{xe^{-ix}}{1+x^2}dx$$
$e^{ix}-e^{-ix}=2i\sin x$だから,
$$=2i\int_r^R\frac{x\sin x}{1+x^2}dx$$
ここでようやく求めたい積分が出てきましたね.

よって(1)～(4)より, (☆)は$R\to\infty,\ r\to0$とすると
\begin{align*} \int_C\frac{ze^{iz}}{1+z^2}dz&=0+0+2i\int_0^\infty\frac{x\sin x}{1+x^2}dx\\ 2iI&=\frac{i\pi}{e}\\ I&=\frac{\pi}{2e} \end{align*}