確率と面積の関係
確率と面積には双方向に密接な関わりがあり、高校数学範囲であってもそのことを理解することができる。
確率→面積
まずは確率を用いて面積を求める方法の例を挙げてみる。モンテカルロ法は広義には乱数を使ってシミュレーションを行う手法全体のことを指すが、ここでは求積に用いるモンテカルロ法について扱う。
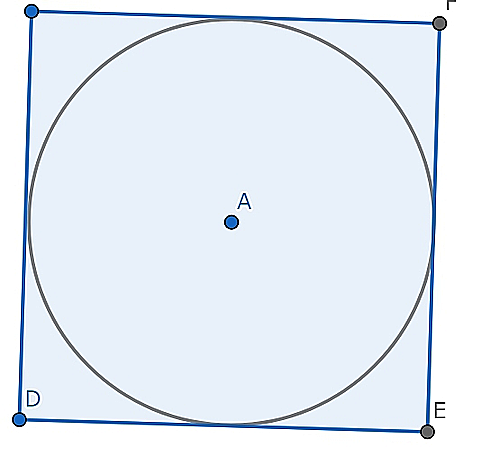モンテカルロ法
この図のように、円に外接する正方形を用意する。
この正方形内に無作為に点を打ち、打った点の総数と円内に入った点の数を比較して、以下のように求める。
$(円の面積)=(正方形の面積)\times \cfrac{(円内に入った点の数)}{(打った点の総数)}$
つまり、打った点が円内に入る確率が正方形と円の面積の比になるというわけだ。
モンテカルロ法を使うからには円周率の値を未知とすることがほとんどだが、必ずしも外接する正方形を用意する必要はなく、円を包含する、面積が既知な図形を用意できればよい。
面積→確率
まずこの例を考えてみよう。
(問) 領域$D:y\leqq -x+1,x\geqq 0,y\geqq 0$内に点を無作為に打つとき、領域$E:x\leqq \cfrac{1}{2},y\leqq \cfrac{1}{2}$内に点がある確率を求めよ。
モンテカルロ法の考え方を逆に使うと、この例は次の考え方によって解ける。
$(求める確率)=\cfrac{(領域E内に入った点の数)}{(打った点の総数)}=\cfrac{(領域D\cap Eの面積)}{(領域Dの面積)}$
このことを用いると、領域$D\cap E$の面積は$\cfrac{1}{4},$領域$D$の面積は$\cfrac{1}{2}$であるので求める確率は$\cfrac{1}{2}$であることがわかる。
これは、事象の数が数えられない場合に確率を求めたいときに使える。
(問) 実数$x,y$は$x^2+y^2\leqq 1$を満たすとする。この条件を満たす組$(x,y)$を無作為に選んだとき、$(x,y)$が$|x|+|y|\leqq 1$を満たす確率を求めよ。
これも例1を理解できれば難しくはなく、それぞれの領域の面積を考えてやればいい。領域$D,E$を$D=\{ (x,y)|x^2+y^2\leqq 1\} ,E=\{ (x,y)||x|+|y|\leqq 1\}$とすると、$E\subset D$であり、それぞれの面積は$\pi ,2$なので求める確率は$\cfrac{2}{\pi}$であると求まる。