ハンター試験四次試験って何人まで合格できるの？

HUNTER×HUNTER

皆さん，HUNTER×HUNTER [1] は履修済みですか？主人公のゴンが仲間と共に切磋琢磨する作品です（ざっくり）．この世界ではハンターと呼ばれる職業がみんなの憧れとなっています．ハンターとは，怪物・財宝・賞金首など，稀少な事物を追求することに生涯をかける人々のことです．名乗るだけなら自由ですが，ハンターライセンスという資格を取得することもできます．この資格を取得した人はプロハンターと呼ばれ，交通機関・公共機関を自由に使えたり，一般には立ち入り禁止の場所には入れたりと，さまざまな特権が得られます．ハンターライセンスを取得するための試験はハンター試験を呼ばれます．ハンターはとても危険な職業なので，厳しい試験を潜り抜けたものだけが合格できます．合格率は数万分の一とのことです．

ハンター試験四次試験

ゴンがハンター試験を受けたときには五次試験までありました．例えば，四次試験の内容は以下です．

• 各参加者には番号が書かれたプレートが割り振られる
• 各参加者には自身とは異なる番号（ターゲット）が伝えられる
• 一定期間の間，参加者は互いのプレートの取り合いをする
• 最終的に６点分のプレートを持っていた参加者が合格
• プレートの点数は以下の通り
• 自分のプレート：３点
• ターゲットのプレート：３点
• その他のプレート：１点

参加者の総合的な実力が図れる良い試験内容ですよね．

疑問

私は最適化とかアルゴリズムが好きなので，自然と次の疑問が湧いてきました．

「これって，何人まで合格できるんだろう」

直感的に一番効率的なのは，ターゲットのプレートを取った人が合格，それ以外は不合格で，参加者の半数が最大値なのかなと思いました．でも，プレートを取られた人にもまだ可能性はあるし，ターゲットの割り当て方によってはターゲット外ｘ３人分を取った方が効率的なのでは，とも思い，自明ではない気がしてきました．

ということで，本記事では，四次試験の合格者数の最大値を調べてみました．ただ，ゴンが受けた四次試験では，ターゲットの割り当てが分からない人もいました．なので，本記事ではターゲットの割り当てが所与であるときの一般的な話をします．

なんで急にそんなこと気になってんの？

さっきアニメ見てたからです．

合格者数の最大化

素直に考えれば，まずは自身＋ターゲットｘ１の合格者をたくさん埋め，次に余った参加者から自身＋ターゲット外ｘ３の合格者を埋め，最後にターゲット外ｘ６を埋める，が効率的に合格者数を増やせそうです．

まず，ターゲットの割り当て方の特徴を見てみましょう．その特徴を整理するために，以下のグラフ（ターゲットグラフ）を考えます．

• 頂点：参加者
• 有向辺：参加者$i$→参加者$i$のターゲット$j$

このとき，ターゲットグラフは「複数のサイクルから構成される」という性質を持ちます．なぜなら，各参加者のターゲットは一人（頂点$i$から出る辺は一つのみ）であり，各参加者をターゲットとする人も一人（頂点$j$に入る辺も一つのみ）だからです．よく考えてみると，単純な構造でした．

図１

まずは自身＋ターゲットｘ１の合格者で埋めていきます．参加者$i$の頂点から，参加者$i$が奪ったプレートの持ち主$j$の頂点に，ターゲットグラフの辺とは別の種類の辺を張ることで，プレートの割り当てを表します．ターゲットグラフはサイクルの構造を持つので，サイクル内で交互に奪う・奪われるの関係を作ると，合格者数を最大化できます．このとき，偶数個の頂点を持つサイクルではプレートを奪っても奪われてもいない頂点はなく，奇数個の頂点を持つサイクルではそのような頂点が一つ余ります．これらの余りの頂点はそれぞれターゲットの関係にないので，これらの頂点から自身＋ターゲットｘ１の合格者は作れません．

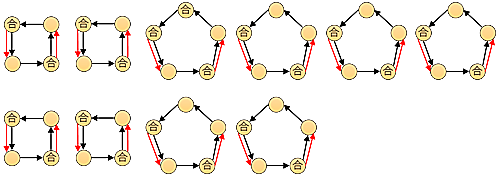図２

次に，自身ｘターゲット外ｘ３の合格者で埋めます．プレートを奪われていない参加者で，まだ合格していないのは，上記で余った頂点です．これらの頂点を４つごとにまとめ，各グループで１人が別の三人のプレートを奪えば，合格者を作れます．このとき，４人ごとにグループを作るので，グループを作れない余りの頂点は三つ以下です．

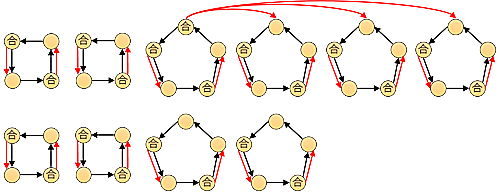図３

最後に，ターゲット外ｘ６の合格者で埋めます．ここが，プレートを奪われてしまった人のチャンスです．しかし，プレートを奪われておらず，まだ合格していない人は高々３人しかいないので，このパターンでは合格者は作れません．

まとめると，以上の割り当ての合格者数は以下で計算できます．ここで，$n_\text{even}$は偶数個のサイクルの数，$n_\text{odd}$は奇数個のサイクルの数，$m_i$は奇数のサイクル$i$の頂点数です．サイクルがすべて偶数のとき，最大値は参加者の半数になるので，最初の直感通りですね．

\begin{align} \frac{n_\text{even}}{2} + \sum_{i=0}^{n_{\text{odd}}} \frac{m_i - 1}{2} + \lfloor \frac{n_{odd}}{4} \rfloor \end{align}

ここから，以上の割り当てだと合格者数が最大であることを示したかったのですが，書いているうちに自信が無くなってしまいました．ひとまず，今回は合格者数が多くなる一例のご紹介のみとなります．．．直感的には，ターゲットグラフがサイクルの構造を持つことにより，自身＋ターゲットｘ１の合格者を崩しても，合格者は増やせない，という風に感じています．

一般化

いざ私がハンター試験に参加することになった際に，合格者数の最大値を計算できるように，一般化してプログラムにしておきます．あくまで参考値ですが，自分よりも強そうな人の数が最大値よりも多ければ，あきらめがつきますので．

一般化した四次試験は，以下のようになるかと思います．

• 参加者$i$が参加者$j$のプレートを取ったら$a_{ij}$点
• 取得プレートの合計点数が$m$点以上であれば合格

これを整数計画問題で定式化します．

\begin{align} \begin{matrix} \text{maximize} && \sum_{i} z_i && \\ \text{subject to} && \sum_{j} x_{ji} = 1 && \forall i \\ && y_i = \sum_j a_{ij} x_{ij} && \forall i \\ && z_i \leq y_i / m && \forall i \\ && x_{ij} \in \{ 0, 1 \} && \forall i, j \\ && y_i \in \mathbb{R} && \forall i \\ && z_i \in \{ 0, 1 \} && \forall i \end{matrix} \end{align}

変数と制約はそれぞれ以下を意味します．

• 変数$x_i$：参加者$i$が参加者$j$のプレートを取ったかのフラグ
• 変数$y_i$：参加者$i$の点数の合計
• 変数$z_i$：参加者$i$が合格かのフラグ
• 目的関数$\sum_{i} z_i$：合格者の合計数
• 制約$\sum_{j} x_{ji} = 1$：参加者のプレートは一枚のみ
• 制約$y_i = \sum_j a_{ij} x_{ij}$：点数の合計
• 制約$z_i \leq y_i / m$：点数が$y_i \geq m$の場合のみ$z_i$が発火(1)可能

これをpythonのライブラリpulpで解くプログラムが以下です．

      import pulp
def solve(A, m):
    # n：参加者数
    # A：nxn行列，A[i, j]は参加者iが参加者jのプレートを取った時の得点
    # m：合格の得点ライン

    n = A.shape[0]

    # 問題を作成
    prb = pulp.LpProblem("HxH", pulp.LpMaximize)

    # 取得プレートフラグ
    x = [ [ pulp.LpVariable("x_" + str(i) + "_" + str(j), cat=pulp.LpBinary) for j in range(n) ] for i in range(n) ]

    # プレート重み合計
    y = [ pulp.LpVariable("y_" + str(i)) for i in range(n) ]

    # 合格フラグ
    z = [ pulp.LpVariable("z_" + str(i), cat=pulp.LpBinary) for i in range(n) ]

    # プレートは一人一枚
    for i in range(n):
        prb += pulp.lpSum([ x[j][i] for j in range(n) ]) == 1

    # プレート重み合計
    for i in range(n):
        prb += y[i] == pulp.lpSum([A[i, j] * x[i][j] for j in range(n)]) 

    # 合格フラグ
    for i in range(n):
        prb += m * z[i] <= y[i]

    # 合格者数の最大化
    prb += pulp.lpSum(z)

    # 実行
    prb.solve()

    return prb
    

これで安心です．

最後に

くだらないことを記事にしてすいませんでした．

引用

1. HUNTER×HUNTERのwikipedia： https://ja.wikipedia.org/wiki/HUNTER%C3%97HUNTER#%E3%83%8F%E3%83%B3%E3%82%BF%E3%83%BC