円状に帯電する電荷がつくる電場
円状に帯電する電荷が作る電場について考える。簡単のため円の中心軸上の電場についてについてみる。読みやすくするため、文字の細かな定義は察してください。
実直に計算する場合
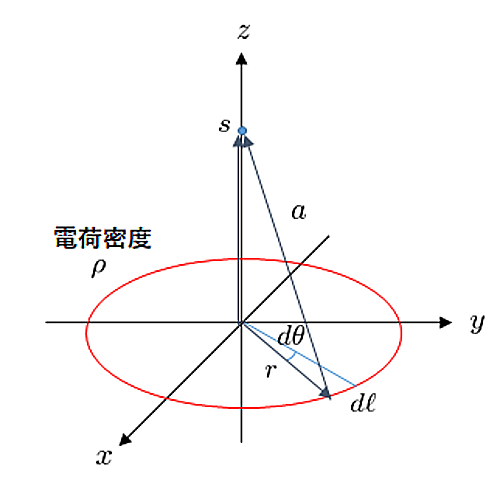 円形電荷
円形電荷
図のように赤線のところに電荷が円状に帯電しており、電荷線密度$\rho$、円の半径を$r$、考える点を$s$、円から点$s$までの距離を$a=\sqrt{r^2+s^2}$とする。点$s$で作る電場は定義から、\begin{align}
\boldsymbol{E} = \int_C\frac{\rho}{4 \pi \varepsilon_0}\frac{\boldsymbol{a}}{a^3}d\ell
\end{align}と書ける。積分領域$C$は今見ている円(赤い部分)である。今、図より\begin{align}
\boldsymbol{s}
= \left(
\begin{array}{ccc}
0\\
0\\
s
\end{array}
\right),
\boldsymbol{r}
= \left(
\begin{array}{ccc}
x\\
y\\
0
\end{array}
\right)
\end{align}とすると、\begin{eqnarray}
\boldsymbol{a} = \boldsymbol{s} -\boldsymbol{r}
= \left(
\begin{array}{ccc}
-x\\
-y\\
s
\end{array}
\right)
\end{eqnarray}であり、\begin{align}
d\ell = rd\theta
\end{align}である。これより、電場の成分それぞれは、$x=r\cos\theta$、$y=r\sin\theta$を使って、\begin{align}
E_x &= \frac{r\rho}{4 \pi \varepsilon_0 a^3}\int_0^{2\pi}(-\cos\theta)d\theta=0,\\\\
E_y &= \frac{r\rho}{4 \pi \varepsilon_0 a^3}\int_0^{2\pi}(-\sin\theta)d\theta=0,\\\\
E_z &= \frac{r\rho s}{4 \pi \varepsilon_0 a^3}\int_0^{2\pi}d\theta=\frac{r\rho s}{2\varepsilon_0 a^3}
\end{align}となる。$E_x$、$E_y$の積分について$\sin\theta$、$\cos\theta$の1周期分の積分なので$0$。$E_z$の積分部分は$2\pi$なので、上記のように書ける。
対称性を使う
上記の方法は積分の計算練習として扱えればよい。問題集や参考書等でよく見かけるのはこちらの方法であろう。
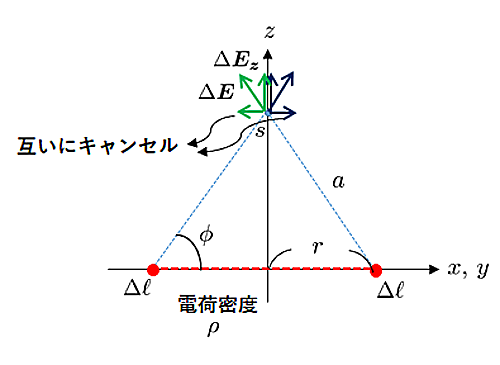 円形電荷2
円形電荷2
先ほどの図を横から見たら上図のようになる。図のように点対称な部分2点を見ると(見る線分を$\Delta \ell$とする)、点$s$で作られる電場は、$z$軸に垂直な成分はキャンセルされ、$z$方向のみ生き残る。片側の点が作る電場の$z$成分は\begin{align}
\Delta E_z = \Delta E\sin\phi
\end{align}となる。ここで$\sin\phi$は定数で、図より、\begin{align}
\sin\phi = \frac{s}{a}
\end{align}であり、また\begin{align}
\Delta E=\frac{\rho \Delta \ell}{4 \pi \varepsilon_0}\frac{1}{a^2}
\end{align}なので、\begin{align}
\Delta E_z=\frac{\rho \Delta \ell}{4 \pi \varepsilon_0}\frac{s}{a^3}
\end{align}となる。またもう片方が作る電場も同じ大きさなので両者が作る電場は\begin{align}
2\Delta E_z=\frac{\rho \Delta \ell}{2 \pi \varepsilon_0}\frac{s}{a^3}
\end{align}である。$\Delta\ell$を$d\ell$として積分をすれば良いが、注意するのは2カ所同時に見たので半周分の積分で良いということである。つまり、\begin{align}
E_z=\int_{C/2}2d{E_z}=\int_{C/2}\frac{\rho d\ell}{2 \pi \varepsilon_0}\frac{s}{a^3}=\frac{\rho}{2 \pi \varepsilon_0}\frac{s}{a^3}\int_{C/2} d\ell=\frac{\rho}{2 \pi \varepsilon_0}\frac{s}{a^3}\cdot \pi r =\frac{r\rho s}{2\varepsilon_0 a^3}
\end{align}
となる。当然だが、これらの結果は上でやった方法と一致している。物理的に大事なのは対称性を使うと簡単にできるということ、教育的にはどんな方法でも解けるようになることと思い、両者の解法を記事にしてみた。
