Haskellの魅力

リスト

リストの基本

Haskellのリストはほかの言語と同じように定義することができる.

      > a = [1,2,3]
    

新しい要素の追加は次のように行う.

      > 1:[2,3]
[1,2,3]
    

n番目の値を取得するには演算子を使う.

      > [1,2,3] !! 1
2
    

リストを結合するには++演算子を使う.

      > [1,2,3] ++ [4,5,6]
[1,2,3,4,5,6]
    

また,文字列型(String)は文字型(Char)とリスト型([])

を使って定義される.

      > :info String type String = [Char]    -- Defined in ‘GHC.Base’
    

つまり文字列に対しリストと同じような操作が可能となる.

      > a = "University"
> b = 'Y':'a':'m':'a':'g':'u':'c':'h':'i':a
> b
"YamaguchiUniversity"
> b !! 0
'Y'
> ['Y','a','m','a','g','u','c','h','i'] ++ a
"YamaguchiUniversity"
    

遅延評価

ここからが私の思うHaskellの優れた点であるが$1$から$100$までの整数の列を定義する時,Pythonではリスト内包表記を用い次のように書く.

      a = [i + 1 for i range(100)]
    

c言語ならば次のように書かれる

      int a[100];
for (int i = 0; i < 100; ++i) {
a[i] = i + 1;
}
    

しかし,Haskellならば次のように書くことが可能となる.

      a = [1 .. 100]
    

このような書き方は数学において成される書き方とよく似ている.例として$1$から$100$までの自然数の集合は以下のように表現される. $$A = \{1,\dots,100\}$$a = [1 .. 100]と言う書き方は数学に触れているならば,すぐに受け入れられるだろう.また,他の言語と比べてコードが短くて済む点もHaskellが優れている点だと思う. 数学では自然数の集合を$N$と表し,書き下すと次のように表される.
$$N = \{1,2,3,\dots\}$$これをプログラムで表現するとなるとなかなか難しいものがある.しかしHaskellならば実に簡単にこれを表現できる仕組みがある.

      >n = [1 ..]
    

このようにリストを定義してもエラーは帰ってこない.これはHaskellが必要になるまで値を評価しない遅延評価という仕組みを用いてあるからである.

試しにnの中身を表示させてみる.

      > n
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,
23,24,25,26,27，28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51，52,53,54,55,56,57,58,59,60,
61,62,63,64,65,66,67,68,69,70,71,72,73,74,75，76,77,78,79,
80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,
99，100,101,102,103,104,105,106,107,108,109,110,111,112,113,
114,115,116,117，118,119,120,121,122,123,124,125,126,127,
128,129,130,131,132,133,134,135,

(実際にはこの後も数字は続いて無限ループに入る.)
    

フィボナッチ数列が入ったリストも$1$行で定義ができる.

      > f = map (\x -> (1 / (sqrt 5)) * (((1 + (sqrt 5)) / 2) ^ x
- ((1 - (sqrt 5)) / 2) ^ x)) n
> f
[1.0,1.0,2.0,3.0,5.0,8.0,13.0,21.0,34.0,55.0,89.0,
    

この遅延評価を扱えるのもHaskellの優れている点だと思う.

x:xs構文

あるリストを引数にもつ関数を定義するときにHaskellは次のような構文が許されている.

      mySum (x:xs) = if length xs == 0
then x else x + mySum xs
    

注目すべきは関数mySumの引数にあるx:xsである.Haskellには
forやwhileといった繰り返しの表現が存在しないので,再帰がよく用いられる.そういった場合,引数にくるリストを先頭の要素とその後ろに続くリストに分けることができると都合がいい場合が多く存在する.Pythonでfor

文はリストの要素を$1$つ$1$つ変数に代入しながら繰り返しを行う,この操作とHaskellの
x:xsという表現はよく似ている.

再帰

再帰の基本

Haskellには再帰と呼ばれる構文がある.再帰はHaskellだけの特別な構文というほどのものではなくJavaやC#,Python,javascript,などでも再帰構文が用意されている.しかし,Haskellにはforやwhileといった繰り返しの表現が存在しないので,Haskellで繰り返し操作を行うには,必ず再帰構文を用いることとなる.一見不便に見えるが,再帰はHaskellの関数指向との相性がよく,関数を漸化式のように記述できるので,数学に触れていると再帰のほうが自然に見えてくると思う.

例として$n$番目のフィボナッチ数を返す関数を定義する.

      f 1 = 1
f 2 = 1
f n = f (n - 1) + f (n - 2)
    

ガード

再帰関数を定義するとき便利なガードと呼ばれる構文を紹介する.

ある関数が数学において次のように定義されているとする. $$f(x) = \begin{cases} 1 \ (x \mbox{偶数})\\ 0 \ (x \mbox{奇数}) \end{cases}$$これと同等の関数をHaskellで定義するならば次の様に表現される

      f n | even(n) = 1
    | odd(n)  = 0
    

この表現もまた数学に触れているのならば理解に難くない表現と思われる.

先ほどの再帰と組み合わせて,コラッツ列を表示するプログラムを考えると,次のようになる.

      c 1 = 1 : []
c n | even n = n : c(div n 2)
| odd n  = n : c(3 * n + 1)
    

高級関数

ラムダ関数

Haskellのロゴマークを見てほしい. Haskell

このロゴはギリシャ文字の$\lambda$を模している.つまりロゴにするほど開発者にとって$\lambda$は重要だったことが分かる.

一般のコンピューターでは$\lambda$の入力は簡単ではないので,プログラム上では$\lambda$の代わりに\が用いられる.

では,ラムダ関数とは何者だろうか,ずばりラムダ関数とは名前のない関数のことで，名前を定義するほどでもない関数を定義するのに優れている.

具体的には次のように名前のない即席の関数として用いられる.

      > (\x -> x ^ 2) 3
9
> (\x -> "a " ++ x) "pen"
"a pen"
    

然して重要とも便利とも感じられないかもしれないが,高級関数などを用いるときにその威力を発揮する.

処理の一般化

関数指向言語の思想は,“全ては関数である.”である.Haskellは変数に再代入することができない,つまりHaskellにおける変数とはもはや数学における定数であり,Haskellに言わせると“a = 0とは$a(x) = 0$と同じ定数関数である.”ということなのである.逆に言えば,関数も他のリストや数値といったデータの$1$種と考えられる.つまり,関数を引数に持つ関数を定義したり,関数を返す関数を定義することも可能ということとなる.

このことがどう便利なのか考える.

      f [] = []
f (x:xs) = ("a " ++ x) : f (xs)
g [] = []
g (x:xs) = x ^ 2 : g (xs)
    

fは文字列の列を受け取り,各文字列の先頭にa を追加する関数，gは数字の列を受け取り,各数字を$2$乗する関数である.このとき注目してほしいのは両関数とも再帰の構造としては全く同じもので,リストに適用させる関数が異なるものとなっている点である.このことを,一般化する関数こそ高級関数と呼ばれるものである.

      mMap f [] = []
mMap f (x:xs) = f x : mMap f xs
    

mMap関数は関数とリストの$2$つの引数を取る再帰関数である.この関数で先ほどのfとgは一般化されている.

つまり,高級関数を用いることで,処理を一般化することができる.このことは,プログラムの長さを削減するのにかなり役に立つ,また先のプログラムでは再帰をその都度考えてプログラミングをしなくてはいけなかったが,一度mMapのような関数を定義しておけば,fとgは次のように書ける.

      f = mMap (\x -> "a " ++ x)
g = mMap (\x -> x ^ 2)
    

かなり短く簡潔に記述できたと思う.ここで先ほど紹介したラムダ関数が登場している.

高級関数に関数を代入するときに,ラムダ関数を用いることで余計な関数を定義しないで済むのだ. 因みに今回定義したmMap関数はHaskellに初めからmapという関数として定義されているので,使いたい場合新たに定義しなくともよい.

代数的構造

モノイド

Haskellでは半群やモノイドといった基本的な代数的構造が標準ライブラリでサポートされているimport Data.Monoidと$1$行記述することで,Haskellでモノイドを扱うことができるようになる.

因みにモノイドとは,ある集合$M$と$M$上で定義された演算$*$と単位元$e$の組$(M,*,e)$で次を満たすもののことである.

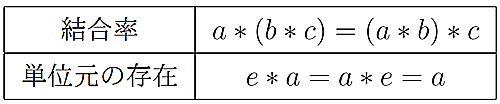Monoid

ここでは,自己準同系とその合成で構成されるEndoモノイドを紹介する

      import Data.Monoid a = Endo (3 +)
b = Endo (4 *)
c = mappend a b
    

プログラム上の(3 +)は,左から$3$を足す操作,(4 *)は左から$4$をかける操作を表していて,Endoは,(3 +)や,(4 *)

がEndoモノイドの元であることを宣言している.mappend関数は，モノイドの演算を適応する関数で,Endoモノイドの場合,準同系の合成を表している. 実際に実行してみると次のようになる.

      > appEndo a 1
4
> appEndo a 2
5
> appEndo b 1
4
> appEndo b 2
8
> appEndo c 2
11
    

appEndo関数はEndoモノイドの元に値を代入する関数である.

      import Data.Monoid f x = Endo (x +)
numL = [1 .. 10]
endoL = map f numL sEndo = mconcat endoL
    

mconcatはモノイドの元のリストを引数に取り,順にモノイドの演算を適用し,新たなモノイドの元を得る関数である.今回のEndoモノイドの場合,mconcatは自己準同系のリストから,それらを合成した新たな自己準同系を作り出す関数である.

実際に実行すると.

      > appEndo sEndo 0
55
    

他にも半群などの基本的な代数的構造を標準ライブラリでサポートしているのもこの言語の魅力と言える.Haskellと数学者は親和性が高いことが容易に察せられる.

Hask圏

HaskellはHaskellの型を対象とし,Haskellの関数を射とする圏を成している.

因みに圏$C$とは対象の類$\mathrm{ob}(C)$と対象の間の射の類$\mathrm{hom}(C)$からなり,次を満たす物のことである.

Cat

例えば以下の図式は今まで出てきたHaskellの型や関数を用いた可換図式である.sum関数はリストを引数に取り各要素を足し合わせる関数である.

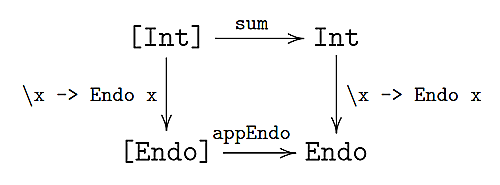zushiki

さらに,HaskellはFunctor型がサポートされていて,これはそのまま圏論で言う関手のことである.高級関数を用いて処理を一般化していたが,これはHask圏の部分圏の関手と見ることができる.つまりこのFunctorを用いることでさらに処理を一般化することも可能となる.しかし逆にプログラミング言語としてHaskellを用いるだけでなく,代数的構造のシミュレーターや,ちょっとしたおもちゃとして用いることにも向いていると思う.

まとめ

ここまでHaskellの特徴や便利な点や優れている点を述べてきた.しかし,Haskellは他の言語と違い学習コストが高い印象がある.さらに今まで述べてきた優れている点は，数学に触れている者目線での優れている点であるので,一般にはかなり難しい言語だと思う.実際に一般用途として用いられた例も,医療用電子カルテや金融機関でのシステム
,モナデウス(シューティングゲーム)など,数えるほどでしかない.しかし,Haskellを学ぶと“いい書き方”に矯正される.(Haskellが“いい書き方”を要求するから.)これは他の言語でのコーディングをより効果的にするもので,この点もHaskellを学ぶ意義の$1$つではないだろうか.

この他にもHaskellには優れた点が存在し,隠された魅力もまだまだ残されている.

プログラミング言語を学習するとき,Haskellも選択肢に$1$つ加えてみてはどうだろうか.