カラーレンマについて
Mathlogに初めて投稿します。よろしくお願いします。
自分の勉強のために書いているので、誤りを多く含む可能性が高いです。
導入
今回は、双曲幾何で有名な補題「カラーレンマ」についてまとめたいと思います。「カラー(collar)」とは日本語で「えり」のことです。つまり、「カラーレンマ」は「えり補題」ということですね。名前は可愛らしいですが、結構パワフルな補題なのです。
実は、この補題は、ニールセン-サーストン分類定理という曲面上の写像類を分類する定理の証明で大切な役割を果たします。また、カラーレンマにより、双曲閉曲面の形状がある程度、制限されていることも分かります。
それでは、まずは、カラーレンマのイメージについて述べることにしましょう。まず、「パンツ」の3つの穴に、穴の大きさに依る「えり」をつけます。イメージ的には、穴が小さければ、太いえりがついて、穴が大きければ、細いえりが付きます。カラーレンマは、「どんなパンツであっても、その襟たちが、互いにぶつかってしまうことはない。」ということを主張する命題です。
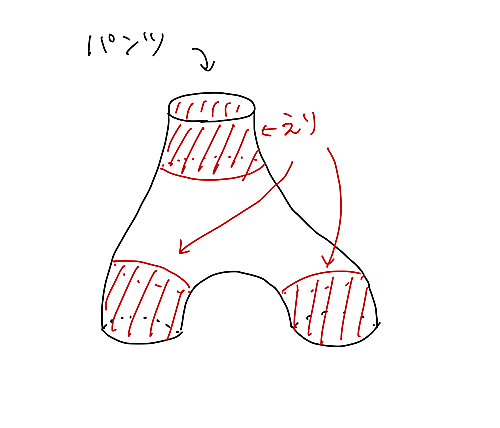カラーレンマのイメージ
主張と証明
カラーレンマの主張
それでは、カラーレンマの主張を見てみましょう。
$P$を双曲構造の入ったパンツ、$\gamma_1,\gamma_2,\gamma_3$を$P$の測地的境界線とする。このとき、各$\gamma_j\ (j=1,2,3)$のえり近傍
$$C(\gamma_j)=\{\ p \in P\ |\ \sinh \lambda(p,\gamma_j)\sinh L(\gamma_j) \leq 1\ \}$$
は互いに交わることはなく、それぞれはアニュラスに同相である。ただし、$\lambda$は双曲距離である。
用語の説明をします。「双曲構造の入ったパンツ」とは、下図のように、上半平面上の一つの辺を共有する等長的な二つの直角六角形$H,H'$を対応する辺同士で貼り合わせて得られる曲面です。こうして、作った曲面に現れる3つの境界が「測地的境界線」です。「アニュラス」とは基本群が$\mathbb{Z}$となるような曲面のことです。
（厳密に言うならば、位相的なパンツに双曲計量をいれて、境界が完備な測地線になっているもの(=双曲構造の入ったパンツ)は、すべてこの構成によって得られる、ということになると思います。）
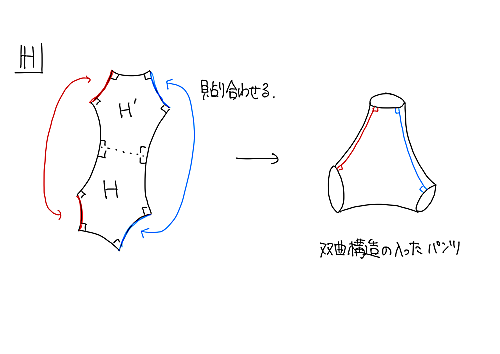双曲構造の入ったパンツ
(この図では、どちらかと言えば、ポアンカレ円板上の絵のように見えますが、あくまでイメージのつもりです。)
えり近傍$C(\gamma_j)$のイメージをしましょう。
$$ \sinh \lambda(p,\gamma_j) \sinh (L(\gamma_j)/2) \leq 1 \Leftrightarrow\lambda(p,\gamma_j) \leq \sinh^{-1}\left(\frac{1}{\sinh(L(\gamma_j)/2)}\right)
$$
ですから、$\gamma_j$からの距離が、$\sinh^{-1}\left(\frac{1}{\sinh(L(\gamma_j)/2)}\right)$以下となるような点がえり近傍$C(\gamma_j)$には含まれています。
カラーレンマの証明
貼り合わせる前の段階で考える。以下、辺の名前と長さを同じ記号で表すことがある。$C(\gamma_j)\cap H = N_j$とする。図のように対応する辺を与えると、$L(\gamma_j)=2c_j\ (j=1,2,3)$となる。ここで、直角六角形$H$を、$c_3$から向かい合う辺へ引いた最短測地線$\alpha$で切る。このとき、$c_1$側にできる直角五角形$F$の$c_1$と$\alpha$に挟まれた辺を$d$とし、$\alpha$によって分けられる$c_3$の$F$に属する線分を$x$としよう。このとき、直角五角形の辺の長さの関係式より、
$$\sinh c_1 \sinh d = \cosh x > 1$$
となる。したがって、
$$ d = \sinh ^{-1} \left( \frac{\cosh x}{\sinh c_1}\right) >\sinh ^{-1} \left( \frac1{\sinh c_1}\right) = \sinh ^{-1} \left( \frac1{\sinh ( L(\gamma_1)/2) }\right)$$
これは、$\gamma_2$に対しても同じことがいえるので、$N_1\cap N_2 = \emptyset$が示される。$H'$でも同様あるから、$C(\gamma_1)\cap C(\gamma_2)=\emptyset$となる。$\gamma_1$と$\gamma_3$、$\gamma_2$と$\gamma_3$に対しても同様であるから、補題が示された。
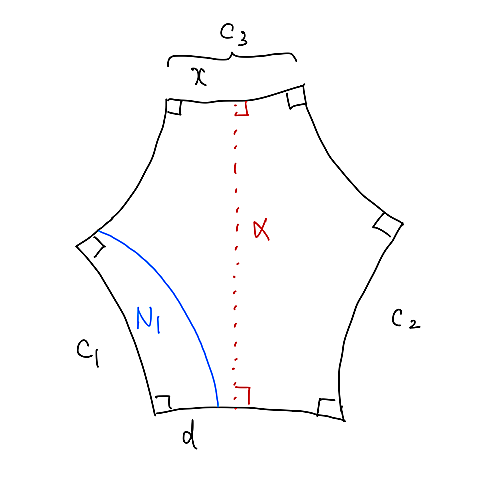カラーレンマの証明図
直角五角形の辺の長さの関係式とは、
図のような直角五角形に対して、次の関係式が成り立つ。
- $\tanh a \cosh b \tanh c = 1$
- $\sinh a \sinh b = \cosh d$
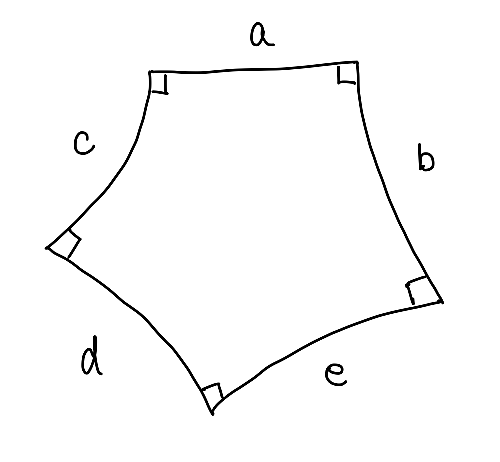直角五角形
のことです。証明は[谷口,奥村]などを参照してください。
命題1の証明の中で、少し注意しなければならない点があります。
- $\alpha$が$H$の中にあるのはどうしてでしょうか。
- $N_1$が$\alpha$を越えることは無いのでしょうか。
これについては、省略しておこうと思います。
応用
互いに交わる閉測地線の長さを制御する
ここからは、カラーレンマの応用を述べたいと思います。
$S$を連結な向き付けられた閉曲面で、種数$g$が$2$以上であるとします。$R$を$S$と同相な双曲計量の入った曲面(つまり、リーマン面)としましょう。$R$上の単純閉測地線$\gamma,\delta$が互いに交わるとき、これらの長さの関係はどのようになっているでしょうか。これについて、次の命題が成り立ちます。
リーマン面$R$上の単純閉測地線$\gamma,\delta\ (\gamma\neq \delta)$が互いに交わるとする。このとき、
$$\sinh(L(\gamma)/2)\sinh(L(\delta)/2) \geq 1$$
が成り立つ。
$y=2\sinh^{-1}\left(\frac1{\sinh(x/2)}\right)$のグラフが以下のような感じですから、$\gamma$と$\delta$が同時にものすごく小さくなることは無い、ということがわかります。
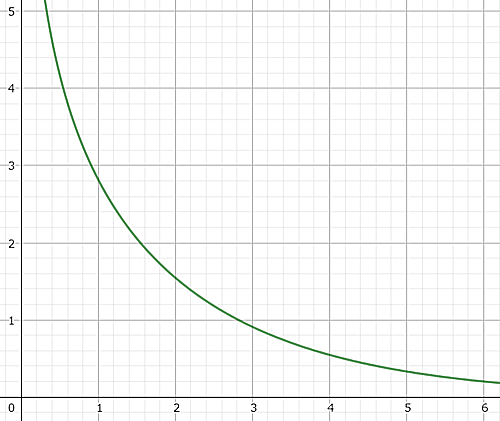hyp sin
では、証明に移っていきましょう。
まず、$\gamma$を含むような、$R$のパンツ分解を与える$3g-3$個の単純閉測地線の族$\{L_j\}$と$\{L_j\}$による$R$のパンツ分解$\{P_i\}$を考える。（$\gamma$と交わらない単純閉測地線の族で極大なものを与えれば、それがパンツ分解を与える。）$\gamma$を測地的境界線として持つ2つパンツ$P_l,P_m$に対して（$l=m$となる場合もある）、$P_l,P_m$上の$\gamma$のカラー近傍をそれぞれ$C_l(\gamma),C_m(\gamma)$とする。$\delta$は$\gamma$と交わることから、$\delta$はそれぞれのカラー近傍とも交わる。したがって、$\delta\cap(\partial C_l(\gamma) \setminus \gamma)$の元を$p_l$とし、$p_m$も同様に定める。このとき、カラーレンマから、
$$L(\delta) \geq \lambda(p_l,\gamma)+\lambda(p_m,\gamma)\geq 2 \sinh^{-1} \left(\frac1{\sinh(L(\gamma)/2)}\right)$$
となり、命題が成り立つ。
パンツ分解を与えるところの議論に行間がありますが、省略しておきます。
また、証明の最後でカラーレンマを用いています。カラー近傍が、アニュラスと同相なので、このような議論ができます。
参考文献
- [谷口,奥村] 谷口雅彦,奥村善英: 双曲幾何学への招待-複素数で視る-, 培風館
- [谷口,今吉] 谷口雅彦,今吉洋一: 新版タイヒミュラー空間論, 日本評論社
- [F,M] B.Farb, D.Margalit: A Primer on Mapping Class Groups, Princeton University Press
