ディガンマ関数の基本性質と積分表示

3340

こんにちは，たい焼きです．最近は問題の解説記事ばかり書いていたので，1つのテーマに絞って記事を書くのが久々な気がします．（というかこれが2つ目）今回はディガンマ関数の積分表示の導出に焦点を当てていきたいと思います

ディガンマ関数の定義・基本性質

ディガンマ関数は，ガンマ関数の対数微分で定義されます．

・ディガンマ関数の定義
ガンマ関数

Γ (z)

対し，

ψ (z) = \frac{d}{d z} \ln Γ (z) = \frac{Γ^{'} (z)}{Γ (z)}

基本性質についてですが，神鳥奈紗さんのPDFに証明とセットで書かれているので省略します．以下を参照してください．（おい）
https://twitter.com/sounansya_29/status/1320736570027110400?s=21
........................さすがに雑すぎる気がしたのでとりあえず列挙しておきます．

・漸化式

ψ (z + 1) = ψ (z) + \frac{1}{z}

・相反公式

ψ (1 - z) - ψ (z) = π \cot π z

・特殊値

ψ (1) = - γ

，

ψ (\frac{1}{2}) = - γ - 2 \ln 2

上の2つはガンマ関数の性質で対数微分を用いることで容易に導出でき， $ψ (1)$ はガンマ関数の無限乗積表示を用いることで以下のように導出できます．
$\begin{array}{rcl} ψ (z) & = & \frac{d}{d z} \ln Γ (z) \\ = & \frac{d}{d z} \ln lim_{n \to \infty} \frac{n^{z} n!}{\prod_{k = 0}^{n} (z + k)} \\ = & \frac{d}{d z} lim_{n \to \infty} (z \ln n + \ln n! - \sum_{k = 0}^{n} \ln (z + k)) \\ = & lim_{n \to \infty} (\ln n - \sum_{k = 0}^{n} \frac{1}{z + k}) \end{array}$
$z = 1$ として，
$ψ (1) = lim_{n \to \infty} (\ln n - \sum_{k = 1}^{n} \frac{1}{k}) = - γ$
を得ます． $ψ (\frac{1}{2})$ の方は，後ほど示す積分表示から得られます．
　結局導出を書きました．自分偉い！！！！！
　また，ディガンマ関数の積分表示の導出にポリガンマ関数（ディガンマ関数の高階微分）も用いるので，そちらについても軽く載せておきます．

・ポリガンマ関数の定義
ディガンマ関数

ψ (z)

対し，

ψ^{(m)} (z) = \frac{d^{m}}{{d z}^{m}} ψ (z)

ポリガンマ関数にも漸化式や相反公式は存在しますが，簡単に導けるので省略します．

ディガンマ関数の積分表示

この記事の本題ですね．wikipediaのディガンマ関数の解説ページに掲載されている積分表示の上から3つを全て証明していきます．
https://ja.wikipedia.org/wiki/%E3%83%87%E3%82%A3%E3%82%AC%E3%83%B3%E3%83%9E%E9%96%A2%E6%95%B0
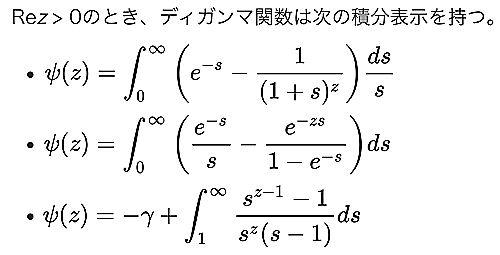Wikipediaより　
　ただし，これらを導く上でディガンマ関数の差の積分表示とオイラーの定数 $γ$ の積分表示を用います．

・ディガンマ関数の差の積分表示

ψ (y) - ψ (x) = \int_{0}^{1} \frac{t^{x - 1} - t^{y - 1}}{1 - t} d t

$\begin{array}{rcl} \int_{0}^{1} \frac{t^{x - 1} - t^{y - 1}}{1 - t} d t & = & lim_{a \to 0} (\int_{0}^{1} t^{x - 1} (1 - t)^{a - 1} d t - \int_{0}^{1} t^{y - 1} (1 - t)^{a - 1} d t) \\ = & lim_{a \to 0} (B (x, a) - B (y, a)) \\ = & lim_{a \to 0} (\frac{Γ (x) Γ (a)}{Γ (x + a)} - \frac{Γ (y) Γ (a)}{Γ (y + a)}) \\ = & lim_{a \to 0} \frac{\frac{Γ (x)}{Γ (x + a)} - \frac{Γ (y)}{Γ (y + a)}}{\frac{1}{Γ (a)}} \\ = & lim_{a \to 0} \frac{\frac{Γ (y) ψ (y + a)}{Γ (y + a)} - \frac{Γ (x) ψ (x + a)}{Γ (x + a)}}{- \frac{ψ (a)}{Γ (a)}} \\ = & - lim_{a \to 0} (\frac{Γ (y) ψ (y + a)}{Γ (y + a)} - \frac{Γ (x) ψ (x + a)}{Γ (x + a)}) \frac{Γ (a + 1)}{a ψ (a + 1) - 1} \\ = & ψ (y) - ψ (x) ◻ \end{array}$

（神鳥奈紗さんのPDFから引用）
　これを用いて，ポリガンマ関数の積分表示を導出します．

・ポリガンマ関数の積分表示

ψ^{(m)} (z) = (- 1)^{m + 1} \int_{0}^{\infty} \frac{s^{m} e^{- z s}}{1 - e^{- s}} d s (m > 0)

ディガンマ関数の差の積分表示において $x = 1$ ， $y = z$ とすると，
$\begin{array}{rcl} ψ (z) & = & ψ (1) + \int_{0}^{1} \frac{1 - t^{z - 1}}{1 - t} d t \\ = & ψ (1) + \int_{0}^{\infty} \frac{e^{- s} - e^{- z s}}{1 - e^{- s}} d s 〈 t = e^{- s} 〉 \end{array}$
これの両辺を $m$ 回微分することで，積分表示が得られる． $◻$

　導出する1つ目の積分表示は以下の式です．（都合上，wikipediaに並んでいる順番とは異なります）

・ディガンマ関数の積分表示➀

ψ (z) = - γ + \int_{1}^{\infty} \frac{s^{z - 1} - 1}{s^{z} (s - 1)} d s

$\begin{array}{rcl} \int_{1}^{\infty} \frac{s^{z - 1} - 1}{s^{z} (s - 1)} d s & = & \int_{1}^{\infty} \frac{1}{s^{z} (s - 1)} \int_{0}^{z - 1} \frac{d}{d t} s^{t} d t d s \\ = & \int_{1}^{\infty} \frac{\ln s}{s^{z} (s - 1)} \int_{0}^{z - 1} s^{t} d t d s \\ = & \int_{0}^{z - 1} \int_{1}^{\infty} \frac{s^{t - z} \ln s}{s - 1} d s d t \\ = & \int_{0}^{z - 1} \int_{0}^{\infty} \frac{x e^{x (t - z)}}{e^{x} - 1} e^{x} d x d t 〈 x = \ln s 〉 \\ = & \int_{0}^{z - 1} \int_{0}^{\infty} \frac{x e^{x (t - z)}}{1 - e^{- x}} d x d t \\ = & \int_{0}^{z - 1} ψ^{(1)} (z - t) d t \\ = & {[- ψ (z - t)]}_{0}^{z - 1} \\ = & - ψ (1) + ψ (z) \end{array}$

$ψ (1) = - γ$ より， $ψ (z) = - γ + \int_{1}^{\infty} \frac{s^{z - 1} - 1}{s^{z} (s - 1)} d s$ が示された． $◻$

5行目から6行目の変形で，ポリガンマ関数の積分表示を用いたことに注意してください．
　2つ目の証明に移る前に，オイラーの定数の積分表示を確認しておきましょう．

・オイラーの定数

γ

の積分表示

γ = \int_{0}^{\infty} (\frac{1}{e^{t} - 1} - \frac{e^{- t}}{t}) d t

これの証明は，以下のページを参照してください．
https://ja.wikipedia.org/wiki/%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E3%81%AE%E5%AE%9A%E6%95%B0
　では，2つ目の積分表示の導出をしていきましょう．

・ディガンマ関数の積分表示➁

ψ (z) = \int_{0}^{\infty} (\frac{e^{- t}}{t} - \frac{e^{- z t}}{1 - e^{- t}}) d t

$\begin{array}{rcl} \int_{0}^{\infty} (\frac{e^{- t}}{t} - \frac{e^{- z t}}{1 - e^{- t}}) d t & = & \int_{0}^{\infty} (\frac{e^{- t}}{t} - \frac{1}{e^{t} - 1}) d t + \int_{0}^{\infty} (\frac{1}{e^{t} - 1} - \frac{e^{- z t}}{1 - e^{- t}}) d t \\ = & - γ + \int_{0}^{\infty} \frac{e^{- t} - e^{- z t}}{1 - e^{- t}} d t \end{array}$

これは，ポリガンマ関数の積分表示の導出で出てきた形に他ならない．したがって， $ψ (z) = \int_{0}^{\infty} (\frac{e^{- t}}{t} - \frac{e^{- z t}}{1 - e^{- t}}) d t$ が示された． $◻$

積分の形がオイラーの定数の積分表示に似ていることから変形していくと上手く示せましたね．1つ目のよりはかなり易しかったと思います．
　では，3つ目の積分表示の導出をしていきましょう．

・ディガンマ関数の積分表示➂

ψ (z) = \int_{0}^{\infty} (e^{- t} - \frac{1}{(1 + t)^{z}}) \frac{d t}{t}

先ほど導出したディガンマ関数の積分表示➁を変形して，これを示す．
$\begin{array}{rcl} ψ (z) & = & \int_{0}^{\infty} (\frac{e^{- t}}{t} - \frac{e^{- z t}}{1 - e^{- t}}) d t \\ = & lim_{δ \to + 0} (\int_{δ}^{\infty} \frac{e^{- t}}{t} d t - \int_{δ}^{\infty} \frac{e^{- z t}}{1 - e^{- t}} d t) \\ = & lim_{δ \to + 0} (\int_{δ}^{\infty} \frac{e^{- t}}{t} d t - \int_{e^{δ} - 1}^{\infty} \frac{(1 + s)^{- z}}{1 - (1 + s)^{- 1}} \frac{d s}{1 + s}) 〈 s = e^{t} - 1 〉 \\ = & lim_{δ \to + 0} (\int_{δ}^{\infty} \frac{e^{- t}}{t} d t - \int_{e^{δ} - 1}^{\infty} \frac{1}{t (1 + t)^{z}} d t) \end{array}$
区間 $[δ, e^{δ} - 1]$ で $\frac{1}{t (1 + t)^{z}}$ を評価すると， $R e (z) > 0$ より
$0 \leq \frac{1}{t (1 + t)^{z}} \leq \frac{1}{t} \leq \frac{1}{δ}$
したがって，定積分を以下のように評価できる．
$| \int_{δ}^{e^{δ} - 1} \frac{1}{t (1 + t)^{z}} d t | \leq | \int_{δ}^{e^{δ} - 1} \frac{1}{δ} d t | \leq O (δ)$
これより，
$\begin{array}{rcl} ψ (z) & = & lim_{δ \to + 0} (\int_{δ}^{\infty} \frac{e^{- t}}{t} d t - \int_{δ}^{\infty} \frac{1}{t (1 + t)^{z}} d t) \\ = & lim_{δ \to + 0} \int_{δ}^{\infty} (e^{- t} - \frac{1}{(1 + t)^{z}}) \frac{d t}{t} \\ = & \int_{0}^{\infty} (e^{- t} - \frac{1}{(1 + t)^{z}}) \frac{d t}{t} \end{array}$
となるので，示された． $◻$

導出する式の形が2つ目の積分表示に似ていたので方針は立てやすかったと思いますが，発散する積分を項別に分けて計算することはできない（修正前は分けた状態で投稿してました...）ので，極限を考える必要があります．変数変換によって生まれてしまう積分区間の誤差は $δ$ の1次と同位の微少量なので，極限 $δ \to + 0$ を取ると0に収束しますね．