最小二乗法とその幾何学的解釈
はじめに
なにかと説明する場面が多い最小二乗法ですが、ここでは最小二乗法(Least Squares Method,$LSM$)の基礎と幾何学的解釈について解説します。この記事では話を簡単にするために、一般線形モデル($GLM$)$\ Y=Xβ+ε\ $における単回帰モデル$y_i=β_0+β_1x_i$を想定した話で展開していきます。なお誤差$ε$に関しては、不偏性と等分散性が成り立っているものとします。
正規方程式
$LSM$は、以下の残差二乗和(Residual Sum of Squares,$RSS$)を最小にするようなパラメータ$\hat β$を推定する方法でした。
$RSS=(Y-X\hat β)'(Y-X\hat β)$
これを最小たらしめる$\hat β$は、一階条件によって$\frac{∂RSS}{∂β}=0$で求められます。実際にこれは、$\frac{∂RSS}{∂β}=-2X'Y+2X'X\hat β=0\ $という正規方程式の形になり、これを解けば$\ \hat β=(X'X)^{-1}X'Y\ $が求まります。
最小二乗法のおもな性質
$\hat β$の期待値に関しては、$E(\hat β)=β$が成り立つ。つまり$\hat β$は$β$の不偏推定量である。
$E[(X'X)^{-1}X'Y]=(X'X)^{-1}X'E(Y)=β$
$\hat β$の分散に関しては、$V(\hat β)=σ^2(X'X)^{-1}$が成り立つ。
$V[(X'X)^{-1}X'Y]=(X'X)^{-1}X'V(Y)[(X'X)^{-1}X']'=σ^2(X'X)^{-1}X'X(X'X)^{-1}=σ^2(X'X)^{-1}$
ある特定の条件を満たしていると$\hat β$は$BLUE$である。
$LSM$の幾何学的解釈
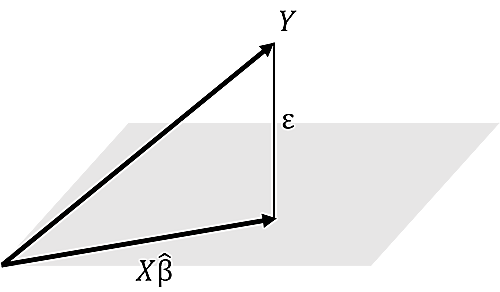実は三平方の定理の関係だったりする
シンプルな図を載せましたが、結論から言えば、最小二乗法は三平方の定理で解釈できます。
$X$が張る部分空間へ$Y$を射影するような正射影行列$P_X$を用意すると、$P_X=X(X'X)^{-1}X'$であるため、$X\hat β$は$P_XY$と表せます。一方で残差$ε=Y-X\hat β$は$(1-P_X)Y$と表せます。$P_X$は正射影行列なので、$ε$と$X\hat β$が直交していることと同義であることに注意してください。
参考文献
- 佐和隆光 「回帰分析」,朝倉書店,1979
- Stephen Boyd & Lieven Vandenberghe,"Introduction to Applied Linear Algebra",Cambridge University Press,2018
この記事を高評価した人
この記事に送られたバッジ
投稿者
