原子核に潜むSU(4)~アイソスピンと原子核入門~
皆さんこんにちは,Y・Yです。この記事はWathematica Advent Calender2024の12月14日の分として書きました。後輩たちが力作をたくさん書いていて凄いなぁと思います。素粒子でも物性でもない謎の分野,原子核について紹介します。
そもそも,原子核とは
 原子と原子核
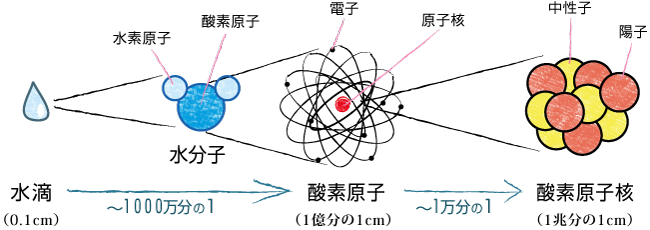
原子と原子核
私たちの身の回りにある物質は,原子という非常に小さな粒子からできている,とまず私たちは中学校の化学で習います。さらに中3だか高校1年になると原子というのは中心にある原子核とその周りを"軌道運動"する電子から出来ていて,原子核はさらに陽子と中性子からできていることを学びます。(画像は理化学研究所仁科加速器科学研究センターから)化学や物性物理では,この電子が主役となって物質の非常に様々な構造を解き明かすわけです。しかし,よく考えてみると原子核というのも陽子と中性子からなる量子多体系であり,非常に豊かな構造を持つわけです。その中でも特に大事な「アイソスピン」という概念について少し紹介してみたいと思います。
陽子と中性子は同じ粒子?
第1章で原子核は陽子と中性子という2種類の粒子からできているということを述べました。しかし,陽子と中性子の質量は非常に似通った値を取る(わずかに中性子の方が重い)ということは高校で習ったと思います。
| 粒子 | 質量 (MeV/c²) |
|---|---|
| 陽子 | 938.27 |
| 中性子 | 939.56 |
そこで,これら二つは異なる粒子ではなく,そもそも同じ粒子の異なる状態であるという考えに至ります。つまり,2準位系
\begin{equation}
\ket{p}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ket{n}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}
\end{equation}
を考えるわけです。
2準位系ですので,これらはユニタリ変換$SU(2)$で移りあいます。これはスピンと全く同じ変換性を有するので,生成子はパウリ行列
\begin{equation}
\tau_1 =
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix},
\quad
\tau_2 =
\begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix},
\quad
\tau_3 =
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}.
\end{equation}
で表せます。(スピンと異なる空間の生成子であることを強調するために,$\tau$で表しています。)ここで
\begin{equation}
\mathbf{T}=\frac{1}{2}\mathbf{\tau}
\end{equation}
を導入します。これをアイソスピン(荷電スピン)演算子と呼び,スピン演算子$\mathbf{S}$と全く同じ代数構造を持ちます。この意味で陽子はアイソスピン$T_3=\frac{1}{2}$を,中性子はアイソスピン$T_3=-\frac{1}{2}$の状態です。この二つを合わせて核子と呼び,アイソスピン$T=\frac{1}{2}$が割り当てられます。また,アイソスピン演算子の作用する空間を荷電空間と呼びます。
アイソスピンの$T_1$や$T_2$は物理的な意味を持ちません。さらに,重ね合わせ状態
\begin{equation}
\frac{\ket{p}+\ket{n}}{\sqrt{2}}
\end{equation}
等の状態にある粒子は自然界には存在しません。(超選択則)それならばアイソスピンを考えることに意味はあるのでしょうか。
実は,アイソスピンは複合粒子を考える際に非常に有用な指針となります。それは,核力にはアイソスピンの第3成分を特別視しないからです。これを核力の荷電独立性と言います。最も簡単な例として,重陽子を見ていきましょう。重陽子は陽子と中性子が結合した状態です。これは
\begin{equation}
T_3\ket{D}=0
\end{equation}
と書かれますが,核力はアイソスピンの第三成分を区別しないので,
\begin{equation}
T^2\ket{D}=0
\end{equation}
でなくてはなりません。これは,重陽子がアイソスピン一重項
\begin{equation}
\ket{D}=\frac{1}{\sqrt{2}}(\ket{p}\ket{n}-\ket{n}\ket{p})
\end{equation}
であることを表します。これは,核子がFermionであることを考慮すると,波動関数に強い制限を与えます。位置規定の波動関数を$\psi(\mathbf{r}_1,\mathbf{r}_2)$,スピン波動関数を$\xi(1,2)$アイソスピン波動関数を$\chi(1,2)$とすると,粒子の交換に対し波動関数は反交換であるから,
\begin{equation}
\psi(\mathbf{r}_1,\mathbf{r}_2)\xi(1,2)\chi(1,2)=-\psi(\mathbf{r}_2,\mathbf{r}_1)\xi(2,1)\chi(2,1)
\end{equation}
となります。アイソスピン1重項のアイソスピン波動関数は反対称なので,重陽子に対しては
\begin{equation}
\psi(\mathbf{r}_1,\mathbf{r}_2)\xi(1,2)\chi(1,2)=\psi(\mathbf{r}_2,\mathbf{r}_1)\xi(2,1)
\end{equation}
でなくてはならないという強い条件を与えます。実際に,重陽子はスピン1を持ち,軌道角運動量は偶数しか取りません。
素粒子の言葉でアイソスピンを見ると
陽子や中性子はハドロンと呼ばれるクォーク複数からなる複合粒子の一種であることが分かっています。例えば陽子は$(u,u,d)$,中性子は$(u,d,d)$という三つのクォークからできています。クォークの質量を表にしてみると,アップクォークとダウンクォークだけ非常に質量が軽く,ほとんど同じ質量とみなせることが分かります。
| クォーク | 質量 (MeV/c²) | 備考 |
|---|---|---|
| アップ (u) | 2.16 | アイソスピン$T_3=\frac{1}{2}$ |
| ダウン (d) | 4.67 | アイソスピン$T_3=-\frac{1}{2}$ |
| ストレンジ (s) | 93.5 | |
| チャーム (c) | $ 1.27\times 10^3$ | |
| ボトム (b) | $4.18\times 10^3 $ | |
| トップ (t) | $1.72\times 10^5$ |
さらに,素粒子の標準模型における強い力を記述するラグランジアン密度
\begin{equation}
\mathcal{L}_{\text{QCD}} = -\frac{1}{4} F^{a}_{\mu\nu} F^{a\mu\nu}
+ \sum_{f} \bar{\psi}_{f} \left( i \gamma^{\mu} D_{\mu} - m_f \right) \psi_{f}
\end{equation}
では,クォークのフレーバーは質量$m_f$でしか寄与しません。そのため,強い力を考える限りにおいてはアップクォークとダウンクォークは1つの素粒子の異なる状態だとみることが出来ます。($SU(2)$フレーバー対称性)そこで,陽子や中性子のアイソスピンと整合性を合わせるためにアイソスピン$T_3=\frac{1}{2}$ をアップクォークに,アイソスピン$T_3=-\frac{1}{2}$ を割り当てます。実際に格子QCDを用いた数値計算においても$SU(2)$フレーバー対称性を持たせた計算(2+1フレーバーQCD)をすることで,目覚ましい結果を上げることに成功しています。
脱線 弱アイソスピンについて
 素粒子の標準模型(higgstan.com より)
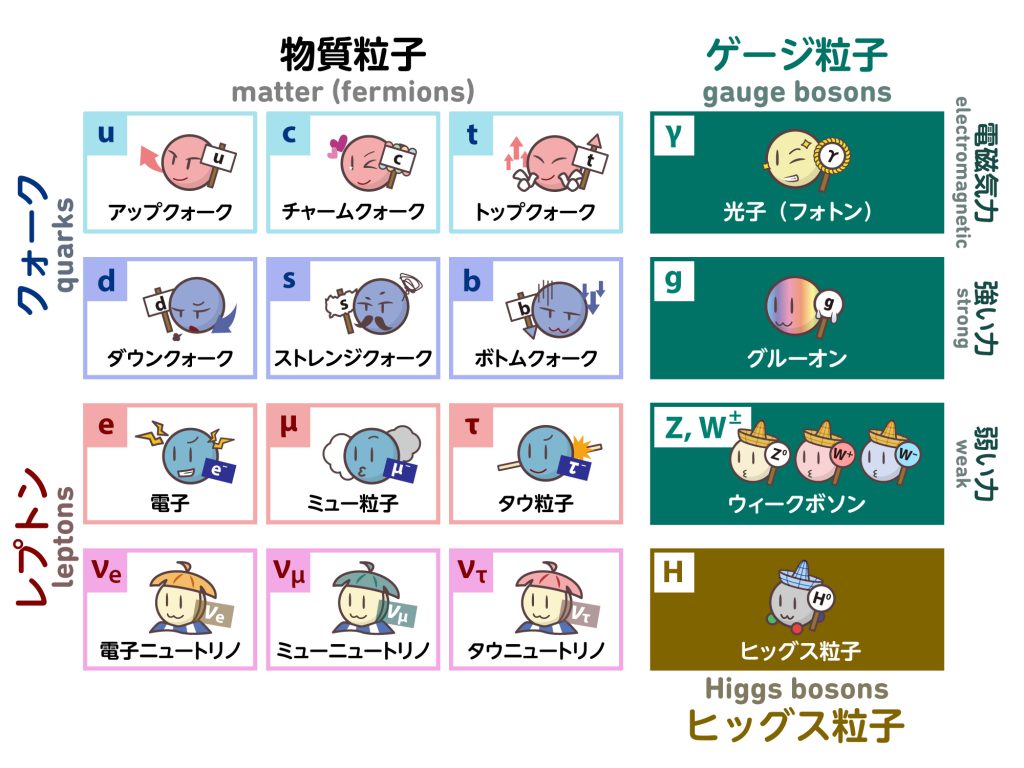
素粒子の標準模型(higgstan.com より)
素粒子の弱い相互作用を記述するWinberg-Salam 理論では質量0の左巻きレプトン同士は2重項をなし
$$ \begin{pmatrix} \nu_e \\ e \end{pmatrix}_L, \begin{pmatrix} \nu_\mu \\ \mu\end{pmatrix}_L, \begin{pmatrix} \nu_\tau \\ \tau \end{pmatrix}_L$$
というペアを作り,それらにたいして$SU(2)$が作用します。この2重項の各成分をアイソスピンとの類推で弱アイソスピンと呼び,人によってはアイソスピンと呼ぶことがあります。確かに中性子($d$クォーク)は陽子($u$クォーク)にβ崩壊する(また逆も然り)訳ですので,一見これは問題無さそうです。しかし,実際の弱い相互作用に対してはクォークのフレーバー(質量固有状態)と$SU(2)_W$の固有状態は一致せず小林-益川(CKM)行列で混合します。したがって,これはフレーバー$SU(2)$対称性であるアイソスピンとは区別した方がよい場合があります。ただし,ストレンジクォークの質量は重い上,CKM行列の非対角項の効果は小さいため,低エネルギー領域では弱い相互作用はアイソスピンに作用すると有効的に考えてもよいです。しかし,中性子性内部では核子からハイペロン(ストレンジクォークを含んだバリオン)への$\beta$崩壊の効果が無視できず,ハイペロンを含んだ原子核の研究は現在の原子核研究の最先端の問題の一つです。
核力の$SU(4)$対称性
QCDのラグランジアン密度は相当すっきりした形で書けるわけですが,それを用いて核力ポテンシャルを導くというのは非常に難解な問題になります。
核力ポテンシャルはスピンやアイソスピンに強く依存します。具体的には核力ポテンシャルの項の中にはHeisenberg項
$$\frac{1}{2} \left( 1 + \mathbf{\sigma}_1 \cdot \mathbf{\sigma}_2 \right)V_H(r)$$
やMajorana項
$$\frac{1}{2} \left( 1 + \mathbf{\sigma}_1 \cdot \mathbf{\sigma}_2 \right)\left( 1 + \mathbf{\tau}_1 \cdot \mathbf{\tau}_2 \right)V_M(r)$$
さらにテンソル力という非常に複雑な項が混ざります。
しかし,Wignerは近似的に核力ポテンシャルが核子の位置だけに依存するとした場合にどのようなことが言えるのかを考えました。
スピン対称性$SU(2)_{spin}$とアイソスピン対称性$SU(2)_{isospin}$はスピン空間とアイソスピン空間という異なる空間に作用する群なので,普通は
$$ SU(2)_{spin}\times SU(2)_{isospin} $$
という直積群を考えます。しかし,核力がスピンにもアイソスピンにも作用しないのならばこれはもっと大きな群
$$ SU(4)\geq SU(2)_{spin}\times SU(2)_{isospin}$$
の部分群として考えることが出来ます。これをWignerの$SU(4)$対称性といい,その微小変換は
$$ \delta N=i\varepsilon_{\mu\nu}\sigma^{\mu}\tau^{\nu}N \qquad N=\begin{pmatrix} p \\ n \end{pmatrix}$$
で表されます。ただし$\sigma^{0}=\tau^0=\hat{I} $で,ギリシャ添え字は0から3を動き,$\varepsilon_{\mu\nu}$は微小パラメタです。原子核にはこの$SU(4)$は
$$ SU(4)\otimes SU(4)\otimes\cdots SU(4)$$
というテンソル積表現として,スピン・アイソスピン空間のケット$\ket{s_1,t_1\cdots}$に作用します。
これはスピンもアイソスピンも変えてしまうようなめちゃくちゃな変換なわけですが,質量数(バリオン数)$A$,軌道角運動量$L$およびパリティ$\pi$を保存します。Wignerの仮定の上では軌道波動関数$\psi(\mathbf{r})$が同じで$SU(4)$の(テンソル積表現の)同じ規約表現に属する原子核は全く同じエネルギーを持ちます。これを超多重項と言います。
Wignerの$SU(4)$対称性はQCDの有効ラグランジアンから(近似的に)導くという研究成果もあり,単なる模型と断じきれない部分があります。
Gamow-Teller 遷移
Wignerの$SU(4)$の考え方が極めて有効に使える例の一つが$\beta$崩壊におけるGamow-Teller遷移です。これは原子核のスピンとアイソスピンを同時に変えるプロセスで,例えば
$$\ce{^6He\to^6Li} $$
がある。$\ce{^6He}$の基底状態0+は$L=0,S=0,T=1,Tz=-1$で,$\ce{^6Li}$の基底状態1+は$L=0,S=1,T=0,Tz=0$だと考えると,このプロセスは$SU(4)$超多重項の中での遷移となる。この遷移確率を超多重項を考慮して計算すると,この崩壊プロセスが高い確率で起きているという実験結果をよく説明します。
まとめ
原子核物理の「アイソスピン対称性」というかなり絞った(つもり)のトピックについて書いてみました。本文で紹介した以外にも,原子核の$SU(4)$対称性が$\alpha$粒子で満たされた物質中では破れるという論文が今年発表されていたり,重い原子核では$SU(4)$対称性が復活したりと思った以上に奥が深そうな話題で,結局ふかいところまでは理解しきれなかった部分があり,リベンジしたいです。素粒子スケールで見たり核子スケールで見たり,はたまた原子核全体のスケールで見たりと原子核のさまざまな切り口を知って貰って興味を持ってもらえたらと思います。
はたしてMathlogで書いたうまみはあったのか……
参考文献
[1]野上茂吉郎,基礎物理学選書 原子核,(1973)裳華房
原子核の話題が一通り載っていていい本です。アイソスピン対称性については少ししか書いてない。
[2]八木浩輔,朝倉現代物理学講座 原子核と放射 基礎的な問題への量子力学の応用(1980)朝倉書店
絶版。アイソスピンの符号がこの記事と逆なので注意。
[3]永江知文,ハドロン物理学入門(2020)裳華房
[4]青木慎也,格子QCDによるハドロン物理 クォークからの理解(2017)共立出版
[5]久後汰一郎,ゲージ場の量子論I,II(1989)培風館
この辺りは素粒子の箇所を書くためにちまちま参考にしました。
[6]山田勝美・森田正人・藤井昭彦,β崩壊と強い相互作用(1974)培風館
弱い相互作用に関係する現象論が全部載ってるけどWinberg-Salamは載ってないという今手に入る本の真逆を行く本。
[7]E. Wigner, On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei(1937)Phys.Rev.51,106
[8]E. Wigner, On the Structure of Nuclei Beyond Oxygen,(1937)Phys. Rev.51,947
Wignerの原論文。実は$SU(4)$とは書いてないが,$SU(4)$の規約分解をしてる。何をやってるのかわかりづらくてちゃんと読めてない。
[9]T. Mehen, I. W. Stewart, and M. B. Wise, Wigner Symmetry in the Limit of Large Scattering Lengths(1999)Phys. Rev. Lett. 83, 931
QCDからWignerの$SU(4)$を近似的に出している。
[10]Hiroyuki Tajima, Hajime Moriya, Tomoya Naito, Wataru Horiuchi, Eiji Nakano, Kei Iida,Polaronic neutron in dilute alpha matter: A p-wave Bose polaron(2024)doi:10.48550/arXiv.2408.15043
$\alpha$粒子マターでは核力の性質がかなり変わるかもという論文。これを読みたくて調べ始めたらドツボにハマった感がある。
[11]
仁科加速器科学研究センター
[12]
ひっぐすたん
イラストはこちらから頂いた。ひっぐすたんさんのやつは本当にありがたい。
[13]
Particle Data Group
一応核子の質量はここのものを適当に打ち切って使ってます。
