Edwardsによるヘロンの公式の複素数を使った証明
ヘロンの公式
$ \triangle ABC$の3辺の長さを$a,b,c$, 面積を$S$とするとき,
$S=\sqrt{s(s-a)(s-b)(s-c)}.$ ただし, $\displaystyle s=\frac{a+b+c}{2}.$
証明は余弦定理を用いたものがよく知られている. この記事では, Edwardsによる複素数の性質を使った見事な証明を紹介する.
Edwardsによる複素数を使った証明
以下の証明は, Edwardsの論文([1])をベースにして, 少し読みやすく書き直したものである. 以下, $\mathrm{i} $は虚数単位とする.
$\triangle ABC$の3辺の長さを$AB=c,BC=a,CA=b$, 内接円の半径を$r$とすると$S=\frac{1}{2}r(a+b+c)=rs.$
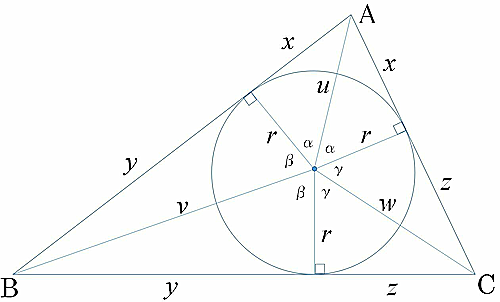
ここで, 図のように角度$\alpha,\beta,\gamma $, 長さ$x,y,z,u,v,w$を設定する. このとき, $\alpha+\beta+\gamma=\pi.$
また, $ \ x+y+z=s,\ x+y=c,\ y+z=a,\ z+x=b$より, $x=s-a,\ y=s-b,\ z=s-c.$
さらに, $(r+ \mathrm{i}x)(r+ \mathrm{i}y)(r+\mathrm{i}z)=ue^{\mathrm{i}\alpha}\cdot ve^{\mathrm{i}\beta}\cdot we^{\mathrm{i}\gamma}=uvwe^{\mathrm{i}(\alpha+\beta+\gamma)}=uvwe^{\mathrm{i}\pi}=-uvw. $
この式の虚部を比較して, $r^2(x+y+z)-xyz=0$. よって, $xyz=r^2(x+y+z)=r^2s.$
したがって, $\displaystyle 1=\frac{xyz}{r^2s}=\frac{sxyz}{(rs)^2}=\frac{s(s-a)(s-b)(s-c)}{S^2}$より $ \displaystyle S=\sqrt{s(s-a)(s-b)(s-c)}.$
(参考文献)
[1] M. D. Edwards, "A proof of Heron’s formula", The American Mathematical Monthly 114.10(2007)
