みゆ🌹の魔法 その１ 三角形の辺の比

みんな大好き（？）ピタゴラス数

　ピタゴラス数といえば、直角三角形の３辺の長さが整数となるような３つの整数の組のことですね。長さの比率が整数比つまり有理数比な直角三角形はピタゴラス三角形などと呼ばれるのですが、これを直角三角形以外の三角形にも拡張してみましょう。

　実は、 三辺の比を有理数比ではなく『有理数に無理数 $x$ を加えた拡大体 $\mathbb{Q}[x]$ の元の比』というように拡張してあげると、様々な内角をもつ三角形の三辺比を表すことができるんです。

魔法の手順

１．無理数 $x$ を用意します。

　例）$x=\varphi$（黄金数 $\varphi =\frac{1+\sqrt{5}}{2}$）

２．$x$ を有理数倍して $1$ より小さい数 $c$ を作り、三辺の比が $c:\sqrt{1-c^2}:1$ の直角三角形をかきます。

　例）$c=\frac{1}{2}x=\frac{\varphi }{2}$、$\frac{\varphi }{2}:\sqrt{1-\frac{{\varphi }^2}{4}}:1$
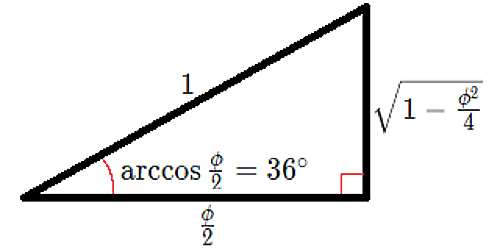手順２

３．任意の２整数 $a$ と $b$ $(a>b)$ を用意し、先程の直角三角形を $2b(a+bc)$ 倍します。

　$\to 2bc(a+bc):2b(a+bc)\sqrt{1-c^2}:2b(a+bc)$

　例）$a=2$、$b=1$、$2b(a+bc)=4+\varphi$倍
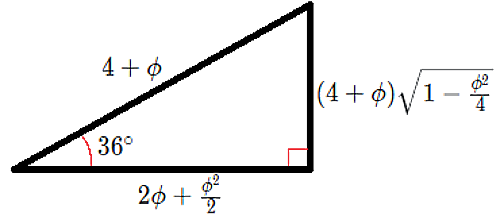手順３

４．$2bc(a+bc)$ 側の辺を鋭角側に $a^2-b^2$ だけ延長すると、そこからもう一方の鋭角側の頂点と結んでできる内側の三角形の三辺比は $\mathbb{Q}[x]$ の元で構成された比となっています。

　$\to a^2-b^2:2b(a+bc):a^2+b^2+2abc$

　例）$a^2-b^2:2b(a+bc):a^2+b^2+2abc=3:(4+\varphi ):(5+2\varphi )$
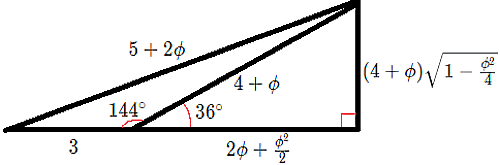手順４

ちなみに、$c$ は $x$ の有理数倍なので、$\mathbb{Q}[x]$ の元の一つですね。
もちろん $x$ は無理数じゃなくてもおっけーで、有理数の場合でも同じことができちゃいます。
$\pm \frac{1}{2}$ とかで試すとまた面白いかも♪♪

検証

　先程の例では、二辺の長さが $3$ と $(4+\varphi )$、その狭角が ${144}^{\circ }$、対辺の長さが $(5+2\varphi )$ という三角形ができました。
余弦定理を使って検証してみましょう。

$$\begin{gathered} 3^2+(4+\varphi {)}^2-2\cdot 3\cdot (4+\varphi )\cos {144}^{\circ } \\ =9+(16+{\varphi }^2+8\varphi )-(24+6\varphi )(-\frac{\varphi }{2}) \\ =25+{\varphi }^2+8\varphi +12\varphi +3{\varphi }^2 \\ =25+4{\varphi }^2+20\varphi \\ =(5+2\varphi {)}^2\leftarrow 合ってる!! \end{gathered}$$

$\theta =\pi -\arccos c$ とすれば $c=-\cos \theta$ ですので、一般には次のように表せるはずです。

$$(a^2-b^2{)}^2+(2b(a-b\cos \theta ){)}^2-2(a^2-b^2)(2b(a-b\cos \theta ))\cos \theta =(a^2+b^2-2ab\cos \theta {)}^2$$

はたして、こんな複雑な式が恒等式として成り立つでしょうか？

Wolfram Alpha先生による検算 の結果、ナント「真」と判定されました！

まとめ

このカラクリが気になって夜しか眠れないって方は、 ガラパゴ三辺比定理 を参照してみてね(*´ω｀*)