パンツ分解を与える曲線について
2回目の投稿です。
今回は、曲面のパンツ分解を与える単純閉曲線の族について書きたいと思います。
自分の勉強のために書いているので、誤りを多く含む可能性が高いです。
設定
$S$は向き付けられた連結な種数$g$が$2$以上の閉曲面とします。このとき、$S$には断面曲率$-1$のリーマン計量が定まります。このようなリーマン計量$\sigma$をとっておきます。リーマン多様体$M=(S,\sigma)$には、等温座標系を考えることでリーマン面の構造が入ります。$\mathscr{S}$を$M$上の自明でない単純閉曲線の自由ホモトピー類全体の集合とします。$[\gamma],[\delta] \in \mathscr{S}$が互いに交わらないとは、$[\gamma]\neq[\delta]$であり、ある元$\gamma' \in [\gamma]$,$\delta' \in [\delta]$が存在して、$\gamma'\cap \delta' =\emptyset$となることとします。
リーマン面$M$のパンツ分解とは、$M$を単純閉測地線で切り取っていって、各連結成分がパンツ(=$S^2$から円盤を$3$つくり抜いたもの)になるようにすることです。
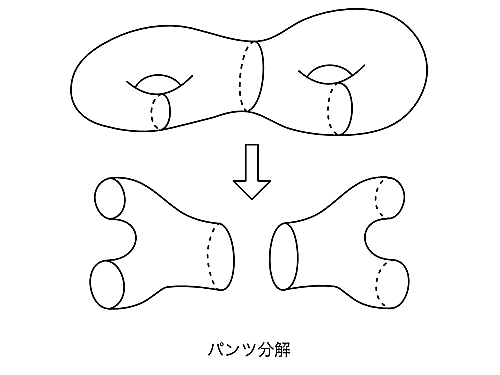 パンツ分解
パンツ分解
主張と準備
主張
今回示したいことは以下の命題です。
$\{\gamma_1,\cdots,\gamma_n\}$を$M$上の互いに交わらない単純閉測地線の族とする。このとき、次は同値である。
- $\{\gamma_1,\cdots,\gamma_n\}$は$M$のパンツ分解を与える。
- $\{\gamma_1,\cdots,\gamma_n\}$は互いに交わらない単純閉測地線の族として、極大なものである。
- $n=3g-3$である。
この命題から、任意に与えられた閉測地線$\gamma$から、$\gamma$に交わらないその閉測地線を次々と取っていくことで、$\gamma$を含むようなパンツ分解を与える閉測地線の族を構成することができます。
準備
トポロジカルな話に帰着する
本命題を示すにあたって、次の命題は認めることにします。
任意の$[\gamma] \in \mathscr{S}$に対して、測地的代表元$\gamma' \in [\gamma]$がただ1つ存在する。
トポロジカルな話に帰着したいので、次の命題を示します。
$[\gamma],[\delta] \in \mathscr{S}$が互いに交わらないとき、測地的代表元$\gamma' \in [\gamma],\delta' \in [\delta]$は互いに交わらない。
$\gamma'$と$\delta'$が互いに交わっていたとする。これらは、互いに交わらない単純閉曲線からの連続変形で得られることから、交点のでき方はbigonを作るようなでき方しか有り得ない。$\gamma'$と$\delta'$の交点のうち、bigonを作っている$2$頂点を$p,q$とし、bigonをなす$\gamma',\delta'$の部分弧をそれぞれ、$\gamma'|_{pq}$,$\delta'|_{pq}$とする。このとき、$\gamma'|_{pq}$は$\delta'|_{pq}$にホモトピックである。$p,q$を端点に持つ曲線のホモトピー類の中で、測地線は一意であるから、$\gamma'|_{pq}=\delta'|_{pq}$ということになり、測地線の伸ばし方は一意であるから、$\gamma'=\delta'$となる。しかし、これは$[\gamma]$と$[\delta]$が互いに交わらないことに矛盾。
ちなみに、bigonとは図のような二角形のことです。
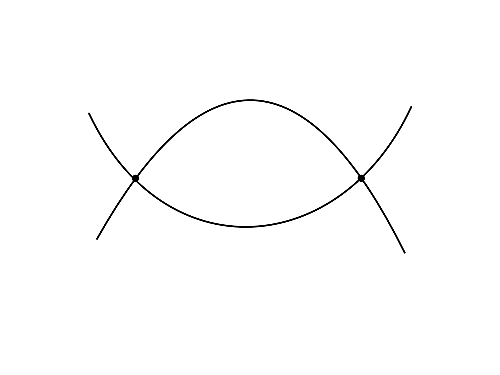 bigon
bigon
したがって、命題1において、単純閉測地線の部分を単純閉曲線(の自由ホモトピー類)に置き換えたものを示せばよいです。:互いに交わらない単純閉曲線で議論し、命題2により、それらを測地線に伸ばしてあげます。そして、命題3より伸ばしてあげたあとも、それらは互いに交わらないからです。
オイラー標数の加法性
$P$を連結な向き付けられたコンパクトな曲面としましょう。(境界付きも含む)$P$を単純閉曲線で切って$P_1,P_2$に分かれたとします。このとき、オイラー標数の包除原理から、
$$\chi(P)=\chi(P_1)+\chi(P_2)-\chi(S^1)=\chi(P_1)+\chi(P_2)$$
が成り立ちます。これをオイラー標数の加法性と呼ぶことにします。
証明
(1.$\Rightarrow$3.) まず、パンツ分解を与える閉曲線の本数は$3g-3$本であることを示す。$M$が$m$個のパンツ$P_1,\cdots,P_m$に分解されたとすると、パンツのオイラー標数は$-1$なので、オイラー標数の加法性から、
$$ 2-2g = \chi(M) = \chi(P_1) + \cdots + \chi(P_m)=-m$$
となる。したがって、$m=2g-2$がわかる。単純閉曲線で切るごとに、境界成分は2つ増える。最終的に、境界成分は$3\times(2g-2)=6g-6$個できる。したがって、パンツ分解をするためには$(6g-6)\div2=3g-3$回切ることが必要である。したがって、$n=3g-3$である。
(2.$\Rightarrow$1.) $\{\gamma_1,\cdots,\gamma_n\}$を互いに交わらない単純閉曲線の族で、極大なものとする。これらの曲線で、曲面$M$を切ったときに、得られる曲面の連結成分をそれぞれ$P_1,\cdots,P_m$とする。これらが、すべてパンツならば、話は終わるので、パンツでないような曲面$P_i$があるとする。すると、$P_i$は閉曲面の分類定理から、種数が$1$以上の閉曲面から円板を取り除いて得られる曲面か、球面から円板を$4$つ以上取り除いて得られる曲面のいずれかである。なぜなら、$M$を単純閉曲線で切って得られる曲面はすべてオイラー標数が負になることが必要だからである。
(オイラー標数が非負であるような曲面で、出て来る可能性があるのは、球面、円盤、トーラス、シリンダーであるが、球面とトーラスは境界が無いので有り得ず、円盤が出て来るときは自明なループで切ったときであり、シリンダーが出てきたら、ホモトピー同値なループで切ってしまっているということになるからである。)
しかし、このとき$P_i$から、明らかに非自明なループで境界成分にホモトピックでないものが取れてしまうことになり、$\{\gamma_1,\cdots,\gamma_n\}$が極大なものであることに反する。したがって、$P_1,\cdots,P_m$はすべてパンツである。
(3.$\Rightarrow$2.) $\Gamma=\{\gamma_1,\cdots,\gamma_{3g-3}\}$を条件を満たすループの族とする。$\Gamma'$を$\Gamma \subset \Gamma'$となるような曲線の族で極大なものとする。このとき、(2.$\Rightarrow$1.)より、$\Gamma'$はパンツ分解を与える。(1.$\Rightarrow$3.)より$|\Gamma'|=3g-3$である。したがって、$\Gamma=\Gamma'$である。
こうして、「$\Rightarrow$」が三角形を成すような感じで証明ができました
参考文献
- [F,M] B.Farb, D.Margalit: A Primer on Mapping Class Groups, Princeton University Press