Whitneyの例 ~分類の障壁~
どうも,小脳に委縮が見られていると診断されたえだまめです.いやぁ,二か月も頭を使わないと委縮するもんなんですねぇ…委縮して理性飛んだか?って言ったら知り合いの心理学科の先生に「それは素朴科学的観点で脳の容量が知力に直結するって意見だが,その関連性はまだ示されていない」って指摘されちゃいました.たしかになぁ~って感じですよねw
さて,今回は特異点論チックな記事を書こうと思います.簡単に探したら日本語記事が見当たんなかったので残しておこうという次第です(正確にはうちの先生がpdfを残してるのを知ってるんですが見つからないし難しい!).
簡単にまとめると,簡単な特異点を持つ写像をその周りでの表示で分類してしまおう!という考えがあるのですが,複雑度が増すと有限個の分類じゃ効かなくなってくるという話です.その簡単な分類はまた今度記事にするかもしれないですが,今回は複雑な場合から紹介しちゃいます.
前提知識は多様体のヤコビ行列がとりあえずすごい!くらい知っとけば読めると思います.
まずは分類の仕方から.
$f,g:\mathbb{R}^2\rightarrow\mathbb{R}$が$\mathcal{R}$-同値
$\def$ $^\exists\varphi:\mathbb{R}^2\rightarrow\mathbb{R}^2$を$C^{\infty}$級微分同相写像 s.t. $f=g\ \circ\varphi$
またこのとき,$f\sim_{\mathcal{R}}g$と表記する.
基本的に特異点論では関数を定義域に依らず($\mathbb{R}^n$とかその中の開集合の意)この同値類で分類していくことが多い.例えば$\dim _{\mathbb{R}} \mathbb{R}[[x,y]]/\langle f_x,f_y\rangle \leq 5$なら(念のため偏微分です.突然出てきてビビるだろうがよくこの指標を使う.余次元/codimensionという.そのうち解説を出すと思うが早く知りたい人は後輩の記事を読めばいいだろう. https://mathlog.info/articles/VOWuzfTUFfqItCDyAxB0 ミルナー数周りの話だ)以下の表のどれかに$\mathcal{R}$-同値である.
| 関数 | 余次元 | 名称 |
|---|---|---|
| $x$ | 0 | $A_0$/レギュラー |
| $x^2\pm y^2$ | 1 | $A_1$ |
| $x^3 + y^2$ | 2 | $A_2$ |
| $x^4\pm y^2$ | 3 | $A_3$ |
| $x^5+y^2$ | 4 | $A_4$ |
| $x^6 \pm y^2$ | 5 | $A_5$ |
| $x^3 + y^3$ | 4 | $D_4^+$ |
| $x^3 - xy^2$ | 4 | $D_4^-$ |
| $x^2y+y^4$ | 5 | $D_5$ |
これより悪いような,余次元が大きい特異点もArnold先生がSingularities of Differentiable Mapsで分類をあたえられている.特異点の研究者はこぞってこれを参照すのだとかw僕も先生にこれ読めと勧められたものだ.もちろん,全部は読めないw
系列は次のようになる.要は特異点の悪さの順だ.矢印が進めば進むほど悪くなる.余次元との関係の言及は他のところでするだろう.……たぶん.
 単純特異点の悪さ
単純特異点の悪さ
またこれらの特異点を持つ関数の0点ファイバーは以下となる.
![!FORMULA[29][36345583][0]の図](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FOK8pDw7n8EMK7XWSAqFt.jpg?alt=media) $f=0$の図
$f=0$の図
さて,本題に入ろう.
$f_t=xy(x-y)(x-ty)$と置く.$0< s,t<\frac{1}{2}$をとる.このとき,以下が成立する.
$$f_s \sim_{\mathcal{R}} f_t \ \Longleftrightarrow \ s=t$$
示す前に定理の意味を考える.$s$と$t$が一致しない時,$f_s$と$f_t$は$\mathcal{R}$-同値になり得らない.つまり,その濃度分だけ$\mathcal{R}$-同値でないものが出てくるということである.分類するなら有限個であってほしいのでこれは大問題である.
また試しに$\dim _{\mathbb{R}} \mathbb{R}[[x,y]]/\langle f_{\frac{1}{4},x},f_{\frac{1}{4},y} \rangle$ を計算してみると,
$$\mathbb{R}[[x,y]]/\langle f_{\frac{1}{4},x},f_{\frac{1}{4},y}\rangle \cong \langle 1,x,x^2,y,xy,y^2,xy^2,y^3,y^4 \rangle_{\mathbb{R}}$$
らしいので(Singularというソフトで計算できる),余次元が9になる.高々有限なのに分類が上手くいかないなんて言語道断である.いや,特異点扱ってるからしゃーないんだけど.
では,意義も説明できたと思うので証明に移ろう.その準備で定義と補題を用意する.
4個の実2次元ベクトル$v_1,v_2,v_3,v_4$をとる.このとき,非調和比$\sigma_{1,2,3,4}$を以下で定義する.
$\sigma_{1,2,3,4}=|v_1,v_3||v_2,v_4|/|v_2,v_3||v_1,v_4|$
非調和比$\sigma_{i,j,k,l}$をとる.ここで$\{i,j,k,l\} = \{1,2,3,4\}$とする.このとき,以下が成立する.
(i) $\sigma_{1,2,3,4} = \frac{1}{\sigma_{2134}}$,$\sigma_{1,2,3,4} = \frac{1}{\sigma_{1,2,4,3}}$
(ii) $\sigma_{1,2,3,4} = \sigma_{2,1,4,3} = \sigma_{3,4,1,2} = \sigma_{4,3,2,1}$
(iii) $\{\sigma_{i,j,k,l} \ |\ \{i,j,k,l\}=\{1,2,3,4\} \} = \{ \sigma_{1,2,3,4},\sigma_{1,2,4,3},\sigma_{1,3,2,4},\sigma_{1,3,4,2},\sigma_{1,4,2,3},\sigma_{1,4,3,2} \}$
非調和比に対応するベクトルを$v_1,v_2,v_3,v_4$とする.
$\underline{\text{(i) について }}$
$$\frac{1}{\sigma_{1,2,4,3}} = |v_2,v_4||v_1,v_3|/|v_1,v_4||v_2,v_3| = \sigma_{1,2,3,4}$$
$\sigma_{1,2,4,3}$の方も同様.
$\underline{\text{(ii) について }}$
$$\begin{array}{rcl}
\sigma_{2,1,4,3} &=& |v_2,v_4||v_1,v_3|/|v_2,v_3||v_1,v_4|\\
\sigma_{3,4,1,2} &=& |v_3,v_1||v_4,v_2|/|v_3,v_2||v_4,v_1| \\
\sigma_{4,3,2,1} &=& |v_4,v_2||v_3,v_1|/|v_4,v_1||v_3,v_2|
\end{array}$$
より,すべて$\sigma_{1,2,3,4}$に一致する.符号に関しては相殺されることに注意したい.
$\underline{\text{(iii) について }}$
(ii)より$4!=24$通りある並び通りのうち1つ当たり4個の等しい非調和比のセットが作れるため$24/4=6$個以下の要素があることが予想される.これが互い違いになるかは後ろの定理の証明で見てみよう.
(i) 0ではない定数$c_i\ (i=1,2,3,4)$に対して,
$$\sigma(c_1v_1,c_2v_2,c_3v_3,c_4v_4) = \sigma(v_1,v_2,v_3,v_4)$$
(ii) $2\times 2$の正則行列$A$に対して,
$$\sigma(Av_1,Av_2,Av_3,Av_4) = \sigma(v_1,v_2,v_3,v_4)$$
$\underline{\text{(i) について }}$
$\begin{array}{rcl}
\sigma(c_1v_1,c_2v_2,c_3v_3,c_4v_4) &=& |c_1v_1,c_3v_3||c_2v_2,c_4v_4|/|c_2v_2,c_3v_3||c_1v_1,c_4v_4|\\
&=& c_1c_2c_3c_4|v_1,v_3||v_2,v_4|/c_1c_2c_3c_4|v_2,v_3||v_1,v_4|\\
&=& \sigma(v_1,v_2,v_3,v_4)
\end{array}$
$\underline{\text{(ii) について }}$
まず以下のことを示そう.
$$|Av_1,Av_2|=|A||v_1,v_2|$$
行列の積と行列式は交換可能なため直ちに従う.よって
$$\begin{array}{rcl}
\sigma(Av_1,Av_2,Av_3,Av_4) &=& |A|^2|v_1,v_3||v_2,v_4|/|A|^2|v_2,v_3||v_1,v_4|\\
&=& \sigma(v_1,v_2,v_3,v_4)
\end{array}$$
では準備もできたので,証明していこう.
$f_s \sim_{\mathcal{R}} f_t$を仮定する.
このとき次の$C^\infty$-微分同相写像$h:\mathbb{R}^2\rightarrow \mathbb{R}^2$が存在して,$f_s \ \circ h = f_t$となる.よって,$h(f_t^{-1} (0))) = f_t^{-1}(0)$となる.つまり0の逆像が$h$を噛ませることで一致する.
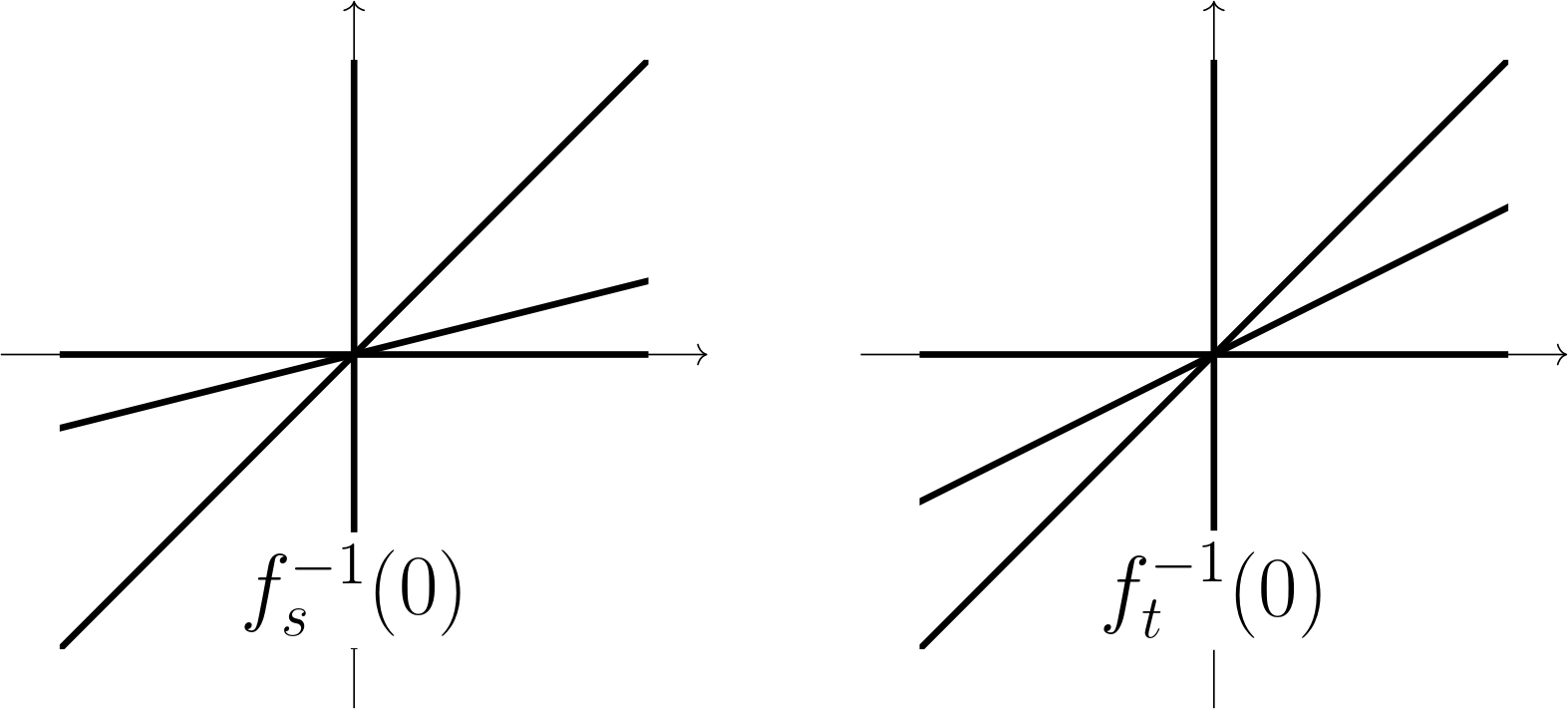 逆像のグラフ
逆像のグラフ
このことから$dh_{(0,0)}(f_t^{-1}(0)) = f_t^{-1}(0)$が成り立つ.これはこの四本に伸びる直線がそれぞれの直線らに写ることを示している.つまり,4個の実2次元ベクトル
$$\DVec{1}{0}, \ \DVec{0}{1}, \ \DVec{1}{1},\ \DVec{t}{1}\ \ \ \ \ \ (1-1)$$
は正則行列$J_h(0,0)$($h$のヤコビ行列)によって,$c_i \not = 0 \ (i=1,2,3,4)$を用いて4個の実2次元ベクトル
$$c_1 \DVec{1}{0}, \ c_2 \DVec{0}{1}, \ c_3 \DVec{1}{1},\ c_4 \DVec{s}{1}\ \ \ \ \ \ (1-2)$$
のいずれかに写される.ここからのトリックでんえぇ?となるが非調和比を使う.4個の実2次元ベクトル
$$\DVec{1}{0}, \ \DVec{0}{1}, \ \DVec{1}{1},\ \DVec{t}{1}$$
で決まる非調和比を
$$\sigma(t) = \left| \begin{array}{cc}
1& 1\\
0 &1
\end{array} \right| \left| \begin{array}{cc}
0 & t\\
1 & 1
\end{array} \right| \left/
\left| \begin{array}{cc}
0 & 1\\
1 & 1
\end{array} \right|
\left| \begin{array}{cc}
1 & t\\
0 & 1
\end{array} \right|
\right.
=t$$
とし,$\sigma(s)_{ijkl} = \sigma (v_i,v_j,v_k,v_l)(s)\ \ \ (i,j,k,l=1,2,3,4)$を4つのベクトル
$$v_1=\DVec{1}{0}, \ v_2=\DVec{0}{1}, \ v_3=\DVec{1}{1},\ v_4=\DVec{s}{1}$$
で決まる非調和比と補題3(1)から式(1-1)らのベクトルが式(1-2)のベクトルらに正則行列$J_h(0,0)$で写る.この非調和比は補題3(2)より保たれる.また,実係数がついても非調和比が補題3(1)より保たれるため$\sigma(t)$と$\sigma(s)_{i,j,k,l}$が一致することが分かる.
補題2(3)より非調和比を計算していくと,
$$\begin{array}{ccccc}
\sigma(s)_{1,2,3,4} &= & \Ratio{1}{1}{0}{1}\Ratio{0}{s}{1}{1}\left/ \Ratio{0}{1}{1}{1}\Ratio{1}{s}{0}{1} \right. & = &s\\
\sigma(s)_{1,2,4,3} &= & \Ratio{1}{s}{0}{1}\Ratio{0}{1}{1}{1}\left/ \Ratio{1}{1}{0}{1}\Ratio{0}{1}{s}{1} \right. & = &\frac{1}{s}\\
\sigma(s)_{1,3,2,4} &= & \Ratio{1}{0}{0}{1}\Ratio{1}{s}{1}{1}\left/ \Ratio{1}{s}{0}{1}\Ratio{1}{0}{0}{1} \right. & = &1-s\\
\sigma(s)_{1,3,4,2} &= & \Ratio{1}{s}{0}{1}\Ratio{1}{0}{1}{1}\left/ \Ratio{1}{0}{0}{1}\Ratio{1}{s}{1}{1} \right. & = &\frac{1}{1-s}\\
\sigma(s)_{1,4,2,3} &= & \Ratio{1}{0}{0}{1}\Ratio{s}{1}{1}{1}\left/ \Ratio{1}{1}{0}{1}\Ratio{s}{0}{1}{1} \right. & = &\frac{s-1}{s}\\
\sigma(s)_{1,4,3,2} &= & \Ratio{1}{1}{0}{1}\Ratio{s}{0}{1}{1}\left/ \Ratio{1}{0}{0}{1}\Ratio{s}{1}{1}{1} \right. & = &\frac{s}{s-1}\\
\end{array}$$
となり,どれかに$t$が一致している.範囲が$0< s,t<\frac{1}{2}$であるからすべてのグラフを描いてみると,
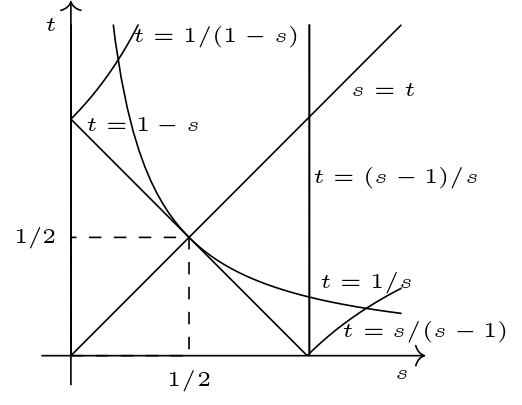 線形計画法
線形計画法
となるが,この中で$s,t$の範囲で適しているのは$s=t$のみである.
このように非調和比を用いて証明が為される.このように分類したときに実数濃度分出てきてしまうものをモジュライと呼ぶ.
またほかの例として$F_s(x,y)=x(y-x^2)(y-sx^2)$としたとき,0点集合として(つまり$\mathcal{K}$-同値)分類するとモジュライが出てきてしまうが関数として分類するとモジュライが出ないらしい.先生が言ってた.証明もめんどくさいとか.
参考
・野口広,福田拓生,”初頭カタストロフィー”
・吉永悦男,福井敏純,泉脩蔵,”特異点の数理3”
・V.I.Arnold,S.M.Gusein-Zade,A.N.Varchenko,"Singularities of Differentiable Maps"
