幾何問題(2)

幾何の問題を出します。ぜひ解いてください！
簡単かもです。

問題

問題
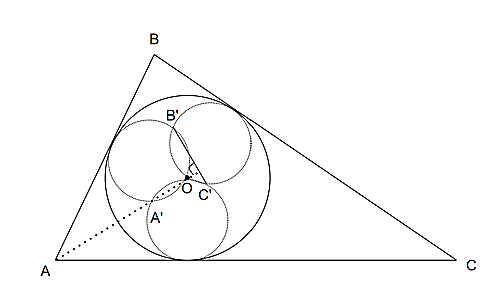
$\triangle ABC $があり、内接円を$\Gamma$の中心を$O$とする。
$\Gamma$と$\triangle ABC$の$3$つの接点と$O$を直径とする円を書き、$2$つの円の交点を上のように$A',B',C'$とすると、

• $A,A',O$は一直線上にあること
• $AA' \perp B'C'$となること

を示せ。