幾何問題(2)を解いてみるよ
はじめに
問題
元の問題とはアルファベットの割り当てが大きく変わっています.
こちらのミスですが注意してください.
$\triangle ABC $において,この三角形の内接円$\Gamma $と$AB,BC,AC$の接点$D,E,F$と$\Gamma$の中心$O$を直径とする円$X,Y,Z$を書き,
$X,Y$の$O$と異なる交点を$A'$
$Y,Z$の$O$と異なる交点を$C'$
$X,Z$の$O$と異なる交点を$B'$
とおくとき,
(1) $B,A',O$は同一直線上にあることを示せ.
(2) 直線$A',O$と$B'C'$は直交することを示せ.
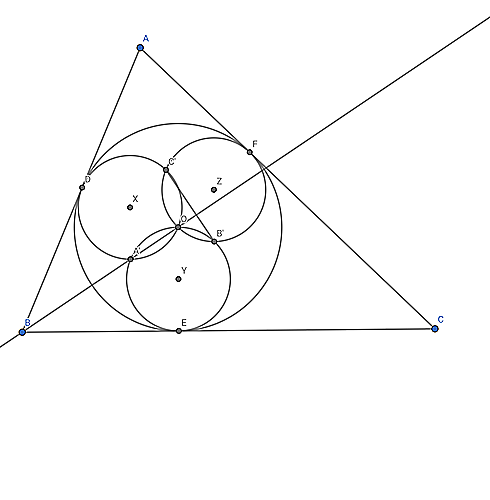 図1
図1
解答
(1)について
$\triangle OA'D , \triangle OA'E$において
明らかに$OD=OE$であって,
円周角の定理より$\angle OA’D= \angle OA’E=90^\circ$であり,$ OA’ $が共通だから
$ \triangle OA’D \equiv \triangle OA’E $(ニ辺他一辺相等)であり,$DA'=EA'$が成立する.
これと$BD=BE$,$A'B$が共通であることから,
$ \triangle A’BD \equiv \triangle A’BE $(三辺相等)から$ \angle BA’D= \angle BA’E $で,
$D,A',E$が同一直線上にあることから$ \angle BA’D= \angle BA’E= 90^{\circ} $
であるから,$ \angle BA’E + \angle OA’E=180^\circ $から$B,A',O$は同一直線上にある.
(2)について
(1)より示すべきものは$ A’O \perp B’C’ $
$C'O$が共通,$OF=OD$,$ \angle OC’D= \angle OC’F= 90^{\circ} $より$ \triangle OC’D \equiv \triangle OC’F $(ニ辺他一辺相等)から
$DF$の中点が$C'$である.同様に
$EF$の中点が$B'$である.
中点連結定理より$ DE /\!/ C’B’ $であり,
明らかに$ DE \perp A’O $から
$ A’O \perp B’C’ $である.よって題意は示された.
おわりに
これはこちらのミスですがアルファベットの割り当てが大きく変わってます.
訂正めんどい
高校入試の難問にありそう
