高校数学の確率の問題のみかた

前提知識 : 確率
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

前置き

先ず, 何故私がこのような記事を執筆するに至ったのか, 少しばかりお話します.

始めに, 私が高校数学の各分野の中で, 最も苦手であると意識を持っているのが「確率」です. 教科書の言っていることは解りやすいのですが, 私の理解は甘いようで, 少し捻られると計算するべき量を誤ってしまうことが多々有ります. そこで, 今回は私の視点から確率という概念をいま一度眺め, 苦手意識を持つ者として, また現代の知恵に対して無知であるような者として, それなりに思考をしてみたという足跡を残してみたく思いたって, このような記事を書いています. そのため, 本記事は高校数学の確率分野を一通り学んだのに, 何だかもどかしい, 定義に忠実に従えているか不安を感じるという方に特に向いているかも知れません.

記事の構成については迷う所が有ったのですが, 結局は, 幾つかの問題を「ゆっくり」解くという方法にしました. 確率分野への理解のためにはとても大切な考え方であるように思うので, 宜しければ最後までお付きあいください.

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

一つ目の問題と解答

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

誤解

赤旗が見えているため北か西かの二択であり, 答えの確率は$1/2$, としては誤りである. 何故ならば, 北の塔の旗の赤面を見た確率と西の塔の旗の赤面を見た確率を比べては, 赤面が二つ有る西の塔の旗のほうが確率が大きく, これらは同様に確からしくないからである. より細かく, 全てが同様に確からしい根元事象にまで分割してから確率を計算しなければならない.

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

解答

事象$A$が起こる確率を$P(A)$で表す.

区別をするため, それぞれの旗に表裏を定める. 北の塔の旗については白塗りを表, 赤塗を裏と限定するが, 東の塔の旗および西の塔の旗については何れを表, 何れを裏と決めても差しつかえない.

与えられた条件から, 東の塔の旗の表面を見る事象, 東の塔の旗の裏面を見る事象, 北の塔の旗の表面を見る事象, 北の塔の旗の裏面を見る事象, 西の塔の旗の表面を見る事象, 西の塔の旗の裏面を見る事象をそれぞれ$A_1,A_2,B_3,B_4,C_5,C_6$で表せば, 集合$\mathbb{A}=\{A_1,A_2,B_3,B_4,C_5,C_6\}$の要素は根元事象と見なせる. 即ち,
$$ \begin{align} P(A_1)=P(A_2)=\cdots=P(C_6)\quad\mbox{かつ}\quad P(A_1)+P(A_2)+\cdots+P(C_6)=1 \end{align} $$が成りたつ. この$6$個の要素の中で
$$ \begin{align} \begin{array}{c} \mbox{赤旗を見ていて, かつ, 西の方角を見ている事象の個数}\\\hline \mbox{赤旗を見ている事象の個数} \end{array} \end{align} $$なる割合を計算すれば良いが, 分子に該当するのは$C_5,C_6$の$2$つ, 分母に該当するのは$B_4,C_5,C_6$の$3$つであるから, 答えの確率は$2/3$である.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

二つ目の問題と解答

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

長い解答

事象$A$が起こる確率を$P(A)$で表す.

与えられた条件から, 確率に関する一部を書きかえる. 以下のそれぞれは, 硬貨の表と裏が何れも$1/2$の確率で出るということ, 　証言者の一人目が$4/5$の確率で本当のことを言うということ, 証言者の二人目が$4/5$の確率で本当のことを言うということをそれぞれ表現している.

• 「硬貨を投げたとき, ある事象の集合$\mathbb{A}=\{A_h,A_t\}$が存在して, その要素は根元事象である. 即ち,
  $$ \begin{align} P(A_h)=P(A_t)\quad\mbox{かつ}\quad P(A_h)+P(A_t)=1 \end{align} $$が成りたつ. 」

• 「硬貨を投げたとき, ある事象の集合$\mathbb{B}=\{B_1,B_2,B_3,B_4,B_5\}$が存在して, その要素は根元事象である. 即ち,
  $$ \begin{align} P(B_1)=P(B_2)=\cdots=P(B_5)\quad\mbox{かつ}\quad P(B_1)+P(B_2)+\cdots+P(B_5)=1 \end{align} $$が成りたつ. 」

• 「硬貨を投げたとき, ある事象の集合$\mathbb{C}=\{C_1,C_2,C_3,C_4,C_5\}$が存在して, その要素は根元事象である. 即ち,
  $$ \begin{align} P(C_1)=P(C_2)=\cdots=P(C_5)\quad\mbox{かつ}\quad P(C_1)+P(C_2)+\cdots+P(C_5)=1 \end{align} $$が成りたつ. 」

ここで, 確率の計算に当たって考えるべき根元事象は, 全ての場合
$$ \begin{align} \mathbb{E}=\{X\cap Y\cap Z\mid X\in\mathbb{A},\ Y\in\mathbb{B},\ Z\in\mathbb{C}\} \end{align} $$であり, この$2\times5\times5$個の要素の中で
$$ \begin{align} \begin{array}{c} (\mbox{二人が「表が出た」と言い, かつ, 本当に表が出る事象の個数})\\\hline (\mbox{二人が「表が出た」と言う事象の個数}) \end{array} \end{align} $$なる比率を条件付き確率として計算するのであるが, 議論の整合性の明瞭化のため,
$$ \begin{align} \begin{array}{l} \mathbb{D}=\{Y\cap Z\mid Y\in\mathbb{B},\ Z\in\mathbb{C}\}\quad(5\times5\mbox{個の事象の集合}),\\ \mathbb{E}=\{X\cap W\mid X\in\mathbb{A},\ W\in\mathbb{D}\}\quad(2\times5\times5\mbox{個の事象の集合}) \end{array} \end{align} $$のように二段階にして起こりうるものを場合分けしてゆく.

$5\times5$個の事象の積
$$ \begin{align} B_1\cap C_1,\ B_1\cap C_2,\ \ldots,\ B_i\cap C_j,\ \ldots,\ B_5\cap C_4,\ B_5\cap C_5 \end{align} $$をこの順に$D_1,\ D_2,\ \ldots,\ D_{25}$と名づけると, これらは集めると根元事象と成る. 即ち,
$$ \begin{align} P(D_1)=P(D_2)=\cdots=P(D_{25})\quad\mbox{かつ}\quad P(D_1)+P(D_2)+\cdots+P(D_{25})=1 \end{align} $$が成りたつ. $D_1,\ D_2,\ \ldots,\ D_{25}$の各々は二人の証言人の言ったことの真偽を纏めて表すが, 一人目が真かつ二人目が真, 一人目が真かつ二人目が偽, 一人目が偽かつ二人目が真, 一人目が偽かつ二人目が偽の$2\times2$通りのみでないのは, これらの$4$通りは同様に確からしからず, 根元事象として扱えないからである.

続いて, $25\times2$個の事象の積
$$ \begin{align} &A_h\cap D_1,\ A_h\cap D_2,\ \ldots,\ A_h\cap D_{25},\ \\ &A_t\cap D_1,\ A_t\cap D_2,\ \ldots,\ A_t\cap D_{25} \end{align} $$をこの順に$E_1,\ E_2,\ \ldots,\ E_{50}$と名づけると, これらは集めると根元事象と成る. 即ち,
$$ \begin{align} P(E_1)=P(E_2)=\cdots=P(E_{50})\quad\mbox{かつ}\quad P(E_1)+P(E_2)+\cdots+P(E_{50})=1 \end{align} $$が成りたつ.

問題文で与えられた情報から, 事象をこれよりも細かく場合分けする必要は無い.

答えるべきは確率
$$ \begin{align} \begin{array}{c} (E_1,\ E_2,\ \ldots,\ E_{50}\mbox{の中で二人が「表が出た」と言い, かつ, 本当に表が出る事象の個数})\\\hline (E_1,\ E_2,\ \ldots,\ E_{50}\mbox{の中で二人が「表が出た」と言う事象の個数}) \end{array} \end{align} $$であった.

分子は, 本当に表が出る事象$E_1,\ E_2,\ \ldots,\ E_{25}$の中で二人が「表が出た」と真実を言うような事象の個数であるから,
$$ \begin{align} 4\times4=16 \end{align} $$に等しい. 具体的に挙げると,
$$ \begin{align} \begin{array}{llll} E_1,&E_2,&E_3,&E_4,\\ E_6,&E_7,&E_8,&E_9,\\ E_{11},&E_{12},&E_{13},&E_{14},\\ E_{16},&E_{17},&E_{18},&E_{19} \end{array} \end{align} $$の$16$個である.

分母について, 裏が出たときには表が出たときと真実は逆転するから, 二人の各々が「表が出た」と言うことは本当から嘘に変わり, 確率も$4/5$から$1/5$へ減少する. 故に,
$$ \begin{align} &(E_1,\ E_2,\ \ldots,\ E_{25}\mbox{の中で二人が表が出たと真実を言う事象の個数}),&\\ &(E_{26},\ E_{27},\ \ldots,\ E_{50}\mbox{の中で二人が表が出たと嘘を言う事象の個数}) \end{align} $$と二つに分割し, それぞれで個数を計算すると
$$ \begin{align} 4\times4+1\times1=17. \end{align} $$具体的に挙げると,
$$ \begin{align} \begin{array}{llll} E_1,&E_2,&E_3,&E_4,\\ E_6,&E_7,&E_8,&E_9,\\ E_{11},&E_{12},&E_{13},&E_{14},\\ E_{16},&E_{17},&E_{18},&E_{19},\\ E_{50}&&& \end{array} \end{align} $$の$17$個である.

以上から, 答えは$16/17$.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

面積としての解釈

確率をある図形の面積としての割合と見れば, 全事象の表す図形の面積を$1$として, ある事象の起こる確率はある図形の面積としてそのまま表現することができる.

例えば, 表と裏が何れも$1/2$の確率で出る硬貨を投げる全事象の確率を, 一辺長が$1$の正方形$ABCD$の面積として表せば, 硬貨の表が出る事象$A_h$の確率は, 辺$AB$と辺$CD$の中点$M,N$を取って長方形$AMND$の面積として, 硬貨の裏が出る事象$A_t$の確率は長方形$MCDN$の面積として捉えることができる.

先ほどの事象の集合
$$ \begin{align} &\mathbb{D}=\{D_1,\ D_2,\ \ldots,\ D_{25}\},\\ &\mathbb{B}=\{B_1,\ B_2,\ \ldots,\ B_5\},\\ &\mathbb{C}=\{C_1,\ C_2,\ \ldots,\ C_5\} \end{align} $$は何れも根元事象の集まりであったが, 全事象を一辺長が$1$の正方形, 各要素である事象をこの正方形を分割する長方形として表せば下の図のように書ける.
面積による表現

続いて, 全事象を面積が$1/2$の正方形二つ, 根元事象$E_1,\ E_2,\ \ldots,\ E_{50}$を面積が$1/50$の正方形として描き,
$$ \begin{align} E_1,\ E_2,\ \ldots,\ E_{50}\mbox{の中で二人が「表が出た」と言い, かつ, 本当に表が出る事象} \end{align} $$の部分に色を塗ると下の図のように成る.

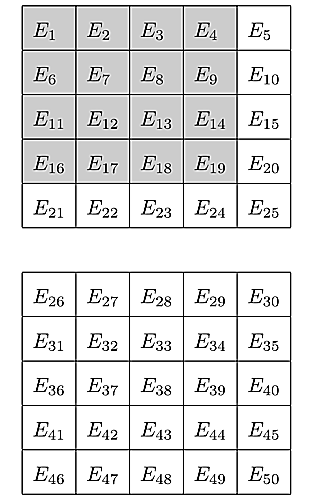分子の表現

同じ図形にて,
$$ \begin{align} E_1,\ E_2,\ \ldots,\ E_{50}\mbox{の中で二人が「表が出た」と言う事象の個数} \end{align} $$の部分に色を塗ると下の図のように成る.

分母の表現

これらの図に従っても, 答えるべき確率は面積の比率として
$$ \begin{align} \frac{16/25}{17/25}=\frac{16}{17} \end{align} $$と算出できる.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

短い解答

硬貨を投げたとき, 表が出る事象を$A$, 二人がともに「表が出た」と言う事象を$B$と書くと, 答えるべき確率は,
$$ \begin{align} P_{B}(A)&=\frac{P(A\cap B)}{P(B)}\\ &=\frac{P(A)P_A(B)}{P(A)P_A(B)+P(\bar{A})P_\bar{A}(B)}\\ &=\frac{\dfrac{1}{2}\times\left(\dfrac{4}{5}\right)^2}{\dfrac{1}{2}\times\left(\dfrac{4}{5}\right)^2+\dfrac{1}{2}\times\left(\dfrac{1}{5}\right)^2}\\ &=\frac{16}{17}. \end{align} $$但し, $\bar{A}$は$A$の余事象を, $P_A(B)$は$A$が起こったという制限の下での$B$の起こる条件付き確率を表す.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

纏め

簡潔に要約して, 以下の教訓に纏めておきます.

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$