二変数関数の極限　〜極限の順序〜

はじめに

今回は、二変数関数$f(x,t)$の極限において、
$$ \lim_{x\to a}\lim_{t\to b}f(x,t)=\lim_{t\to b}\lim_{x\to a}f(x,t) $$
が成り立つのはどういうときなのか、ということについてのイメージの仕方をお話ししていきます。

極限を捉え直す

$$ \lim_{x\to a}f(x)=c $$
とは、任意の$\epsilon>0$に対して
$$ x\in U(a,\delta)\Rightarrow |f(x)-c|<\epsilon $$
を満たす$\delta$をとることができる、ということでした。これは、$x$が然るべき条件$C:x\in U$を満たせば、$\epsilon$の差を除いて$f(x)$と$c$は等しい、と捉えることができます。これを、
$$ f(x)\overset{\epsilon}{=}c $$
と書くことにします。($U$は十分条件としてその部分集合で代用できるので、$U$の取り方は一意的ではありません。)
上の極限を取るという操作を、「$x$を$a$に限りなく近づけることで、$f(x)$を$c$に限りなく近づける」と考えるのではなく、「$x$を$U$に入れることで、$f(x)$を$c$に$\epsilon$より近づける」と考えるのです。議論の途中で$\epsilon$に条件を課すことがなければ、すなわち任意の$\epsilon>0$で成り立つことしか行わなければ、これは結局、
$$ \lim_{x\to a}f(x)=c $$
と読み直せるので、とりあえずは「$\epsilon$の差を除いて等しい」状態で考えよう、というわけです。

関数族の極限

今の話を、関数族$(f_t(x))_{t\in T}$に適用してみます。これは、二変数関数$f(x,t)$を考えることに同じです。以下、$x$の定義域を$X=[0,a)$、$t$の定義域を$T=[0,b)$とします。
$$ \lim_{t\to b}f(x,t)=f(x) $$
に、上の話をとりあえず当てはめてみると、$t$が然るべき条件を満たすとき、
$f(x,t)\overset{\epsilon}{=}f(x)$となります。しかし、$t$の条件は$x$による可能性があるので、次のようにするのがよいでしょう。

いちいち「然るべき条件」というのは面倒なので、この条件は$xt$平面上の領域とみなせますから、それを$\epsilon$領域と呼ぶことにしましょう。$\epsilon$領域内で、$f(x,t)\overset{\epsilon}{=}f(x)$と考えるということです。

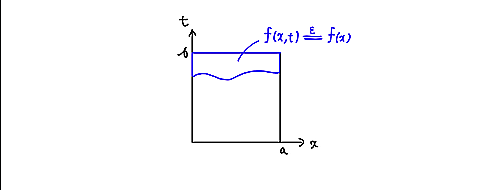epsilon領域

一様収束

$f(x,t)$が$f(x)$に$t\to b$で一様収束するというのは、$\epsilon$領域が次の図のように、長方形に取れるというのと等しいことがわかると思います。

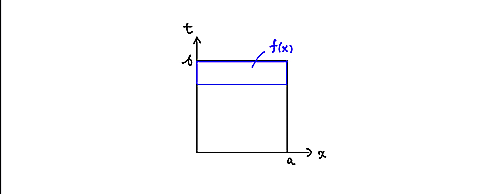一様収束

反対に、$f(x,t)$が$f(x)$に$t\to b$で一様収束せず各点収束するというのは、$\epsilon$領域が次の図のように、定義域内で無限に細くなってしまうということです。

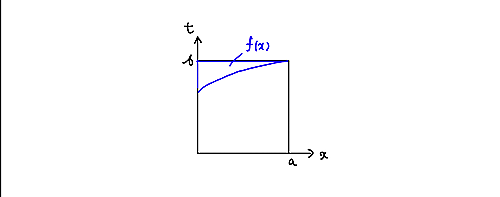各点収束

完全に潰れてしまう点$(a,b)$は定義域の外にあることに注意してください。でないと、各点収束すらしないことになってしまいます。

極限の順序交換

わざわざこのような言い換えをしてきたのは、極限の順序交換の話をするためです。
$$ \lim_{x\to a}\lim_{t\to b}f(x,t)=\lim_{t\to b}\lim_{x\to a}f(x,t)\ ...(A) $$
は一般に成り立つでしょうか。ただし、$\lim_{x\to a}f(x,t)=g(t)$や$\lim_{t\to b}f(x,t)=f(x)$は、少なくとも各点収束の意味で存在するとします。また、$\lim_{x\to a}f(x)=c$も存在するとします。
$\lim_{x\to a}f(x,t)=g(t)$や$\lim_{t\to b}f(x,t)=f(x)$が一様収束か否かで場合分けして考えてみましょう。

ともに一様収束の場合

ともに一様収束ならば、２つの$\epsilon$領域、および$c$の$\epsilon$領域は次のようになっているはずです。

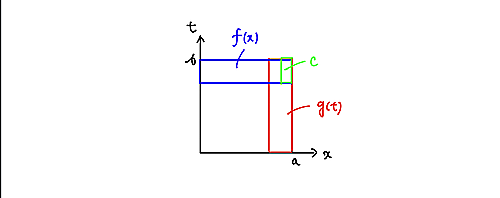ともに一様収束

つまり、$g(t)$の$\epsilon$領域のなかで、$t$を$b$に近づけていけば、$c$の$\epsilon$領域に入ることができます。これは、
$$ \lim_{t\to b}g(t)=c $$
を意味し、$(A)$が成り立つことがわかりました。ついでに、$(a,b)$の近傍で、$c$の$\epsilon$領域にすっぽり入るものが取れますから、
$$ \lim_{(x,t)\to (a,b)}f(x,t)=c\ ...(B) $$
も成り立ちます。

一方のみ一様収束の場合

一方のみ一様収束のとき、２つの$\epsilon$領域、および$c$の$\epsilon$領域は次のようになっているでしょう。

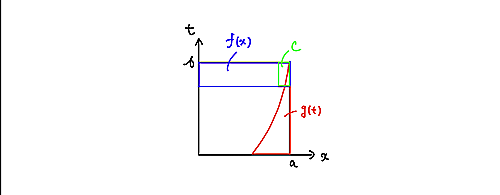一様収束と各点収束

このときもやはり、$g(t)$の$\epsilon$領域のなかで、$t$を$b$に近づけていけば、$c$の$\epsilon$領域に入ることができます。つまり$(A)$は成り立ちますし、同様にして$(B)$も成り立ちます。

ともに一様収束でない場合

ともに一様収束でない場合、一番"ヤバイ"のは、$\epsilon$領域が次のようになっているときです。

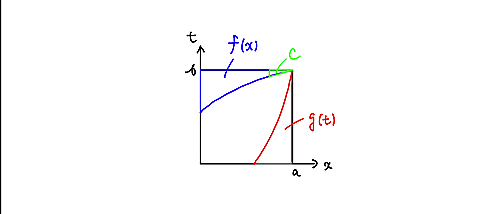ともに各点収束

このとき、$g(t)$の$\epsilon$領域は$c$のそれと共通部分を持たないので、$\lim_{t\to b}g(t)=c$とは限りません。よって$(A)$が成り立つとは言えません。

おわりに

このように、"$\epsilon$領域"というものをイメージすると、極限の順序交換がなぜ一様収束性と関係するのか、少しはわかりやすくなるのではないかと思います。

読んでいただきありがとうございました。