気ままな物理の小文（３）：ビールの泡を科学する

始めに一杯

夏になるとビールがおいしい季節となります。今度ビールを見た折りに、コップにつがれたビールをよく観察してみて下さい。泡がコップの壁からポコポコと現れて、上にあがって行くのが見られるでしょう。普段、何気なく通り過ぎてしまう現象ですが、良くみると興味深い性質があることに気づきます。ビールに溶けている二酸化炭素は溶けている状態より、気体でいる状態の方がより安定です。では何故いっきに気化せずにポコポコと泡が発生するのでしょうか。また、ビールの中に割箸を突っ込むと割箸の回りから勢いよく泡が発生します。それは、何故でしょうか。

今回は、物理の立場からこれらのことを説明してみることにしましょう。

エネルギーと安定性

まず準備として、図1のようにバネにつながれている物体の運動を考えてみます。バネの自然長を原点にとって、座標$x$をおくと、バネの持つエネルギーは$kx^2/2$で与えられます。エネルギーを位置$x$の関数としてグラフを書くと図のようになります。図の状態では、バネは伸びていて縮もうとしますから、物体は左に動こうとします。

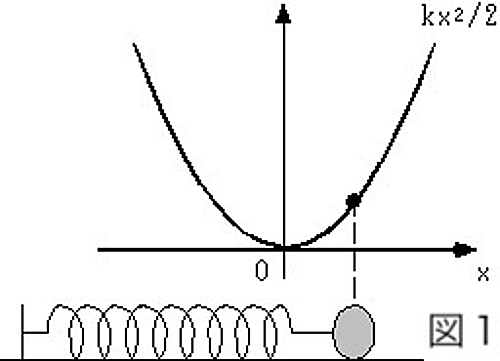fig3-1

これをエネルギーの言葉で考えることもできます。図の状態で物体は左へ動こうとしますが、この時エネルギーは小さくなります。また逆にバネが縮んでいる状態では、バネは伸びようとするので物体は右に動こうとします。この時も、バネのエネルギーは小さくなります。このように、物体の動こうとする方向に対して、次のようなことが言えます。

エネルギーが低い方が安定なので、物体はより安定な状態に行こうとしてエネルギーを小さくしようとする、と見ても構いません。

モデル化

ビールの泡を物理的に扱うには、まずビールの泡の挙動を正しく説明するようなモデルを考える必要があります。また、どのような視点で見るべきかも重要です。ここではエネルギーの視点に立って、モデルを立ててみましょう。

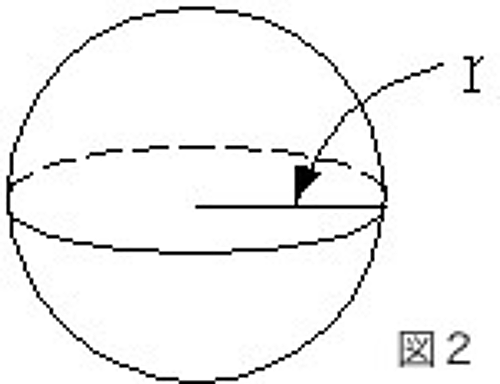fig3-2

ビールに溶けている二酸化炭素は、気化している状態の方がより安定なはずです。ですから、泡が大きければ大きいほどより安定になります。ここで図2のような半径$r$の球形の泡を考えてみましょう。この泡の中にある二酸化炭素の分子の数は、泡の体積$V=4πr^3/3$に比例しています。ですから、半径$r$の泡の持つエネルギー$U_1(r)$は体積$V$に比例して小さくなると考えられ、$r$の関数として次のように表すことが出来そうです。
\begin{equation} U_1(r)=-aV=-\frac{4\pi a}{3}r^3 \end{equation}
ここで$a$は正の比例定数です。前についているマイナスが、「泡の体積が大きいほど安定」なことを示しています。このエネルギーのことを「体積エネルギー」と呼ぶことにしましょう。

先ほど泡を球形であるとしました。我々が目にするビールの泡はほとんどが球形です。泡は何故わざわざ球の形をとるのでしょうか？これは、「液体と気体が接している部分（これを界面といいます）の面積を最小にしようとする性質がある」とすれば説明できます。体積を一定としたとき、表面積が最小となるのは球の時だから、この時が一番安定であるというわけです。

この現象は良く見られます。例えば、雨粒は普通球ですし、宇宙にいって無重力になったとき、水滴は非常にきれいな透明な球となります。また逆に昔の人は鉄砲の弾をつくるに、この性質を利用しました。つまり融かした鉄を高いところから落してやって、落下させながら冷やしてやったのです。そうすると、弾は非常に正確な球の形になってくれるのです。また別の例として、シャボン玉を思い浮かべても良いでしょう。シャボン玉をふくらますと球になりますよね。シャボン玉の場合は薄膜ですが、膜を構成している液体と空気との界面の面積を最小にしようとしている点で、泡と全く同じであるといえます。ですから球状になるわけです。

この界面を最小にしようとする性質を、エネルギーの言葉でいい直してみましょう。界面が存在すると、「界面エネルギー」が存在すると考えます。界面の面積が小さいほど安定なので、その方が界面エネルギーは小さくなるとします。また界面エネルギーは界面の面積に比例するとして良いでしょう。半径$r$の球の表面積$S$は、$S=4πr^2$で与えられます。ですから、半径$r$の泡の持つ界面エネルギー$U_2(r)$は$r$の関数として、次のように表せます。
\begin{equation} U_2(r) = bS = 4\pi b r^2 \end{equation}
ここで$b$は正の比例定数です。$U_1(r)$の時と違って前についている符号は$＋$で、界面の面積$S$が小さい方が安定であることを示しています。（表面エネルギーが界面の面積に比例することは、「表面張力」から説明することが出来ます。それを示していると本題から外れてしまいますので、ここでは扱わないことにします。）

このように考えていくと、泡の性質を考えるには先ほどの体積エネルギー$U_1(r)$に加えて、この界面エネルギー$U_2(r)$も同時に考えなくてはいけないことがわかります。結局、泡のもつエネルギーの合計は、
\begin{equation} U(r) = U_1(r) + U_2(r) = -\frac{4}{3} \pi a r^3 + 4\pi b r^2 \end{equation}
となります。これで、泡のモデルができました。後はこれを元にして、泡の性質を調べていきましょう。

泡の生成のメカニズム

まずエネルギー$U(r)$のグラフを描いてみることにしましょう。$U(r)=0$を解くと$r=0$, $3b/a$であることと、$U(r)$の導関数$U'(r)$を$0$として、関数が極小、あるいは極大になる位置がそれぞれ$r = 0$, $2b/a$であることを用いて、グラフは図3のように描くことが出来ます。（泡の半径は負になることはないので、グラフは$r>0$の範囲のみ示してあります。）このグラフから、いろいろなことを知ることが出来ます。まず、半径を$r=0$から少しずつ増加させていくとエネルギーはしばらく増加していきます。このエネルギーの増加は半径が$r=2b/a$になるまで続きます。これは、半径がまだ小さいうちは、泡の半径が小さい方が安定であることを示しています。よって泡はエネルギーをより小さくするために、萎もうとします。（これは泡の界面の面積を小さくしようとするためです。）

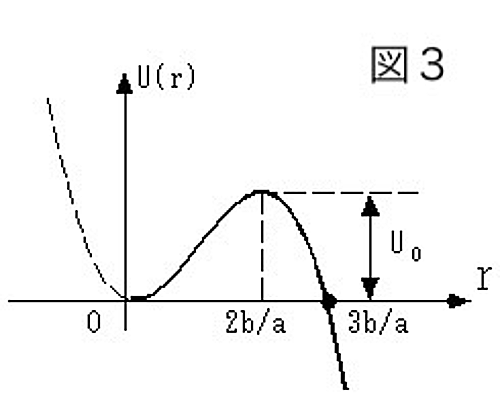fig3-3

ところが、半径が$2b/a$以上になると、今度は半径r が増加するに従って、エネルギーはどんどん小さくなっていきます。この傾向はずっと続きます。よって、半径が$2b/a$より大きい泡はエネルギーをより小さくするために膨らもうとします。（これはもともと二酸化炭素は気化した方が安定だからです。）

このように泡の振舞いは、ある半径を境にして全く異なってきます。この境目の半径$r=2b/a$のことを臨界半径と呼びます。泡の振舞いをまとめると次のようになります。

何かの拍子で泡ができたとしても、その半径が臨界半径より小さくないとダメなのです。

次に泡がどのように生成されるかを考えてみましょう。何にもないところから、半径$r$の泡が出来るためには外からエネルギーが$U(r)$だけ必要です。少なくとも臨界半径の大きさの泡を作らないとまた萎んでしまいますので、臨界半径での泡のエネルギーを$U_0=U(2b/a)$として（これを「エネルギー障壁」と呼びます。）泡は外から$U_0$以上のエネルギーをもらわないといけないことになります。これは普通、液体の分子（ビールだと大部分は水分子）の熱運動による運動エネルギーからもらうことになります。熱運動からもらったエネルギーが$U_0$以上だった時に、始めて泡が発生するのです。しかし一旦$U_0$以上のエネルギーをもらってしまえば、あとは外からエネルギーをもらうことなしに泡は成長していくことができます。

壁の影響

残念なことに、ここまでの議論はかなり理想化されています。いままでは液体中にボコッと泡が生成する過程を考えてきました。でもビールの泡は、たいていコップの壁から発生します。しかもよく観察すると、壁のある特定の場所から発生するように見えます。それは何故かを考えてみましょう。

fiig3-4

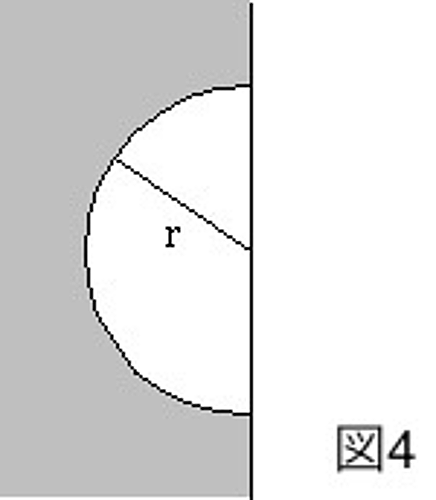
図4のように平らな壁に生じた泡を考えてみましょう。この泡を半径$r$の半球として近似することにします。すると液体と気体の界面の面積は$2πr^2$、泡の体積は$2πr^3/3$となって、それぞれ泡が球だった時の半分になります。気体と壁の界面のエネルギーは無視できるとすると、泡のエネルギー$U(r)$は、
\begin{equation} U(r) = -\frac{2\pi a}{3} r^3 + 2\pi b r^2 \end{equation}
となります。これから臨界半径を求めると、泡が球だった時と同じ$r=2b/a$となります。ところが、エネルギー障壁の大きさ$U(2b/a)$は泡が球だった時の半分になります。壁から泡が発生した方が、必要なエネルギーが半分ですむので、より泡が発生しやすくなるのです。壁の他にも、全く同様の理由によって液体中に混ざっている不純物（ホコリなど）も泡の生成をより容易にさせることが知られています。

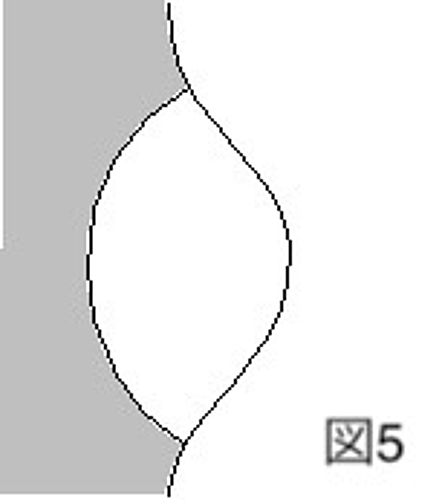fig3-5

さらに壁に凸凹があった場合も考えてみましょう。図5のように壁のへこみに発生した泡を考えてみます。すると、図4の時と比べて、同じ体積の泡に対して、気体と液体の界面の面積を小さくできることがわかります。定量的な計算をせずとも、この場合の方が界面のエネルギーを小さくできるので、泡を発生させるのに必要なエネルギーが小さくなることは明らかです。よって、泡は壁の凸凹（とくにへこんだ部分）によって、より発生しやすいことがわかります。このように泡ができる過程では、壁や不純物の影響は無視できません。こういった現象は、身の回りでも多く目にすることができます。

まず、冒頭で述べたようにビールに割箸を突っ込むと、割箸の周りから多くの泡が発生しますが、これはまさしく割箸表面の凹凸のせいであります。（コップの壁より凸凹が激しい！）また、コップの壁のある特定の場所から泡が発生するのも、その場所でコップの壁にちょっとした傷などがあるからだと、考えられます。また化学実験で突沸を防ぐために用いる沸騰石（多孔質の固体で、表面に非常に多くの凸凹がある）も、この現象を利用しています。

また、空に浮かんでいる雲は、非常に小さな水滴の集まりですが、水蒸気から水滴になる時に、空中の埃（ほこり、微小な固体）を核にしていることがわかっています。これも、ビールの泡と同様に説明できます。つまり、何もないところから水滴ができるよりも、埃などの核となるものがあったほうが、水滴を発生させるのに必要なエネルギーが少なくて済むのです。（気体と液体の立場が逆転していますが、考え方は同じです。）空中に浮かぶほこりは、一見すると汚い、あるいは無駄なもののように思われるかも知れませんが、もし空気中から埃がなくなってしまったら、空には雲一つ生じず、あの美しい虹も見ることができなくなってしまいます（虹は、光が空気中の水滴に散乱されることによってつくられます）。自然界の美しい風景に、空中の埃が一役買っているんですね。

ビールの泡と宇宙論

ビールの泡のように、ある不安定な状態（二酸化炭素が溶けている状態）から、より安定な状態（二酸化炭素が気化した状態）に移り変わる現象は、物理のさまざまな分野に普遍的に現れます。この現象を一般に一次相転移と呼んでいます。状態がいっきに移り変わらないのは、エネルギー障壁を越えるために外からエネルギーを与える必要があるからです。

一次相転移のもっとも劇的な例が一つあります。それは、ビッグバンモデル(Big bang model) です。ビッグバンという言葉は、一度は聞いたことがあるでしょう。宇宙はおよそ138億年ほど前には、非常に小さな高温、高密度の状態にあって、それがある時大爆発を起こして膨張し、現在の宇宙になっていると、多くの科学者が信じています。（宇宙は現在も膨張を続けています。）その始めの大爆発をビッグバンというわけですが、そのビッグバンがいかにして起こったか、ということはとても興味深い問題です。ビッグバンに関する理論はいろいろありますが、実は本質的な部分は泡のモデルと同じです。

ただし、大きく異なる点が一つあります。泡の発生のメカニズムを思い出してみましょう。泡が発生するには、ある一定量のエネルギーを「外」からもらってくる必要があります。ところが宇宙に対しては「外」がありません。ですから、このままでは宇宙はいつまでたっても小さいままで、ビッグバンは起こりません。これは、量子力学とよばれる理論を考えると解決できます。量子力学によれば、宇宙はエネルギー障壁を越えて、いきなり臨界半径より大きい半径の宇宙を作ることができます。先ほどの泡のモデルでいうと、半径$r=0$から、同じエネルギーを持つ半径$r=3b/a$へといきなりジャンプすることが確率的に可能なのです。（図6）この現象は、量子トンネル効果と呼びます。

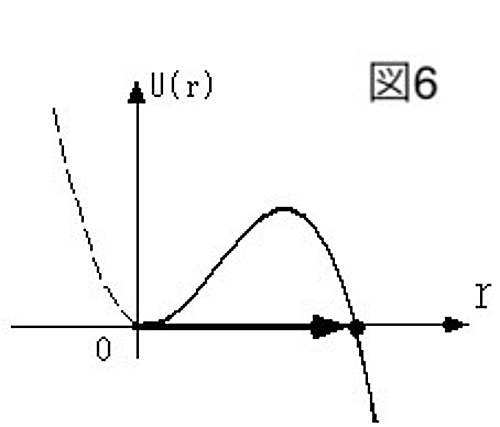fig3-6

実際のビックバンを取り扱うには、ここで説明した簡単な模型ではなく、もっときちんとした理論で取り扱う必要があります。ですが、最初のきっかけとなるのは量子トンネル効果であることはおそらく正しいと考えられています。一方、面白いことに、物性の分野でも量子核形成は観測可能です。十分冷やした低温のヘリウム4や超伝導体では、量子トンネル効果による核形成現象が観測可能です（私の博士論文のテーマの一つでした。）。そこではインスタントンと呼ばれる理論の手法が用いられますが、これは素粒子物理で用いられるものと全く同じものです。物性と素粒子で同じような現象が現れるのは、なんとも興味深いですね。