全域木の個数に関するキルヒホフの法則
全域木とは連結グラフの部分グラフですべての頂点を共有するものをいう。グラフによってはきれいに求めることができる。それについていくつかの結果を述べたい。
連結グラフ$G$に対し、その全域木の個数を$|G|$と書くことにする。
定義いろいろ
連結グラフ$G$は$2$つ以上の頂点をもつとする。$G$の異なる$2$点$p,q$に対し、この$2$点を付随させて考えたものを抵抗器と呼び$A=(G,~p,~q)$みたいに書く。なぜ$2$点を取り出して考えるのかは後でわかる。
抵抗器$A=(G,~p,~q)$の値$val(A)=(\alpha,~\beta)$とは、$G$の全域木の個数$\alpha=|G|$と、$G$の全域部分グラフで$p$を含む木と$q$を含む木の互いに頂点を共有しない合併になっているものの個数$\beta$の組とする。$\beta$はまた、$G$において$p$と$q$を同一視して得られるグラフの全域木の個数に等しい。
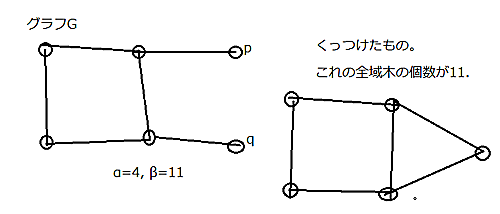抵抗器の例
抵抗器$A=(G,~p,~q)$について$p$と$q$を入れ替えたものを$A'=(G,~q,~p)$と書く。当然のごとく、$val(A)=val(A')$である。
抵抗器$A_1=(G_1,~p_1,~q_1),~A_2=(G_2,~p_2,~q_2)$について、それらの直列というのは、$q_1$と$p_2$を同一視してできる連結グラフを$G$と書くときの$A=(G,~p_1,~q_2)$のことをいう。$A=A_1\perp A_2$のように書く。結合律：
$$(A_1\perp A_2)\perp A_3=A_1\perp (A_2\perp A_3)$$
が成り立つし、逆について、
$$(A_1\perp A_2)'=A_2'\perp A_1'$$
も明らか。
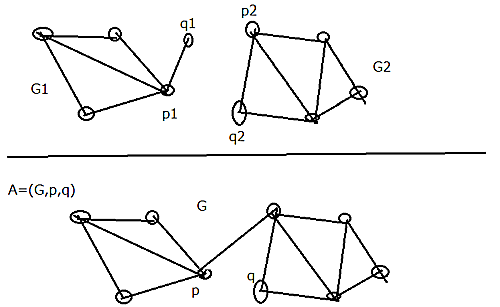直列の例
$A_1=(G_1,~p_1,~q_1),~A_2=(G_2,~p_2,~q_2)$について、それらの値を
$$val(A_1)=(\alpha_1,~\beta_1),~~~~val(A_2)=(\alpha_2,~\beta_2)$$
とするとき、直列について、
$$val(A_1\perp A_2)=(\alpha_1\alpha_2,~\alpha_1\beta_2+\beta_1\alpha_2).$$
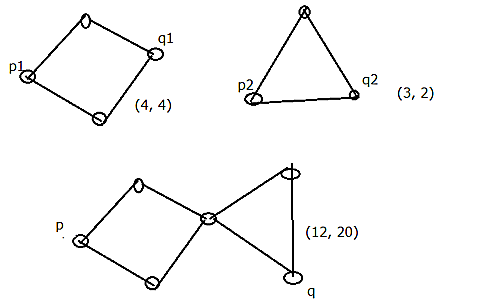直列の値
抵抗器$A_1=(G_1,~p_1,~q_1),~A_2=(G_2,~p_2,~q_2)$について、それらの並列というのは、$p_1$と$p_2$を同一視し、$q_1$と$q_2$を同一視してできる連結グラフを$G$とするときの$A=(G,~p1=p2,~q1=q2)$のことをいう。$A=A_1\parallel A_2$のように書く。次は容易に知られる：
$$(A_1\parallel A_2)\parallel A_3 = A_1\parallel (A_2\parallel A_3).$$
$$(A_1\parallel A_2)' = A_1'\parallel A_2'.$$
$$A_1\parallel A_2 = A_2\parallel A_1.$$
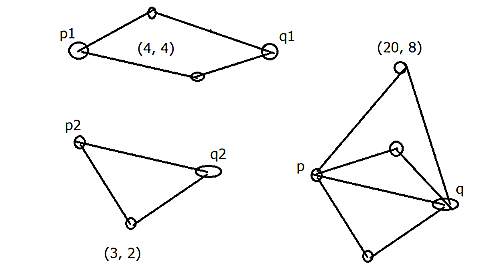
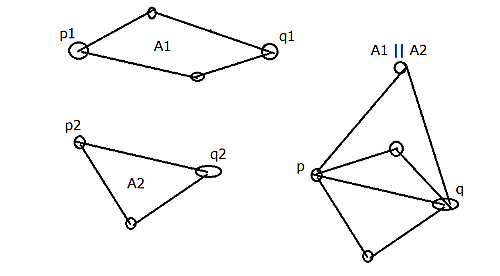並列の例
$A_1=(G_1,~p_1,~q_1),~A_2=(G_2,~p_2,~q_2)$について、それらの値を
$$val(A_1)=(\alpha_1,~\beta_1),~~~~val(A_2)=(\alpha_2,~\beta_2)$$
とするとき、並列について、
$$val(A_1\parallel A_2)=(\alpha_1\beta_2+\beta_1\alpha_2,~\beta_1\beta_2).$$
並列の値
抵抗器$A_i=(G_i,~p_i,~q_i)~(i=1,2,\cdots,n)$があるとき、$q1$と$p2$,$q2$と$p3$,$\cdots$,$q_{n-1}$と$p_n$,$q_n$と$p_1$という風に輪を作るようにしてつないでできる連結グラフを$$G=link(A_1,~A_2,~\cdots,~A_n)$$と書く。
抵抗器$A_i=(G_i,~p_i,~q_i)~(i=1,2,\cdots,n)$があるとき、それらの値を
$$val(A_i)=(\alpha_i,~\beta_i)$$
として、リンクの全域木の個数は、
$$|link(A_1,~A_2,~\cdots,~A_n)| = \alpha_1\cdots \alpha_n \left(\frac{\beta_1}{\alpha_1} + \cdots + \frac{\beta_n}{\alpha_n}\right)$$
で与えられる。特に、リンクを作るときの$A_i$たちの順序を入れ替えたり、構成する抵抗器の一部を逆で取り替えたりしても、出来上がるリンクの全域木の個数は変化しない。
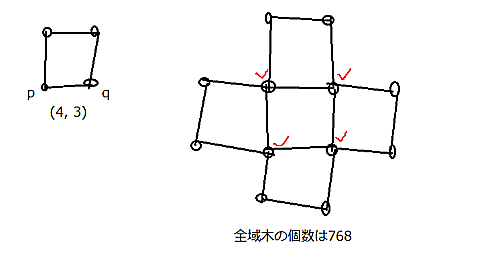
以下のリンクでは$4$つの$(4, 3)$を組み合わせているので、
$$4\cdot 4\cdot 4\cdot 4 \cdot \left( \frac{3}{4}\times 4 \right) = 768$$
が求める全域木の個数になる。
g7f6dftg
次がある意味で主定理になる。
抵抗器$A=(G,~p,~q)$を取る。$G$のすべての辺を$1\Omega$の抵抗とみなし、$p$を入力、$q$を出力として電流を流すことを考える。すなわち各辺を重み付きの矢印とし、$p$と$q$以外のすべての点で流出量の総和が等しくなるよう、また任意のサイクルで矢印に沿った重みの和（逆方向の場合はマイナス）が$0$になるようにこれを用意するとき、$p$及び$q$での流出量の絶対値$I$（電流の入力の値に当たる感じ）と$p$から$q$へ辺に沿って重みを足した和の値（逆方向の場合はマイナス）の絶対値$V$（こちらは電圧に当たる、すべての抵抗は$1\Omega$）、及び$A$の値$val(A)=(\alpha,~\beta)$について、
$$\frac{V}{I} = \frac{\beta}{\alpha}$$
が成立する。なお、$V$と$I$の比は一意的に決まる。特に、
$$\beta=\alpha\times \frac{V}{I}$$
であるから、$\alpha,~I,~V$から$\beta$を計算することができる。
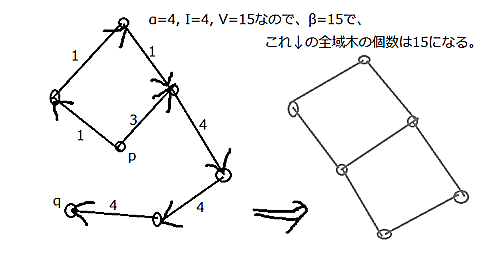
例を出した方が分かりやすい。
キルヒホフ～
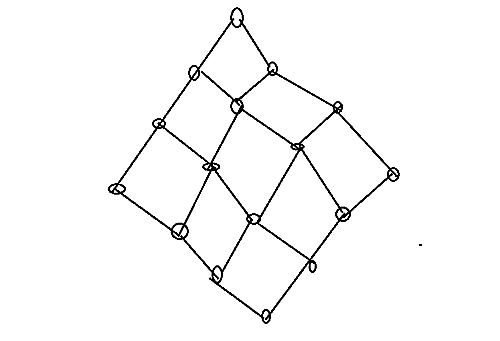
これらを使って次のグラフの全域木の個数を求めてみる。
格子
いわゆる格子である。これの実際の値は、サイクル行列定理を使えば即座に出せるが、抵抗器の考え方で地道に迫ることでその裏付けがしたい。
ステップ１
ステップ1
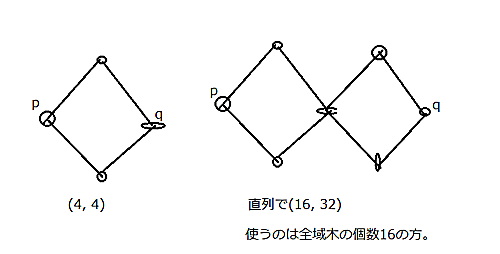
普通の正方形型グラフを用意する。全域木の個数は$4.~$図のように$p,q$を設定すると値は$(4,~4)$となり、直列して$(16,~32)$を得る。
ステップ2
ステップ2
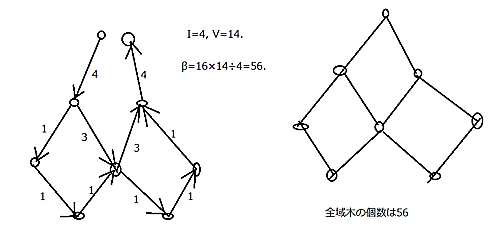
単純に辺をつけ足しても全域木の個数は変わらないので（自明）、左のグラフもまた全域木の個数は$16$である。これを回路にする。電流が$4$で電圧が$14$みたいになるので、繋げた場合の全域木の個数は、
$$16\cdot \frac{14}{4} = 56.$$
こうしてまず右のグラフの全域木の個数$56$を得る。
ステップ3
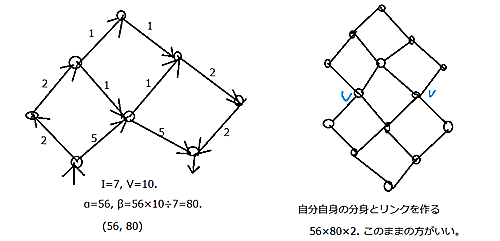
こうしてできた連結グラフの2点を左の図のように取り、値で$\beta$の方を法則に従って出すと$80$になる。抵抗器の値が$(56,~80)$になるので、リンクを作ると右のグラフの全域木の個数が$56\cdot 80\cdot 2$になる。これはそのままの方がいい。
g6t65fr56
ステップ4
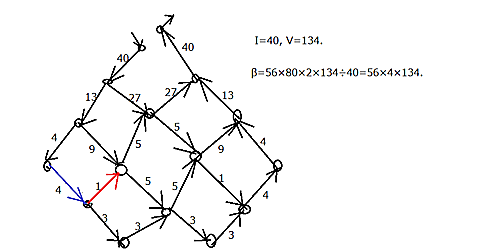
やはり辺をつけ足しても全域木の個数は変わらないので（片方の点が孤立していればOK）、左のようにすると$α$がさっき求めた$56\cdot 80\cdot 2$になる。で、抵抗計算・・図で青の所に$1$をおき、赤の所を文字でおき、法則を満たすように数を埋めていくと最後に1次方程式を解いて赤の所が$1/4$になる。だからこんな風になる。そして$\beta$の計算も、
$$56\cdot 80\cdot 2 \cdot \frac{134}{40} = 56\cdot 4\cdot 134.$$
r4t43t
ステップ5（終了）
次の回路の抵抗を計算する。
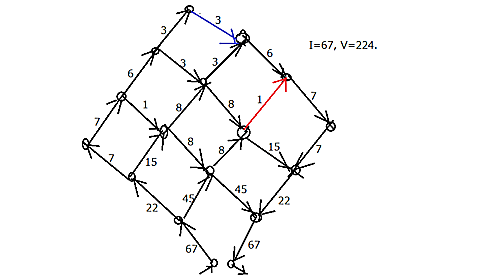fg54y546y
青い矢印を$1$と置いたうえで赤い矢印を文字でおくとそれが$1/3$と出るのでそれで分かる感じ。そこまで難しくない。$α$の方はさっき出した$56\cdot 4 \cdot 134$であるから、つないだものについては次のようになる：
$$56\cdot 4 \cdot 134 \cdot \frac{224}{67} = 56\cdot 8\cdot 224 = 100352.$$
ゆえに、求める全域木の個数は100352個である。
サイクル行列による求め方（検算）
$I$は$3$次単位行列、$O$は$3$次ゼロ行列とする。平面グラフのサイクル行列定理とは、各サイクルを添え字とし、対角成分にサイクルを構成する辺の数をプラスで、非対角成分にサイクル同士の共有辺の個数をマイナスでかいたものである。これの行列式が全域木の個数を与える。問題のグラフの場合、
$$d=\csqdet{A}{-I}{O}{-I}{A}{-I}{O}{-I}{A}.~~~ただし、~~A=\csqdet{4}{-1}{0}{-1}{4}{-1}{0}{-1}{4}$$
で与えられる$d$を計算すればいい。
$$\begin{align*}
d&=|A^3-2A| = |A| |A-\sqrt{2}I| |A+\sqrt{2}I|\\[5pt]
&=4\cdot (4-\sqrt{2})(4+\sqrt{2})(4-\sqrt{2})(4-2\sqrt{2})\cdot 4\cdot 4\cdot(4+\sqrt{2})(4+2\sqrt{2})\\[5pt]
&=4^3\cdot (4^2-2)^2\cdot (4^2-8) \\[5pt]
&=64\cdot {14}^2\cdot 8 \\[5pt]
&=100352.
\end{align*}$$
同じ値になった。
おわりに
自分で見つけたので参考文献とかはないです。シュプリンガーさんのグラフ理論かなんかの本でそれっぽい紹介があったかもしれないです。全域木の個数が分かるだけだし適用も小さいものに限られる地味な定理なので注目度は低いと思います。キルヒホフの証明は有限版のラプラシアンとか定義してやったような気がするんですけど忘れました。
直列と並列について。抵抗器の値から$β/α$として比を作ると、合成した場合の値が抵抗の値の直列並列での計算結果に一致しているのは興味深いです。
$$\frac{\beta}{\alpha} = \frac{\beta_1}{\alpha_1}+\frac{\beta_2}{\alpha_2}.~~(直列)~~~~~~~~\frac{\alpha}{\beta} = \frac{\alpha_1}{\beta_1}+\frac{\alpha_2}{\beta_2}.~~(並列)$$