JMO2020予選感想

とてつもなくお久しぶりです。PCTです。
今日はJMO2020の予選を解いてみたので感想を書いていきます。コメントは付けますが解説はあまりしません。あしからず。

面倒枠。$A0B$+$2020$ に分けてあげてそれぞれの $\bmod 7$ を計算してあげる。

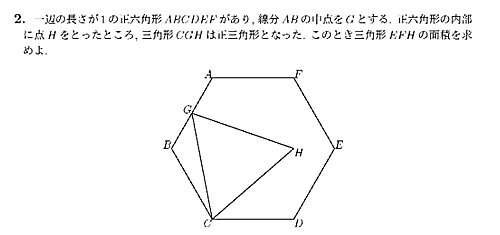
なんか時間かかった。$B,C,H,G$ が共円なのに気付いて計算パーティー

明らかに $6$ が怪しい。$6$ は角にしか来ないかつ隣には $1,5$ しか入らないので後は $2$ と $4$ が隣り合わないようにしてあげればいい。

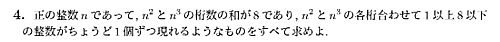
これも明らかに面倒枠。始めの条件で $n$ の範囲が $9$ 個くらいに絞れるのでそこから $1$ の位を見て $2$ 個くらいの候補になるので後は両方計算してあげれば終わり。

それぞれの項は正整数でなくてもいいことに注意。とりあえず全て絶対値が $0$ 以外の最小値を取るようにすると計算結果が負になってしまうので $2$ 個目に絶対値が最小値となるものの内始めとの倍率が一番小さいものを選ぶ。
誤読に注意。(やらかしかけた)

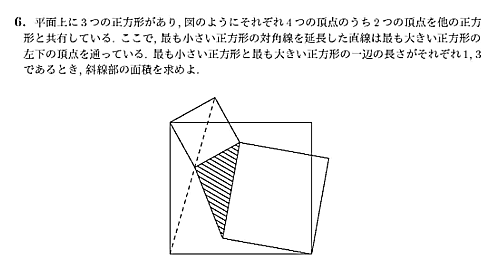
解けなかった。(は？)
色々パラメーターをおいてガチャガチャしてたらよくわからなくなってしまった。
真ん中の正方形と一番大きい正方形のそれぞれの左下の頂点を結んであげたら平行と合同が見える。凄い。

試せばわかるの典型例。始めの $2$ 個を決めるとその後の $2$ 個は必ず $3$ 通りしか候補がないことが分かります。$1010$ という比較的大きめな数字の存在からして試したくなる気持ちがありますね。

条件が結構複雑。$(i)$ は狭義単調増加数列ということですが $(ii)$ をどう生かすか。
とりあえず $(ii)$ に関係しない $a_1$ から $a_5$ を $1,2,3,4,5$ にして試すと $a_6=a_3×2$ とするしかないです。ここで少し怪しいのが $a_1$ をここで選ぶことが出来たら指数爆発を少しは抑えられるのでは？ということです。試しに $a_1$ から $a_5$ を $5,6,7,8,9$ にしてあげるとこの場合が最適解ということが分かるので後はこれの $a_{100}$ を求めればいいです。始めで違和感を感じないとそのまま間違えてしまいそうな問題。

とりあえず関数の条件からして $m^{f(n)}$ という形で表せるものは全て $2^2=4$ 以上であることが分かります。
次に $f(n)≠3$ としてみると、$f(6^3)=2$ と定義できます。この時に $f(2)=2$ と一緒に定義することにより $f(6^6)=2^2=4$ となり、理論値を取ります。
議論が結構曖昧ですがコメントなのでご愛敬...

上から奇数行目に白黒をそれぞれ $2$ 個ずつ、偶数行目にも同様にすればいいので後はこれをカウントすればいいです。

なにこれ。何もわからない。

運ゲーかな？適当にガチャガチャ構築してたらなんとなく長い解が出来るのでそれを信じてやると、うまく行きます。

これで終わりです。$6,11$ 落としの $10$ 完でした。幾何が少な目の得意回だったのでボーダーぴったりだと逆に怖いので安心です。
何か詳しく書いてほしい問題があったら教えてください。では。