正多角形の頂点の入れ替え方は何通り?
はじめに
こんにちはQooです.大学で数学を学んでいます.
今回は1年ほど前に数学とは直接関係の無い内容のTwitterスペースで話題に挙がっていた問題を解いてみたら面白かったので,それについて書きたいと思います.
記事のレベルとしては群の準同型定理ぐらいまで知っている人を想定して書きました(上に書いたような経緯からできるだけ前提知識なしで読めるようにしたかったため).
群の作用が出てきますが,この記事で使う事柄は
群の作用について
のところにまとめてあります(ほとんどが定義です).
なるべく多くの人が読める記事にするために丁寧な記述を心がけました.
間違いなど見つけたら優しく教えてもらえると有難いです.
この記事で考えたい問題
この記事では次の問題を解きたいと思います.
$n$を正の整数とする.正$n$角形($n=1$の時は1点,$n=2$の時は線分とする)が一つ与えられ,その頂点を以下の条件を満たすように向き付きの辺で結ぶ.
(条件) 正$n$角形の各頂点$v$について$\deg_{\mathrm{in}}(v)=\deg_{\mathrm{out}}(v)=1$.
このとき条件を満たすような図形は何通りあるか?ただし回転によって重なるものは同一視する.
ここで$\deg_{\mathrm{in}}(v)$は頂点$v$を始点とする辺の個数,$\deg_{\mathrm{out}}(v)$は頂点$v$を終点とする辺の個数を表します.
この問題ではループ(始点と終点が同じである辺)を許しています.
この記事の目標は以下の式を示すことです.
mondaiの状況で条件を満たすような図形の総数を$E_n$とすると$E_n$は次の式で表される.
\begin{align*}
E_n = \sum_{d|n} {\varphi\!\left(\frac{n}{d}\right)\left(\frac{n}{d}\right)^{d-1}\!(d-1)!}
\end{align*}
ただし$\varphi$はオイラーのトーシェント関数.
例
ここではmondaiで考える図形についてのいくつかの例を挙げておきます.
条件を満たす図形の例
$n=5とn=6$のときの例を以下に示します.
![!FORMULA[16][36584066][0]の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FUq4GWZuj4USEVBFLlBaK.png?alt=media) $n=5$の例
$n=5$の例
![!FORMULA[17][36584097][0]の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FC1O17R3Uaj97oytyIEjf.png?alt=media) $n=6$の例
$n=6$の例
条件を満たさない図形の例
次に示す図形はどれも条件を満たしません.
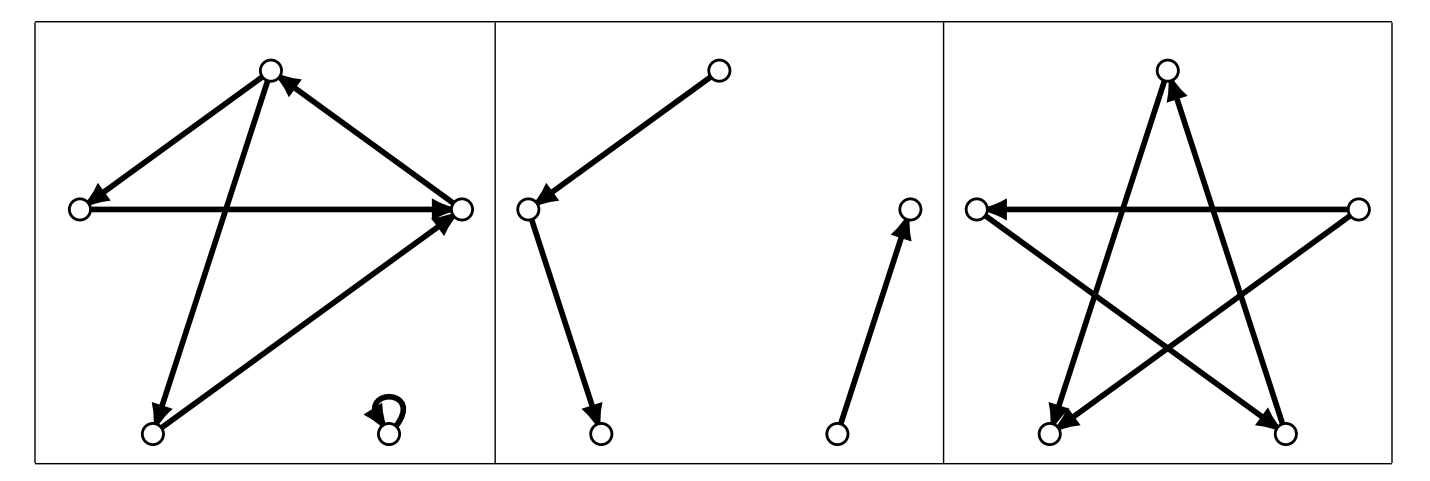 条件を満たさない例
条件を満たさない例
回転によって重なる図形の例
次に示す図形は横に並んでいるものは回転によって重なるので同一視します.
 回転で重なる例
回転で重なる例
回転で重ならない図形の例
次に示す図形はどの二つも回転で重ならないので同一視されません.
 回転で重ならない例
回転で重ならない例
mondaiの条件を満たす図形一つに対して辺の向きを無くしたときに同じ形になる図形がいくつあるかはその図形が含む頂点数3以上のサイクルの数やその図形の対称性によって変わります.例えば上の例だと辺の向きがある図形と辺の向きを無くした図形が3対1に対応していますが,2つのサイクルから成る図形で"対称性の低いもの"は4対1に対応します.
準備とこの記事で使う記号
mondaiを解くための準備としてこの記事で使う範囲の事柄をまとめておきます.知っている人は適宜読み飛ばしてください.
記号のまとめ
- $\mathbb{N}$で正の整数全体の集合を,$\mathbb{Z}$で整数全体の集合を表します.
- 正の整数$n$に対して$\mathfrak{S}_n$で$n$次対称群を表します.
- 特に断らなければ$\mathfrak{S}_n$は$\mathbb{Z}/n\mathbb{Z}$上の全単射全体の成す群とみなし,同値類$i+n\mathbb{Z}$を単に$i$と書きます.
- 群$G$に対して$\Aut G$で$G$の自己同型全体の成す群を,$\Int G$で$G$の内部自己同型全体の成す群を表します.
- 集合$X$に対して$X$上の全単射全体の成す群を$S(X)$と書きます.
- 全体集合$X$とその部分集合$A\subset X$に対して$A^{c}\coloneqq X\setminus A$と書きます.
- $\varphi : \mathbb{N}\longrightarrow\mathbb{N}$をオイラーのトーシェント関数とします.つまり,任意の正の整数$n$に対して$\varphi (n)$で$n$と互いに素である$n$以下の正の整数の個数を表します.
- 数列$a_1,...,a_n\in\mathbb{Z}$に対して$\sum_{d|n}a_d$は$d$を$n$の正の約数すべてについて渡って和を取ることを表します.
- 例えば$\sum_{d|6}a_d=a_1+a_2+a_3+a_6$,$\sum_{d|7}a_d=a_1+a_7$です.
- $\bigsqcup_{d|n} $についても同様です.
次の定理は参照できると便利なのでここで紹介しておきます.
$X,Y$を集合とし,全射$f:X\to Y$が与えられているとする.このとき$X$上の二項関係を
\begin{align*}
x\sim_fy\xLeftrightarrow{\mathrm{def}}f(x)=f(y)
\end{align*}
によって定めると$\sim_f$は同値関係であり,$i:X\to X/{\sim_f}$を自然な全射とすれば$f=\tilde{f}\circ i$を満たす全単射$\tilde{f}:X/{\sim_f}\to Y$がただ一つ存在する.
$X/{\sim_f}$は各$y\in Y$の一点の逆像$f^{-1}(\{y\})$を集めた集合です.こう考えるとsyousyazouは当たり前に思えるかもしれません.
$\sim_f$が同値関係であることは省略.
まず$f=\tilde{f}\circ i$を満たす$\tilde{f}$が一意に存在することを示します.$x\in X$に対して$i(x)=[x]$と書きます.このとき$\tilde{f}$としてありうるのは
$$
\tilde{f}:X/{\sim_f}\ni[x]\longmapsto f(x)\in Y
$$
のみです.これが well-defined であることを見ればよいです.
$[x]=[y]$とすると定義から$f(x)=f(y)$なので上の$\tilde{f}$は well-defined です.
$\tilde{f}$は作り方から明らかに$f=\tilde{f}\circ i$を満たし,さらに$f$は全射なので$\tilde{f}$も全射です.
次に単射性を示します.$\tilde{f}([x])=\tilde{f}([y])$とすると$f(x)=f(y)$なので$\sim_f$の定義から$x\sim_f y$,つまり$[x]=[y]$です.
オイラーのトーシェント関数の性質
ここではオイラーのトーシェント関数についてこの記事で使う性質をまとめておきます.
まず次の式を示します.
$n\in\mathbb{N}$が$n=p_1^{e_1}\cdots p_r^{e_r}\;$($p_1,...,p_r$は相異なる素因数$,e_1,...,e_r\in\mathbb{N}$) と素因数分解されているとすると
\begin{align*}
\varphi(n) = n\prod_{i=1}^{r}{\left(1-\frac{1}{p_i}\right)}
\end{align*}
包除原理を使います.
$n$と互いに素$\Leftrightarrow$$\{p_1$の倍数でない$\}\cap\cdots\cap\{ p_r$の倍数でない$\}$
に注意します.$A_{p_i}=\{k\in\{1,...,n\}\mid k\text{は$p_i$の倍数} \}$とすると
\begin{align*}
\varphi(n) &= |A_{p_1}^{c}\cap\cdots\cap A_{p_r}^{c}|\\
&=n-|A_{p_1}\cup\cdots\cup A_{p_r}|\\
&=n+\sum_{\substack{1\leq i_1 <\cdots< i_k\leq r\\1\leq k\leq r}}(-1)^{k}|A_{p_{i_1}}\cap\cdots\cap A_{p_{i_k}}|\\
&=n+\sum_{\substack{1\leq i_1 <\cdots< i_k\leq r\\1\leq k\leq r}}\frac{(-1)^k n}{p_{i_1}\cdots p_{i_k}}\\
&= n\prod_{i=1}^{r}{\left(1-\frac{1}{p_i}\right)}
\end{align*}
2行目の等号はド・モルガンの法則から,4行目の等号は$p_1,...,p_r$が相異なる素数であることから従います.
互いに素な正の整数$n,m\in\mathbb{N}$について次が成り立つ.
\begin{align*}
\varphi(nm)=\varphi(n)\varphi(m)
\end{align*}
このような性質を持つ自然数からの0でない関数を乗法的関数と呼びます.
$n,m$がそれぞれ$n=p_1^{e_1}\cdots p_r^{e_r},\;
m=q_1^{f_1}\cdots q_s^{f_s}$と素因数分解されているとします.$n$と$m$は互いに素なので$p_1,...,p_r,q_1,...,q_s$は互いに異なる素数であり$nm$は$nm=p_1^{e_1}\cdots p_r^{e_r}q_1^{f_1}\cdots q_s^{f_s}$と素因数分解されます.よってphikousikiより
\begin{align*}
\varphi(n)\varphi(m)
&=\left(n\prod_{i=1}^{r}\left(1-\frac{1}{p_i}\right)\right)\left(m\prod_{j=1}^{s}\left(1-\frac{1}{q_j}\right)\right)\\
&=nm\prod_{i=1}^{r}\left(1-\frac{1}{p_i}\right)\prod_{j=1}^{s}\left(1-\frac{1}{q_i}\right)\\
&=\varphi(nm)
\end{align*}
最後に次の性質を示します.
任意の$n\in\mathbb{N}$に対して次の式が成り立つ.
\begin{align*}
n=\sum_{d|n}\varphi(d)
\end{align*}
まず$n$が素数冪の場合,つまり素数$p$と非負整数$m$があって$n=p^{m}$と書ける場合について証明します.このとき
\begin{align*}
\sum_{d|n}\varphi(d)&=\sum_{k=0}^{m}\varphi(p^{k})
=1+\sum_{k=1}^{m}{(p^k-p^{k-1})}\\
&=1+p^m-p^0=p^m=n
\end{align*}
よりphinowaは成り立ちます.
次に$s_{\varphi}(n)\coloneqq\sum_{d|n}\varphi(d)$とおいて$s_{\varphi}$が乗法的であることを示します.これが示されれば,素数冪の場合の結果からphinowaがわかります.$n,m$を互いに素な自然数とします.phihazyouhoutekiより
\begin{align*}
s_{\varphi}(n)s_{\varphi}(m)
&=\left(\sum_{d|n}\varphi(d)\right)\left(\sum_{l|m}\varphi(l)\right)
=\sum_{d|n}\sum_{l|m}\varphi(dl)
\end{align*}
です.$d,l$の取り方から$dl|nm$です.逆に$t$を$nm$の正の約数とすると$t$が$n$の正の約数と$m$の正の約数の積として一意的に書けることを示しましょう.
$d=\gcd(t,n),l=\frac{t}{d}$とします.定め方から$t=dl$であり,$d$は$t$の正の約数なので$l$は自然数です.定め方から$d$は$n$の約数であり,$\frac{t}{l}=d$と$t$が$nm$の約数であることから$l$は$nm$の約数であり,さらに$d$は$n$と$t$の最大公約数であることから$n$と$l\ (=\frac{t}{d})$は互いに素なので$l$は$m$の約数になります.
$n$の正の約数$d'$と$m$の正の約数$l'$があって$dl=d'l'$と書けたと仮定します.$d$と$l'$,$d'$と$l$は互いに素なので$d'$は$d$の倍数であり,逆に$d$は$d'$の倍数であるので$d=d'$がわかり,これから直ちに$l=l'$も従います.
従って$n$と$m$が互いに素なら
\begin{align*}
s_{\varphi}(n)s_{\varphi}(m)
=\sum_{d|n}\sum_{l|m}\varphi(dl)
= \sum_{t|nm}\varphi(t)
=s_{\varphi}(nm)
\end{align*}
となり$s_{\varphi}$は乗法的関数です.以上よりphinowaが示されました.
ちなみに,メビウス関数$\mu$を知っていればphikousikiの右辺を展開すると
\begin{align*}
\varphi(n)
&=\sum_{d|n}\mu(d)\frac{n}{d}
\end{align*}
であることがわかるので,メビウスの反転公式からphinowaの式が成立することがわかります.
群の作用について
群の作用についてこの記事で使う範囲の事柄をまとめておきます.
群$G$と集合$X$について,写像
\begin{align*}
G\times X \to X && ((g,x)\mapsto gx)
\end{align*}
が与えられて,次の二つの条件を満たすとき,群$G$は集合$X$に(左から)作用するという.
- \begin{align*} (gh)x=g(hx) && (g,h\in G , x\in X) \end{align*}
- \begin{align*} ex=x && (x\in X, e\text{は$G$の単位元}) \end{align*}
このとき,$G$を$X$の変換群,$X$を$G$集合(または$G$空間)という.
群$G$の集合$X$への作用を考えることは,$G$から集合$X$上の全単射全体から成る群$S(X)$への準同型を一つ与えることと同等です.
群の作用が与えられるとその作用について以下のように軌道や商が定義されます.
群$G$が集合$X$に作用しているとき,$x\in X$に対して
\begin{align*}
O_G(x)=Gx\coloneqq \{gx\mid g\in G\}
\end{align*}
を$x$の$G$軌道という.$O_G(x)$を単に$O(x)$とも書く.
群$G$が集合$X$に作用しているとする.このとき$X$上の二項関係を
$$ x\sim_G y \xLeftrightarrow[]{\rm{def}} x\in O_G(y)$$
によって定めると$\sim_G$は$X$上の同値関係を定める.
同値関係$\sim_G$による商集合$X/{\sim_G}$を単に$G\backslash X$と書き,$G$集合$X$の$G$による商という.
要するに$G\backslash X$は軌道全体から成る集合です.
群$G$が集合$X$に作用しているとき,$x\in X$に対して
$$\Stab(x)\coloneqq\{g\in G \mid gx=x\}$$
を$x$の固定化部分群という.
この記事では$G$の部分群$H$に対して
$$\Stab^{-1}(H)\coloneqq\{x\in X\mid \Stab(x)=H\}$$
と約束します.
$\Stab(x)$は$G$の部分群になります.実際$ex=x$より$e\in\Stab(x)$であり,$g\in\Stab(x)$なら$g^{-1}x=g^{-1}(gx)=(g^{-1}g)x=ex=x$より$g^{-1}\in\Stab(x).g,h\in\Stab(x)$なら$(gh)x=g(hx)=gx=x$より$gh\in\Stab(x)$です.
群$G$が集合$X$に作用しているとする.$G$の任意の部分群$H$に対して
$$X^H\coloneqq\{x\in X \mid \forall h\in H,hx=x\}$$
を$X$の$H$-不変部分集合と呼ぶ.
特に$X$が群で,群$G$の集合$X$への作用が準同型$G\to\Aut X$ によって与えられるとき,$G$の任意の部分群$H$に対して$H$-不変部分集合$X^H$は$X$の部分群になります.
実際,$e_X$を$X$の単位元とすると任意の$h\in H$に対して$h e_X=e_X$となる$(\because h\in \Aut X)$ので$X^H$は空集合ではありません.さらに$x,y\in X^H$とすると任意の$h\in H$に対して$h(xy^{-1})=(hx)(hy)^{-1}=xy^{-1}$より$xy^{-1}\in X^H$であるので$X^H$は$X$の部分群になります.
群$G$が集合$X$に作用しているとする.$x\in X$について全単射
\begin{align*}
G/\Stab(x)\ni g\Stab(x)\longmapsto gx\in O(x)
\end{align*}
が存在する.特に$G$が有限群のときはラグランジュの定理より
\begin{align*}
|G|=|O(x)||\Stab(x)|
\end{align*}
が成り立つ.
syousyazouを写像$o:G\ni g\mapsto gx\in O(x)$に適用すればよいです.
実際この写像は軌道の定義より全射で,$g,h\in G$について,
\begin{align*}
gx=hx
\Leftrightarrow x=g^{-1}hx
\Leftrightarrow g^{-1}h\in\Stab(x)
\Leftrightarrow h\in g \Stab(x)
\end{align*}
なのでsyousyazouの書き方で
\begin{align*}
G/{\sim_{o}}=G/\Stab(x)
\end{align*}
であり$\tilde{o}$はstaborbitのものになります.
本編
問題の言いかえ
mondaiを群の作用の言葉で言いかえていきます.
正$n$角形の頂点に$v_1,...,v_n$とこの順に反時計回りに並ぶように名前を付けておきます.mondaiの条件を満たす辺のおき方を考えると,任意の$i \; (1\leq i \leq n)$に対して$v_i$を始点とする辺と終点とする辺が一つずつ存在するので,各辺の始点に対して終点を対応させることにより$S(\{v_1,...,v_n\})\cong\mathfrak{S}_n$の元が一つ定まります.
逆に$\sigma\in\mathfrak{S}_n$に対して$v_i$を始点として$v_{\sigma(i)}$を終点とする辺を全て置くことで条件を満たす図形が一つ定まります.
これらの対応は互いに逆の対応になっているので,以降この対応によってmondaiの条件を満たす図形全体(回転によって重なるものを同一視しない)と$\mathfrak{S}_n$を同一視します.
この同一視の下,回転によって重なることは以下のように書くことができます.
上の状況で$\sigma,\tau\in\mathfrak{S}_n$に対応する図形が回転によって重なることは次と同値
\begin{align*}
\exists k\in\mathbb{Z}/n\mathbb{Z}, \sigma(i)-k=\tau(i-k) && (\forall i \in \mathbb{Z}/n\mathbb{Z})
\end{align*}
これは$\mathfrak{S}_n\ni\alpha\coloneqq(1\;2\; ...n):i\mapsto i+1$とすると
\begin{align*}
\exists k\in\mathbb{Z}, \sigma=\alpha^k\tau\alpha^{-k}
\end{align*}
と言いかえることができます.
$v_{i+n} = v_i$を満たすように頂点の添え字を整数の範囲まで広げておきます.
$\sigma$が表す図形で頂点$v_i$から出た辺は頂点$v_{\sigma(i)}$に入ります.この図形を$-\frac{2\pi k}{n}$だけ回転させて重なる図形が$\tau$で表されるとすると頂点$v_{i-k}$から出た辺は$v_{\sigma(i)-k}$に入ることになります.
これが$\sigma=\alpha^k\tau\alpha^{-k}$で書けることはは各元の行先を見ればわかります.
kaiteniikaeを踏まえるとmondaiは次のように言いかえられます.
$n$次巡回群$\mathbb{Z}/n\mathbb{Z}$の$n$次対称群$\mathfrak{S}_n$への作用$\rho:\mathbb{Z}/n\mathbb{Z}\to\Int\mathfrak{S}_n$を次のように定める.
\begin{align*}
\rho(k+n\mathbb{Z}):\mathfrak{S}_n\ni\sigma\mapsto\alpha^k\sigma\alpha^{-k}\in\mathfrak{S}_n
\end{align*}
この作用による軌道の個数$E_n\; (=|(\mathbb{Z}/n\mathbb{Z})\backslash\mathfrak{S}_n|)$はいくつか?
$\alpha$の位数が$n$であることからmondaiiikaeの$\rho$は well-defined なことがわかります.
kotaeの証明
まず次の補題を示します.
$E_n$は次の式で書ける.
\begin{align*}
E_n = \frac{1}{n}\sum_{d|n}\varphi\!\left(\frac{n}{d}\right)|\mathfrak{S}_n^{\langle d \rangle}|
\end{align*}
有限巡回群が有限集合に作用していればこれと同様の式が成り立ちます.
巡回群$\mathbb{Z}/n\mathbb{Z}$の部分群は$n$の正の約数$d$を用いて$\langle d\rangle$と書けるもので尽くされます.よって
\begin{align*}
\mathfrak{S}_n = \bigsqcup_{d|n}\Stab^{-1}(\langle d \rangle)
\end{align*}
であり,staborbitより$\sigma\in\Stab^{-1}(\langle d \rangle)$なら
\begin{align*}
|O(\sigma)| &= \frac{|\mathbb{Z}/n\mathbb{Z}|}{|\Stab(\sigma)|} = \frac{|\mathbb{Z}/n\mathbb{Z}|}{|\langle d \rangle|}
= \cfrac{n}{\left(\cfrac{n}{d}\right)} = d
\end{align*}
なので
\begin{align*}
E_n=|(\mathbb{Z}/n\mathbb{Z})\backslash\mathfrak{S}_n|=\sum_{d|n}{\frac{1}{d}|\Stab^{-1}(\langle d \rangle)|}
\end{align*}
また定義より任意の$\mathbb{Z}/n\mathbb{Z}$の部分群$\langle d \rangle$に対して次が成り立ちます.
\begin{align*}
\sigma\in\mathfrak{S}_n^{\langle d \rangle}
\Longleftrightarrow\text{
$\langle d \rangle$が$\Stab(\sigma)$の部分群}
\end{align*}
従って
\begin{align*}
\mathfrak{S}_n^{\langle d \rangle}
&= \bigsqcup_{l|d}\Stab^{-1}(\langle l \rangle)\\
\therefore |\mathfrak{S}_n^{\langle d \rangle}|
&= \sum_{l|d}|\Stab^{-1}(\langle l \rangle)|
\end{align*}
これらから次のように計算できます.
\begin{align*}
E_n &= \sum_{d|n}{\frac{1}{d}|\Stab^{-1}(\langle d \rangle)|}
=\frac{1}{n}\sum_{d|n}{\frac{n}{d}|\Stab^{-1}(\langle d \rangle)|}\\
&=\frac{1}{n}\sum_{d|n}{|\Stab^{-1}(\langle d \rangle)|}\sum_{l|\frac{n}{d}}\varphi(l)
=\frac{1}{n}\sum_{dl|n}{|\Stab^{-1}(\langle d \rangle)|}\varphi(l)\\
&=\frac{1}{n}\sum_{l|n}{\varphi(l)}\sum_{d|\frac{n}{l}}|\Stab^{-1}(\langle d \rangle)|
=\frac{1}{n}\sum_{l|n}{\varphi(l)|\mathfrak{S}_n^{\langle \frac{n}{l} \rangle}|}\\
&= \frac{1}{n}\sum_{d|n}\varphi\!\left(\frac{n}{d}\right)|\mathfrak{S}_n^{\langle d \rangle}|
\end{align*}
1行目から2行目への変形はphinowaによります.
あとは$|\mathfrak{S}_n^{\langle d \rangle}|$を計算すればkotaeの証明が完了します.
$\mathbb{Z}/n\mathbb{Z}$の$\mathfrak{S}_n$への作用が$\mathbb{Z}/n\mathbb{Z}$から$\Int\mathfrak{S}_n\subset\Aut\mathfrak{S}_n$への準同型によって与えられていることから,$n$の任意の正の約数$d$について$\mathfrak{S}_n^{\langle d \rangle}$は$\mathfrak{S}_n$の部分群になります.$d$を固定します.
$\pi:\mathbb{Z}/n\mathbb{Z}\to(\mathbb{Z}/n\mathbb{Z})/(d\mathbb{Z}/n\mathbb{Z})\cong \mathbb{Z}/d\mathbb{Z}$を自然な射影とします.
任意に$\sigma\in\mathfrak{S}_n^{\langle d \rangle}$を取ります.まず全射$\pi\circ\sigma$について
\begin{align*}
\pi\circ\sigma(i)=\pi\circ\sigma(j) &\Longleftrightarrow
\sigma(i)-\sigma(j)\in d\mathbb{Z}/n\mathbb{Z}\\
&\Longleftrightarrow i-j \in d\mathbb{Z}/n\mathbb{Z}
\end{align*}
であることを示します.一つ目の$\Leftrightarrow$は定義より明らかです.$\sigma\in\mathfrak{S}_n^{\langle d \rangle}$より
\begin{align*}
\sigma(i+d)&=\sigma(i)+d &(\forall i \in \mathbb{Z}/n\mathbb{Z})
\end{align*}
なので二つ目の$\Leftrightarrow$の$\Leftarrow$はすぐわかります.さらに$\sigma^{-1}\in\mathfrak{S}_n^{\langle d \rangle}$でもあることから$\Rightarrow$もわかります.
これとsyousyazouから以下の図式を可換にする全単射$\Phi(\sigma)\;($つまり$\pi\circ\sigma=\Phi(\sigma)\circ\pi$を満たす全単射$\Phi(\sigma) )$が一意に存在することがわかります.
\begin{xy}\xymatrix{
\mathbb{Z}/n\mathbb{Z} \ar[rr]^{\sigma} \ar[d]_{\pi} && \mathbb{Z}/n\mathbb{Z} \ar[d]^{\pi} \\
(\mathbb{Z}/n\mathbb{Z})/(d\mathbb{Z}/n\mathbb{Z}) \ar@{.>}[rr]^{\exists! \Phi(\sigma)} &&
(\mathbb{Z}/n\mathbb{Z})/(d\mathbb{Z}/n\mathbb{Z}) \ar@{}[llu]|{\large{\circlearrowright}} \\
}\end{xy}
この対応$\Phi:\mathfrak{S}_n^{\langle d \rangle}\to\mathfrak{S}_d$は定め方から群準同型です(以下の図式を参照).
\begin{xy}\xymatrix{
\mathbb{Z}/n\mathbb{Z} \ar[r]^{\sigma} \ar[d]_{\pi} & \mathbb{Z}/n\mathbb{Z} \ar[d]^{\pi} \ar[r]^{\tau} &
\mathbb{Z}/n\mathbb{Z} \ar[d]^{\pi} \\
(\mathbb{Z}/n\mathbb{Z})/(d\mathbb{Z}/n\mathbb{Z}) \ar@{.>}[r]^{\exists! \Phi(\sigma)}
\ar@{.>}@/_15pt/[rr]_{\exists! \Phi(\tau\sigma)} &
(\mathbb{Z}/n\mathbb{Z})/(d\mathbb{Z}/n\mathbb{Z})
\ar@{.>}[r]^{\exists! \Phi(\tau)}
\ar@{}[lu]|{\large{\circlearrowright}} &
(\mathbb{Z}/n\mathbb{Z})/(d\mathbb{Z}/n\mathbb{Z}) \ar@{}[lu]|{\large{\circlearrowright}} \\
}\end{xy}
また$\Psi:\mathfrak{S}_d\to\mathfrak{S}_n^{\langle d \rangle}$を
\begin{align*}
\Psi(\sigma)(i+kd) &= \sigma(i)+kd & \left(1\leq i\leq d, 0\leq k < \frac{n}{d}\right)
\end{align*}
によって定めることができて,$\Phi\circ\Psi=\mathrm{id}_{\mathfrak{S}_d}$であるので$\Phi$は全射です.
\begin{align*}
\ker\Phi &= \{\sigma\in\mathfrak{S}_n^{\langle d \rangle} \mid \sigma(i)-i\in d\mathbb{Z}/n\mathbb{Z}\;(\forall i \in\mathbb{Z}/n\mathbb{Z}) \}
\end{align*}
であり,$\mathfrak{S}_n^{\langle d \rangle}$の元は$1,...,d$の$d$個の行先を定めれば決まることに注意すると,写像
\begin{align*}
\ker\Phi\ni\sigma\longmapsto(\sigma(1)-1,...,\sigma(d)-d)\in(d\mathbb{Z}/n\mathbb{Z})^d
\end{align*}
は単射です.逆に任意の$(k_1,...,k_d)\in(d\mathbb{Z}/n\mathbb{Z})^d$に対して$\sigma(1)=1+k_1,...,\sigma(d)=d+k_d$によって$\ker\Phi$の元が一つ定まるのでこの写像は全単射であることがわかります.従って
\begin{align*}
|\ker\Phi|=\left(\frac{n}{d}\right)^{d}
\end{align*}
がわかります.準同型定理より
\begin{align*}
|\mathfrak{S}_n^{\langle d \rangle}|=|\ker\Phi||\Im\Phi|=\left(\frac{n}{d}\right)^d d!
\end{align*}
です.これとwanokakikaeより
\begin{align*}
E_n &= \frac{1}{n}\sum_{d|n}\varphi\!\left(\frac{n}{d}\right)|\mathfrak{S}_n^{\langle d \rangle}|
= \frac{1}{n}\sum_{d|n}\varphi\!\left(\frac{n}{d}\right)\left(\frac{n}{d}\right)^d d!\\
&= \sum_{d|n}\varphi\!\left(\frac{n}{d}\right)\left(\frac{n}{d}\right)^{d-1}\!(d-1)!
\end{align*}
以上よりkotaeが示されました.
この式の右辺は$d=n$の項が支配的で
\begin{align*}
%E_n>(n-1)!&& (\forall n\in\mathbb{N})\\
\lim_{n\to\infty}{\frac{E_n}{(n-1)!}} &=1
\end{align*}
がわかります.これはほとんどの図形は回転についての対称性がないという直感とも合っています.
あまりちゃんとした言い方ではないですが,同じくらいの$n$に対しては$E_n - (n-1)!$の値は$n$の約数が多いほど,$n$が小さい約数を多く持つほど大きくなります.これは,より小さい角度の回転で自身と重なるような対称性の高い図形が多いからといえます.実際に$E_n - (n-1)!$を計算すると以下のようになります.($n=18,20$での値は間違っている可能性があります.)
| $n$ | $E_n-(n-1)!$ | $n$ | $E_n-(n-1)!$ | $n$ | $E_n-(n-1)!$ | $n$ | $E_n-(n-1)!$ | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 6 | 16 | 11 | 10 | 16 | 645928 | |||
| 2 | 1 | 7 | 6 | 12 | 4244 | 17 | 16 | |||
| 3 | 2 | 8 | 60 | 13 | 12 | 18 | (10380444) | |||
| 4 | 4 | 9 | 42 | 14 | 46128 | 19 | 18 | |||
| 5 | 4 | 10 | 408 | 15 | 4096 | 20 | (185809896) |
今後の展望
mondaiを発展させた問として
- 裏返し(鏡映)によって重なる図形も同一視する
- 辺の向きを無くす
- 上二つの組み合わせ
が考えられると思います.
(1)では正二面体群$D_n$による作用を考えればこの記事と同じように商$D_n\backslash\mathfrak{S}_n$の大きさを計算することに帰着されます.この作用は$\Int\mathfrak{S}_n$への準同型で与えられます.
(2)は巡回群が作用する集合の方が変わります.まだちゃんと計算はしてないですが概ねこの記事と同じようにできると思います.ただ,作用する先の集合が群じゃないのでこの記事ほどきれいな議論にはならないと思います.
解けたらこれらについても書きたいと思います.
おわりに
群は対称性を記述しているとよく言われますが,この記事の例では$\mathbb{Z}/n\mathbb{Z}$が回転を表しているのが見て取れますね.群の作用を考えることで「回転による違いを無視する」というのを代数の言葉で表すことができました.
この記事で扱った作用は集合の持つ代数的な構造(群構造)と整合性のある作用だったおかげで各部分群の不変集合がその構造を保ってくれて議論がすっきりしました.
いつか書こうと思って1年放置していた話をいざ書き始めたら当初の想定よりも大分長くなってしまいました.こうして大学で習ったことを使った計算ができると楽しいですね.
最後まで読んでいただいてありがとうございました.
