曲線・曲面論1～種々の定義を線形代数で見直す～

106

　こんにちは，えだまめです．最近トイレに一人で行っていいようになりました．やったーー！カテーテルを入れて強制排尿→オムツツに漏らす→尿瓶にする→介護されながらトイレと来てやっと独り立ちですよ…！五か月かかった…ｗ　
　さて今回は曲線・曲面論の様々な定義を確認したのちに，それらを線形代数を使って見直していきたいと思います．本当は別の話をまとめようと思ったんですけどいきなりそれだと大変かと思い至り，前座でこの話をまとめています．リーマン幾何の種々の定義理解するのに役立つかも！？ていうか数学科の面々は大抵授業で避けては通れないと思うので，参考にしてもらえればと思います．
　あと連載にするつもりはなかったんですけど，3つほどに記事を分けると思います．曲線論，曲面論，見直し見たいな感じで．

平面の曲線論から

　まず弧長パラメータの方から説明していこう．いらないかなとも思ったが念のため．線積分を考える．２変数関数の積分だ．
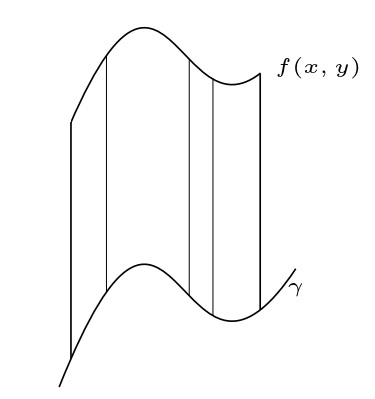遅くなったり早くなる積分
　平面上のパス$\gamma$をとったが、これがいったり来たりしたり突然早くなったり遅くなったりしたら，うまい積分ができなくなってしまう．いやでしょ？スカスカな積分結果ｗこういう事が起こらないように全ての曲線には単調増加で一定速度のパラメータがあると嬉しい．そのために定義されるのが曲線の長さをパラメータにしてしまおうという発想だ．

弧長パラメータ

$\gamma=(x,y) :[0,1]\rightarrow\mathbb{R}^2$を特異点がない連続曲線とする．
このとき，弧長$L(\gamma)$とは
$$L(\gamma) = \int_0^1 |\dot{\gamma}(t)|\ dt = \int_0^1\sqrt{\dot{x}^2+\dot{y}^2}\ dt $$
ここで$\dot{\gamma}=\frac{d\gamma}{dt}$を表す．上付き・は時間での微分だ．加えて，$0$から$u$までの弧長を以下で表す．
$$s(u) = \int_0^u \sqrt{\dot{x}^2+\dot{y}^2}\ dt$$
また逆写像定理より弧長$s(u)$をuの代わりにパラメータととることができ，これをパラメータとする曲線$\gamma(s)$を弧長パラメータを変数に持つ曲線や弧長パラメータ表示という．

本当に逆写像定理使えるの？とかそもそも逆写像定理って何？っていう疑問は後に解決するとして具体例を一個見てみよう．大抵ここでみんな詰まるらしいので具体例を確認するのは大事だ．可能なら手も動かしたい．

二次関数

$(t,t^2)$という曲線を$t \in [0,1]$でとる．このとき．
$$\begin{array}{rcl} s(u) &=& \int_0^u \sqrt{\dot{x}^2+\dot{y}^2}\ dt\\ &=& \int_0^u \sqrt{1+4t^2}\ dt \\ &=& \int_0^{\tan^{-1} 2u} \frac{1}{\cos \theta}\cdot\frac{1}{2\cos^2 \theta}\ d\theta \\ \end{array} $$
$\int \frac{1}{\cos^3\theta}\ d\theta = \frac{\sin \theta}{2\cos^2\theta} + \frac{1}{4}\log\left( \frac{1+\sin \theta}{1-\sin \theta} \right) +C$($C$は定数)より
$$\begin{array}{rcl} s(u) &=& \frac{1}{2}\left[\frac{\sin \theta}{2\cos^2\theta} + \frac{1}{4}\log\left( \frac{1+\sin \theta}{1-\sin \theta} \right)\right]_0^{\tan^{-1} 2u}\\ &=& \frac{1}{2} \left( \frac{2u}{2(1+4u^2)^{\frac{3}{2}}} + \frac{1}{4}\log\left( \frac{1+\frac{2u}{\sqrt{1+4u^2}}}{1-\frac{2u}{\sqrt{1+4u^2}}} \right) \right) \end{array} $$
$s(u)=2u+\frac{20}{3}u^3+\cdots$より(wolfarm alphaでテーラー展開した)$\frac{ds}{du}(0)=2$．逆写像定理より$u=u(s)$とできる．

ひどい目にあった…脳梗塞で手計算ができないんだってば！簡単な例をとったと思ったらそうでもなかったですねｗ基本的に弧長パラメータは具体的に求められるものではない．

直線の弧長パラメータ表示

直線の弧長パラメータ表示を計算で求め，直感に沿ってるか確かめろ．

逆写像定理の主張を書いておこう．証明はしない．

逆写像定理

$U \subset \mathbb{R}$を開集合，$F:U\rightarrow\mathbb{R}$を$C^r$-級関数とする．
$p\in U$としたとき$F'(p) \not = 0$なら$^\exists V \ni F(p)$の近傍，$^\exists G:V\rightarrow U$，$C^r$-級関数 s.t. $G\circ F = id_{G(V))}$, $F\circ G = id_V$

ようは微分が0に潰れなければ方程式が解けるということだ．方程式を解くというのは逆関数を求めることに値する．例えばさっきの例を見てみると
$$s(u)=\frac{1}{2} \left( \frac{2u}{2(1+4u^2)^{\frac{3}{2}}} + \frac{1}{4}\log\left( \frac{1+\frac{2u}{\sqrt{1+4u^2}}}{1-\frac{2u}{\sqrt{1+4u^2}}} \right) \right)$$
に$u(s)$を代入して$s$になればこの式が解けたと言えよう．まあ絶対に無理だが，逆写像定理からそういう写像の存在は確かめられる．もっと簡単な例なら$y=x^2$に$x=\sqrt{y}$を代入すれば$y$に戻るだろう．そういう写像が存在することの条件を書いているのが逆写像定理だ．え？強くね？と思っただろうか．強いのだ．
　さて弧長パラメータの存在が保証されているか確かめていこう．要は微分が0にならなければ良い．
$$\begin{array}{rcvl} s(u) &=& \int_0^u |\dot{\gamma}(t)| dt\\ \leadsto \frac{ds}{du}(u) &=& |\dot{\gamma}(u)| \not= 0 \end{array} $$
$|\dot{\gamma}(u)|=0$のときは特異点となるので考慮しなくていい．そんなものがあるのかと疑問に思ったら$(t^2,t^3)$をGeoGebraとかのグラフ描画ソフトに入れて計算してみればいい．
　ということで逆関数定理より弧長パラメータが存在する．この弧長パラメータを使う利点は他にもある．弧長パラメータで曲線を微分してみる．曲線を$\gamma(t)$とすると
$$\gamma':=\frac{d\gamma}{ds} = \frac{d\gamma /dt}{ds/dt} = \frac{\dot{\gamma}}{|\dot{\gamma}|}$$
より$|\gamma'|$は1になる．つまり速度が1となる．これは線積分で速度を一定にしたいという目的に合致している．(ちなみに$\gamma'$はベクトルであることに注意しておく．)また，これを内積$\langle \ ,\ \rangle$で表示して微分すると，
$$\begin{array}{crcl} &\langle \gamma' , \gamma’ \rangle &=& 1 \\ \leadsto&\langle \gamma'',\gamma'\rangle + \langle \gamma',\gamma''\rangle &=& 0 \\ \leadsto &2\langle \gamma'',\gamma'\rangle &=&0 \end{array}$$
となり，$\gamma'$と$\gamma''$は直交することが分かる．
　このトリック，所見だとずるいなぁと思うが慣れると便利なので知っておこう．
　$\gamma'$は当然曲線の微分なので接ベクトルになり，それに直交するベクトルは法ベクトルになる．この法ベクトルの大きさは1とは限らないので法方向の単位ベクトルを$\bm{n}$とおいて，$\gamma''$の大きさを$\kappa$と置くと，$\gamma'' = \kappa \bm{n}$と表せる．接方向を微分して出てきた大きさが$\kappa$であり，それが曲がり具合を表すので曲率という．
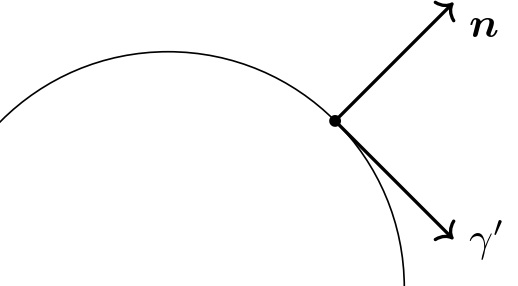法方向
　具体的な例を計算してみよう．

サイクロイド

$\gamma(t) = (t-\sin t,1-\cos t)$と置く．このときの曲率を求めよう．
$\frac{d\gamma}{dt} = 2 \sin \frac{t}{2}(\sin \frac{t}{2}, \cos \frac{t}{2})$より，$\frac{ds}{dt} = |\dot{\gamma}|=2|\sin \frac{t}{2}|$よって，
$$\frac{d\gamma}{ds} = \frac{\sin \frac{t}{2}}{|\sin \frac{t}{2}|}(\sin \frac{t}{2}, \cos \frac{t}{2})$$
また，二回微分を計算すると
$$\frac{d^2\gamma}{ds^2}=\frac{1}{|\dot{\gamma}|}\frac{d\gamma'}{dt}= \frac{1}{2|\sin \frac{t}{2}|}\frac{\sin \frac{t}{2}}{2|\sin \frac{t}{2}|}(\cos \frac{t}{2}, -\sin \frac{t}{2})$$
となりこのベクトルは$\gamma'$と直交している．また曲率は以下で与えられる．
$$\kappa = -\frac{1}{4|\sin \frac{t}{2}|}$$

本当は$\bm{n}$を正の方向で決めてから曲率を求める．この例の曲率の計算で飛躍を感じたとすればそこだろう．法方向の取り方として$\bm{n}$と$-\bm{n}$の取り方があるが，今回は行列式$|\gamma' \ \bm{n}|>0$となるように取っている．

パラメータ表示での法方向

$$\gamma'' = \frac{d}{ds}\frac{\dot{\gamma}}{|\dot{\gamma}|} = \frac{d}{dt}\frac{\dot{\gamma}}{|\dot{\gamma}|}\left / \frac{ds}{dt}\right. = \frac{1}{|\dot{\gamma}|}\left( \frac{\ddot{\gamma}|\dot{\gamma}|-\dot{\gamma}\frac{d}{dt}|\dot{\gamma}|}{|\dot{\gamma}|^2}\right)$$
曲率を求めたいときはこのベクトルの大きさを出せばいい．

直線

直線の接ベクトル，法ベクトル，曲率を出して直感と相違ないことを確かめろ．

円と楕円

物足りない人のためもう一問．円と楕円の曲率を出せ．

最後にフレネの公式を示してこの章を終わろう．

フレネの公式

$$\DVec{\gamma''}{\bm{n}'} =\left( \begin{array}{cc} 0 & \kappa\\ -\kappa & 0 \end{array}\right) \DVec{\gamma'}{\bm{n}}$$

つまり$\gamma'' = \kappa \bm{n}$，$\bm{n}'=-\kappa \gamma'$を示せばいいが，前者は定義通りなので後者を示す．$\bm{n}$の大きさは単位ベクトルだから1なので
$$\langle \bm{n}, \bm{n}\rangle = 1 \ \ \leadsto\ \ \langle \bm{n}', \bm{n}\rangle = 0$$
より，法方向の微分は法方向と直交している．よって$\bm{n}'=k\gamma'$と書けるが，$\langle \gamma', \bm{n}\rangle = 0$より，これを微分して
$$ 0=\langle \gamma'', \bm{n}\rangle + \langle \gamma, \bm{n}'\rangle = \kappa+k$$
より従う．

この定理ピカールの逐次近似法と相性が良くて曲線の局所表示を得るのに便利なんだよなぁ…あと特異点が絡むと$\frac{t^n}{n}$弧長パラメータってのが出てきてめちゃくちゃきれいにうまく行くって話はまた今度．

空間の曲線論から

　同様に弧長パラメータを定義して曲率とかを求めたい．ただし，空間内なため張られるベクトルが3本ある．平面は２本だけだったので$\gamma'$と$\bm{n}$でよかったがこれに一本追加する必要がありそうだ．同様に曲線を微分していく．
　$|\gamma'|=1$なのは変わらないため同様のトリックにより，
$$\langle \gamma', \gamma' \rangle = 1 \ \ \leadsto\ \ \langle \gamma'', \gamma' \rangle = 0$$
となり，このベクトルの大きさを曲率$\kappa$と置く．

フレネ・セレ枠と曲率・捩率

$\bm{e} = \gamma', \ \bm{n} = \frac{\bm{e}'}{|\bm{e}'|},\ \bm{b} = \bm{e}\times\bm{n}$の３つのベクトルの組をフレネ・セレの枠という．また$|\bm{e}'|$を曲率$\kappa$，$\langle \bm{n}',\bm{b} \rangle$を捩率$\tau$と置く．加えて，$\bm{e}$を単位接ベクトル，$\bm{n}$を主法線ベクトル，$\bm{b}$を従法線ベクトルという．

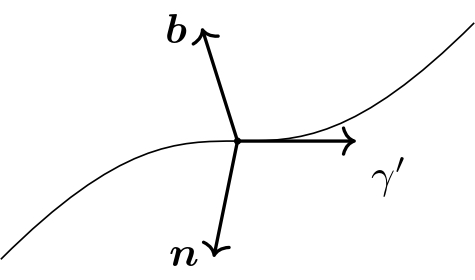主法線ベクトルと従法線ベクトル
　要は捩率とは$\bm{n}'$の$\bm{b}$方向の大きさを表している．そしてここで外積$\times$が出てきた．数学科だとなかなか出てこないがあんまり説明しすぎると冗長になってしまうので手短に．$\bm{x}\times \bm{y}$とは$\bm{x}$と$\bm{y}$に垂直であり，$\bm{x}$と$\bm{y}$が張る平行四辺形の大きさが外積の大きさになる．重要なのは直交してるということと，直交している単位ベクトルの外積は大きさが1になる．
　具体例を見てみよう．

螺旋

$\gamma = (a\cos t , a\sin t , bt)$，$ab\not=0$とする．(GeoGebraとかで描いて本当に螺旋になるか確かめてみよう)この曲線の捩率まで求める．
$$\begin{array}{rcl} \dot{\gamma} &=& (-a\sin t, a\cos t , b)\\ \end{array}$$
となるので$|\dot{\gamma}|=\sqrt{a^2+b^2}$となる．よって，
$$\begin{array}{rcccl} \bm{e} &=&　\frac{d\gamma/dt}{ds/dt} &=& \frac{1}{\sqrt{a^2+b^2}}(-a\sin t, a\cos t , b)\\ \bm{n} &=&　\frac{d\bm{e}/ds}{|d\bm{e}/ds|} &=& \frac{a}{|a|} (-\cos t,-\sin t,0) \\ \bm{b} &=& \bm{e}\times \bm{n} &=& \frac{a}{|a|\sqrt{a^2+b^2}}(b\sin t, -b\cos t,a) \end{array}$$
となる(それぞれの大きさが1なことを確認せよ).

$$\begin{array}{rcl} \bm{e}' &=& \frac{1}{\sqrt{a^2+b^2}} \cdot \frac{a}{\sqrt{a^2+b^2}}(-\cos t, -\sin t , 0)\\ &=& \frac{|a|}{a^2+b^2} \cdot \frac{a}{|a|}(-\cos t, -\sin t , 0) \end{array}$$
より，曲率は$\frac{|a|}{a^2+b^2}$となる．
$$\begin{array}{rcl} \bm{n}' &=& \frac{1}{\sqrt{a^2+b^2}} \cdot \frac{a}{|a|}(\sin t, -\cos t , 0) \\ \leadsto \langle \bm{n}',\bm{b}\rangle &=& \frac{1}{a^2+b^2} \cdot \frac{a^2}{|a|^2}(b\sin^2 t + b\cos^2 t)\\ &=& \frac{b}{a^2+b^2} \end{array}$$
と捩率が得られる．ちなみに，$|\bm{n}|=1$より
$$\langle \bm{n},\bm{n} \rangle = 1 \ \leadsto \ \langle \bm{n}',\bm{n} \rangle = 0$$
より，$\bm{n}'$は$\bm{n}$の成分を持たない．また$\bm{e}$の成分を求めてみよう．成分を$k$と置くと
$$\begin{array}{rcl} |\bm{n}' \ \bm{n} \ \bm{b}| &=& |k\bm{e}+\tau\bm{b} \ \bm{n} \ \bm{b}|\\ &=& |k\bm{e} \ \bm{n} \ \bm{b}|\\ &=& k \cdot \frac{1}{a^2+b^2} \left|\begin{array}{ccc} -a\sin t & a\cos t & b\\ -\cos t & -\sin t & 0\\ b\sin t & -b\cos t & a \end{array}\right| \\ &=& k\frac{1}{a^2+b^2}\cdot (a^2\sin^2 t+b^2\cos^2t-(-b^2\sin^2t-a^2\cos^2t))\\ &=& k \end{array}$$
また，
$$\begin{array}{rcl} |\bm{n}' \ \bm{n} \ \bm{b}| &=& \frac{1}{a^2+b^2}\cdot \frac{a}{|a|} \left|\begin{array}{ccc} \sin t & -\cos t & 0\\ -\cos t & -\sin t & 0\\ b\sin t & -b\cos t & a \end{array}\right| \\ &=& \frac{1}{a^2+b^2}\cdot \frac{-a^2}{|a|}\\ &=& \frac{-|a|}{a^2+b^2}\cdot \frac{a^2}{|a|^2} \ = \ -\kappa\\ \end{array}$$
よって$k=-\kappa$を得る．つまり$\bm{n}'=-\kappa\bm{e}+\tau\bm{b}$となることが分かる．
　一般に直交した単位ベクトルの組$\{ \bm{u},\bm{v},\bm{w}\}$と置くと，あるベクトル$\bm{a} = x\bm{u} + y\bm{v} + z\bm{w}$の$\bm{u}$の成分を求めたくば行列式$|\bm{a}\ \bm{v}\ \bm{w}|$を求めればいい．証明をすると以下のようにすればいい．
$$\begin{array}{rcl} |\bm{a}\ \bm{v}\ \bm{w}| &=& |x\bm{u} + y\bm{v} + z\bm{w}\ \bm{v}\ \bm{w}|\\ &=& x\cdot |\bm{u}\ \bm{v}\ \bm{w}| \ = \ x \end{array}$$

　最後に紹介した行列式を使った公式が先生の論文に断りなく出てきた．たぶん当たり前なのだろう．こわい．

パラメータ表示

自分で計算したい人のために問題を残しておこう．直線でまず定義とかを確かめた後にやってほしい．空間曲線$\gamma$に対していかが成り立つことを示せ．
$$\bm{e} = \frac{\dot{\gamma}}{|\dot{\gamma}|}, \ \ \bm{n} = \frac{(\dot{\gamma}\times\ddot{\gamma})\times\dot{\gamma}}{|(\dot{\gamma}\times\ddot{\gamma})\times\dot{\gamma}|}, \ \bm{b}=\frac{\dot{\gamma}\times\ddot{\gamma}}{|\dot{\gamma}\times\ddot{\gamma}|}$$
$$\kappa = \frac{|\dot{\gamma}\times\ddot{\gamma}|}{|\dot{\gamma}|^3}, \ \tau = \frac{\det (\dot{\gamma}, \ \ddot{\gamma},\ \dddot{\gamma})}{|\dot{\gamma}\times\ddot{\gamma}|^2}$$

空間アステロイド

作った公式を使ってみたいときようにこの問題を残しておく．もちろんこの公式を作ってなくても解けるだろう．
$\gamma=(\cos^3 t, \sin^3t, \cos 2t)$の捩率まで全て求めよ．(あとGeoGebraなどで描画せよ)

　さて次ににフレネ・セレの公式を示そう．

フレネ・セレの公式

$$\left(\begin{array}{c} \bm{e}'\\ \bm{n}'\\ \bm{b}'\\ \end{array}\right) = \left(\begin{array}{ccc} 0 & \kappa & 0\\ -\kappa & 0 & \tau\\ 0 & -\tau & 0\\ \end{array}\right) \left(\begin{array}{c} \bm{e}\\ \bm{n}\\ \bm{b}\\ \end{array}\right)$$

　つまり$\bm{e}'=\kappa\bm{e}$，$\bm{n}'=-\kappa\bm{e}+\tau\bm{b}$，$\bm{b}'=-\tau\bm{n}$を示せばいい．最初は定義から明らかである．2番目は螺旋の例で成り立つことを確認した．もちろん一般の場合で示すが．

$\bm{n}'=a_1\bm{e} +a_2\bm{n}+a_3\bm{b}$と置く．定義から$a_3=\tau$である．またいろんな式を微分していく．
$$\begin{array}{ccl} \langle \bm{n},\bm{n} \rangle=1 &\leadsto& \langle \bm{n}',\bm{n} \rangle=0 \\ &\leadsto& a_2=0\\ \langle \bm{e},\bm{n} \rangle=0 &\leadsto& \langle \bm{e}',\bm{n} \rangle + \langle \bm{e},\bm{n}' \rangle = 0\\ &\leadsto& \kappa + a_1 = 0 \end{array}$$
以上より$\bm{n}'=-\kappa\bm{e}+\tau\bm{b}$を得る．
同様に$\bm{b}'=b_1\bm{e}+b_2\bm{n}+b_3\bm{b}$と置いて種々の式を微分していく．
$$\begin{array}{ccl} \langle \bm{b},\bm{e} \rangle = 0 &\leadsto& \langle \bm{b}',\bm{e} \rangle + \langle \bm{b},\bm{e}' \rangle = 0 \\ &\leadsto& 0 = b_1 + \langle \bm{b},\kappa\bm{n} \rangle = b_1\\ \langle \bm{b},\bm{n} \rangle=0 &\leadsto& \langle \bm{b}',\bm{n} \rangle + \langle \bm{b},\bm{n}' \rangle = 0\\ &\leadsto& 0 = b_2 + \langle \bm{b},-\kappa\bm{e}+\tau\bm{b} \rangle = b_2 + \tau\\ \langle \bm{b},\bm{b} \rangle=1 &\leadsto& \langle \bm{b}',\bm{b} \rangle = 0 \\ &\leadsto& b_3=0\\ \end{array}$$
以上より$\bm{b}'=-\tau\bm{n}$を得る．

　ちなみに$\mathbb{R}^n$上の曲線も弧長パラメータで微分することで枠を作り出すことができる．また，フレネ・セレの公式の類似物もきちんと出てくる．
　最後に大切な定理を示して終わろう．

空間曲線の基本定理

区間$[0,1]$で定義された正値関数$\kappa(s)$と関数$\tau(s)$が与えられたとき，$s$を弧長パラメータとする曲線で$\gamma(s)$で曲率が$\kappa(s)$，捩率が$\tau(s)$となるものが存在する．また，そのような曲線は回転と平行移動を除いて唯一である

　最初に意義を説明しよう．所見だとまあ当たり前だろ~で流してしまいがちだが幾何の大切な考え方が多分に含まれている．
　まず平行移動や回転を除いてというのが合同変換で同じということだ．幾何学とはある同じという設定の上でおんなじ物を探求したり，違うならその特徴量は何かを探求する学問だ．ここの曲線論は合同変換で写りあうものを同じとしているから，曲率と捩率を与えれば曲線が唯一に定まるのだ．
　また，そのように合同変換で写りあう曲線によっては変わらないものを不変量という．上で言った特徴量の一つだ．この定理は曲率と捩率が曲線の不変量であることを主張している．また．曲率と捩率をテーラー展開したものを考えれば自然数濃度の不変量を考えることができる．まあそれだけでは曲線を確定できないのだが．詳しくはフラットな関数について考察するといい．もちろん不変量にあることは変わらない．
　では，証明をしていこう．常微分方程式の解の存在性と唯一性を使うためそれは既知とする．知らんかったら調べたうえで「はへ～そんなのがあるんか～」顔をしてればいい．

3次行列を値に持つ関数$F(s)$が，常微分方程式
$$F'(s) = F(s)K(s),\ K(s)=\left(\begin{array}{ccc} 0 & -\kappa(s) &0 \\ \kappa(s) &0 &-\tau(s)\\ 0 &\tau(s) &0 \end{array}\right)$$
を満たすとする．初期条件$F(0)=I$(3次の単位行列)の下で，この微分方程式は解を一意的に持つ．
$$\begin{array}{rcl} (F(s)^t F(s))' &=& F'(s)^t F(s) + F(s)^tF'(s)\\ &=& F(s) \left( K(s)+K(s)^t \right)F(s)\\ &=& F(s) \left( \left(\begin{array}{ccc} 0 & -\kappa(s) &0 \\ \kappa(s) &0 &-\tau(s)\\ 0 &\tau(s) &0 \end{array}\right) + \left(\begin{array}{ccc} 0 & \kappa(s) &0 \\ -\kappa(s) &0 &\tau(s)\\ 0 &-\tau(s) &0 \end{array}\right) \right)F(s)\\ &=& 0 \end{array}$$
より，微分が0なため元の関数は$s$によらない定数行列になる．つまり$F(s)F(s)^t=I$となり，$F(s)$は直交行列になる．定数倍は最初から$F(s)$に割り振って議論すればいい．
　$F(s)=(\bm{e}(s),\ \bm{n}(s),\ \bm{b}(s))$と書くと，$\{\bm{e}(s),\ \bm{n}(s),\ \bm{b}(s)\}$は正規直交枠であり，
$$\gamma(s) = \int_0^s \bm{e}(t)\ dt$$
が求める曲線である．一意性の主張は微分方程式の解の一意性の帰結である．