微分方程式f'(x)=f(-x)を解く

問題

見た目はすごくシンプルな微分方程式です。
これだけシンプルなら、高度な質問応答システムである Wolfram Alpha であっさり答えを出してくれるでしょう。

「f'(x)=f(-x)」と入力してポチッ・・・

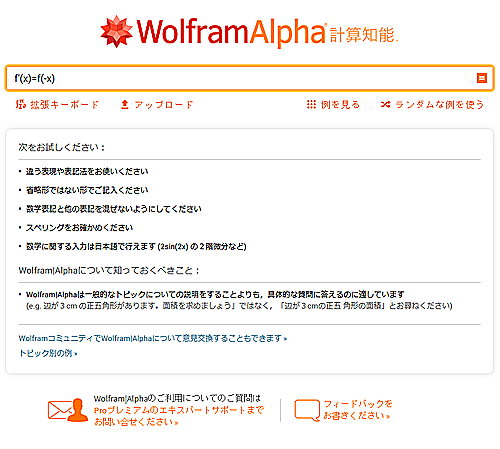Wolfram Alphaのf'(x)=f(-x)の結果

宇宙ネコ

／(^o^)＼ﾅﾝﾃｺｯﾀｲ

$f'(x)=f(-x)$は解いてくれませんでした。

$f'(x)=f(x)^2-x$のように$x,f(x),f'(x),f''(x),\cdots$の組み合わせでできている式の場合には解こうとしてくれるのですが、$f(-x)$が含まれているとうまくいきません。そもそも微分方程式ではなく「わけのわからないもの」と認識されたようです。(2020/11/24現在)

では、どうやって解けばいいのでしょうか。皆さんも考えてみましょう。

答え

原始関数や微分方程式は、積分して求めるものですが、$f'(x)=f(-x)$ではどうしようもないように見えます。
そこで、「押してダメなら引いてみろ」という格言のように、積分の前に微分することを考えます。

$f(x)$は微分可能なので、$f(-x)$も当然、微分可能です。よって、$f'(x)$も微分可能です。
(つまり$f(x)$は$2$階微分可能・・・というかもっと言えば無限回微分可能です。)

$f'(x)=f(-x)$の両辺を微分してみると、

\begin{eqnarray*} f''(x) & = & \frac{d}{dx}f(-x) & \quad(\leftarrow\ \frac{d}{dx}f(-x)は、「f(-x)のxにおける導関数」の意味。) \\[5pt] & = & f'(-x)\times \frac{d}{dx}(-x) & \quad(\leftarrow\ 合成関数の微分。f'(-x)は、「f(x)の-xにおける微分係数」の意味。) \\[5pt] & = & -f'(-x) & \quad(\leftarrow\ \frac{d}{dx}(-x)=-1) \\[8pt] & = & -f(x) & \quad(\leftarrow\ f'(x)=f(-x)のxを-xに置き換えたf'(-x)=f(x)を使う。) \end{eqnarray*}

したがって、$f''(x)+f(x)=0$であることがわかりました。
定数係数の$2$階線形微分方程式に帰着できました。
この微分方程式なら簡単です。いつもの特性方程式を解けば答えが出ます。(知らない方は こちら を読めば大丈夫です。)

$f''(x)+f(x)=0$を解くと$f(x)=A\cos(x)+B\sin(x)\ (A,Bは任意定数)$になります。
これはまだ求めたい一般解ではありません。
$f'(x)=f(-x)$を使って、定数$B$を$A$を使って表します。

\begin{eqnarray*} f'(x) & = & f(-x) & \\ (A\cos(x)+B\sin(x))' & = & A\cos(-x)+B\sin(-x) & \\ -A\sin(x)+B\cos(x) & = & A\cos(x)-B\sin(x) \end{eqnarray*}

これがすべての$x$で成り立っていなければならないので、$B=A$となります。

よって、求める解は$f(x)=A(\cos(x)+\sin(x))\ (Aは任意定数)$です。

おわりに

なんとか$f'(x)=f(-x)$の一般解を求めることができました。
Wolfram Alphaに勝った感じがして気分がいいですね()

最後に類題を$2$問置いておくので、やってみたい人は下の解答を見ないでチャレンジしてみてください。

以上、読んでいただきありがとうございました。