数学を愛する会さんのTwitterの問題を解いてみました

数学を愛する会 さんがTwitterで出題していた問題( こちら )を解きました。ゴリ押しです。

次のように座標をとります。
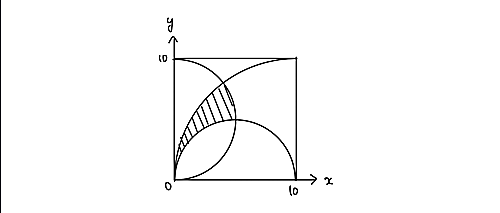xy座標
すると、求める面積は、
$$ A=\{(x,y)|(x-5)^2+y^2\geq 5^2\}\\ B=\{(x,y)|x^2+(y-5)^2\leq 5^2\}\\ C=\{(x,y)|(x-10)^2+y^2\leq 10^2\} $$
とするとき、
$$ S=\int \int_{A \cap B \cap C} dxdy $$
で表されます。中心をすべて軸上に持ってきたのがミソです。極座標変換しましょう。$x=r\cos \theta, y=r\sin \theta,(r\geq 0,\theta\in [0,2\pi])$とすると、$A,B,C$はそれぞれ、
$$ A'=\{(r,\theta)|r\geq 10\cos \theta\}\\ B'=\{(r,\theta)|r\leq 10\sin \theta\}\\ C'=\{(r,\theta)|r\leq 20\cos \theta\} $$
となり、
$$ S=\int \int_{A' \cap B' \cap C'}rdrd\theta $$
となりました。$A' \cap B' \cap C'$を図示すると、次のようになります。
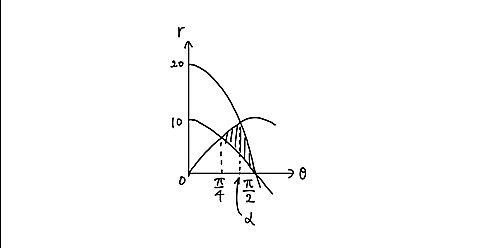rθ座標
したがって、$20\cos \theta=10\sin \theta$を満たす$\theta\in [\pi/4,\pi/2]$を$\alpha$とおくと、
$$ S=\int_{\theta=\pi/4}^{\theta=\alpha} \int_{r=10\cos \theta}^{r=10\sin \theta}rdrd\theta+ \int_{\theta=\alpha}^{\theta=\pi/2} \int_{r=10\cos \theta}^{r=20\cos \theta}rdrd\theta\\ =\cdots\\ =-250\cos^2\alpha+25+75\left(\frac{\pi}{2}-\alpha\right)\\ =75\arctan\left(\frac12\right)-25 $$
と、求まりました。