ドラゴン曲線を描く

ドラゴン曲線を描画する話。
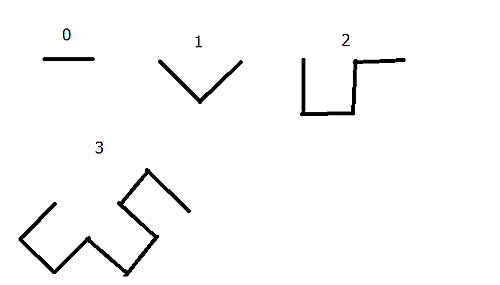
　まず、ドラゴン曲線とは次のようなもの。
ドラゴン曲線
左下の端っこが途切れているところからスタートして、方向を変化させながら進んでいく感じ（canvas2Dでの描画なので回転方向が時計回り、まあどっちでもいいんだけど）。
とりあえずオリジナルの定義。$0, 1, \cdots, 7$で、$8$つの等分された方向をあらわすとする。つまり、$k$で
$$\left(\cos\frac{k\pi}{4},~\sin\frac{k\pi}{4}\right)$$
があらわすベクトルの方向に点が進むことを表現する。このときたとえば、
$$[0, 2, 4, 2]$$
という配列は、右、上、左、上という順番で進むことをあらわす。つまり$\mathrm{mod}~8$で考えているのでそのように計算する（$8=0$とか$4+5=1$とか）。

フラクタル図形としてのドラゴン曲線はこうじゃないけど、すべてのセグメントが同じ長さとしたときのものを考えているのでこんな感じになる。
　この定義だとどんどん長くしていくのが困難で規則も見出しづらいので、スタートが$0$になるように定義を改造する。すなわち、前半の$-1$をやめて後半を$+2$するように変更する。
$$[a_0,a_1,\cdots,a_{n-1}]~\to~[a_0,a_1,\cdots,a_{n-1},a_{n-1}+2,\cdots,~a_1+2,~a_0+2].$$
すなわち後半は逆配列にして$+2$する。$+2$とは$90$°回転に相当する。
　これを$2$回行うとどうなるのか見るため、長い部分をギリシャ文字で置き換えて考えてみる。配列$\alpha$の逆並びを$\overline{\alpha}$のように書く。あと逆配列ですべて$+2$したものを$\overline{\alpha}+2$と書くなど。$\overline{\alpha + 2} = \overline{\alpha}+2$とか明らかね。
$$[\alpha]~\to~[\alpha,~\overline{\alpha}+2]~\to~[\alpha,~\overline{\alpha}+2,~\overline{\overline{\alpha}+2}+2,~\overline{\alpha}+2]$$
となるがここで
$$\overline{\overline{\alpha}+2}+2 = \overline{\overline{\alpha}}+4=\alpha +4$$
なので方向が真逆になる。これを${\alpha}'$と書くことにすると、結局、
$$[\alpha,~\beta]~\to~[\alpha,~\beta,~\alpha',~\beta]$$
のようになっている。これは一般的に成り立つ。なぜならどの段階においても$\beta$の部分は$\alpha$の部分に対してあのような表記になっているから。
　このことを用いると、項数を使うことでどの方向に曲がるのかを計算できる。第$n$項を考える。$n=0,1$ならば$0,2$になる。最初の$4$項は、
$$[0,~2,~4,~2].$$
$n\geq 2$とする。$n$に対し、$2^m\leq n <2^{m+1}$となる$m$を取る。このとき$n$は$2^{m+1}$まで作った配列の後半に入っている。上記の議論で言うと後ろの$[\alpha',~\beta]$の方。だからそこでもし$2^m\leq n <2^m + 2^{m-1}$に入るならこれは第$n-2^m$項目を反転させたもの（$4$を足したもの）になるし、$2^m+2^{m-1}\leq n < 2^{m+1}$ならそのまま第$n-2^m$項目の値になる。計算としては、$n$の$2$進数展開において一番頭の$1$を取り去る処理に当たる。
　これを繰り返すといずれ$0$か$1$になって$m$が取れなくなる。そこまでに何回反転をしたかで、第$n$項が何であったかが分かる。反転回数を$t$とすると、最後に$0$になるなら$4t$だし、$1$になるなら$4t+2$ということになる。ところでこの$2^m$を取り去る行為において後半のどちらに入っているかというのは、頭の$1$の下が$0$か$1$かということに相当する。だから、$11$の並びなら反転しないし、$10$の並びなら反転させるというわけ。

例えば
$154=10011010_{(2)},~~~155=10011011_{(2)}$
なので$154$番目の曲がる方向は$4\cdot 3=12=4$でまっすぐ左。$155$番目は$4\cdot 2+2=10=2$だから上方向。canvas2Dなら下だけど。
　こうなるともう$8$分割にこだわる必要がないので、$90$°ベースで考える。また、このあとコードを載せたいので回転方向は時計回りにする。
　自分はよくp5.jsという描画ライブラリを使うので、それによる描画コードを載せる：

      let a = 0;
let b = 0;
let f = 0;
function setup(){
    createCanvas(640, 640);
    background(0);
    stroke(255);
}

function draw(){
    translate(320, 320);
    let dir = f & 1;
    let h = 1;
    while(f >= h){
        if(!(f & h) && (f & (h * 2))){ dir += 2; }
        h *= 2;
    }
    let s = 8 * cos(dir * PI / 2);
    let t = 8 * sin(dir * PI / 2);
    line(a, b, a + s, b + t);
    a += s;
    b += t;
    f++;
}
    

作品のリンク
描画結果：
ドラゴン曲線3
中央上の切れたところからスタートしている。点$(a,~b)$が指定された方向に毎フレーム移動する感じ。次に進む方向を$(s,~t)$というか$dir$が与える。$90$°ベースなので$dir$に$\pi/2$を掛ける。項数はフレームの$f$が担う。$f$の初期値は$2$進数展開での$1$の位だから$1$と&を取って出す。そのあとは$h$というのが$1$から始まって次第に$2$倍される、これが$f$以下の範囲で。$h$と$2h$はそれぞれ$f$の$2$進展開での$2$つの連続した位に相当してて、$2h$の位が$1$で$h$の位が$0$のときに$dir$を$180$°の分だけずらしている（すなわち$+2$している）。これが「$10$」の並びの数だけ反転、に相当するから、ちゃんと上で述べた通りの描画になっている。
短く書くとこんな感じ：

      w=640;a=b=f=k=0;c=320
setup=()=>{createCanvas(w,w);background(0);k=PI/2}
draw=()=>{translate(c,c);e=f&1;h=1;while(f>=h){if(!(f&h)&&(f&(h*2))){e+=2}h*=2}s=8*cos(k*e);t=8*sin(k*e);stroke(w);line(a,b,a+=s,b+=t);f++}
    

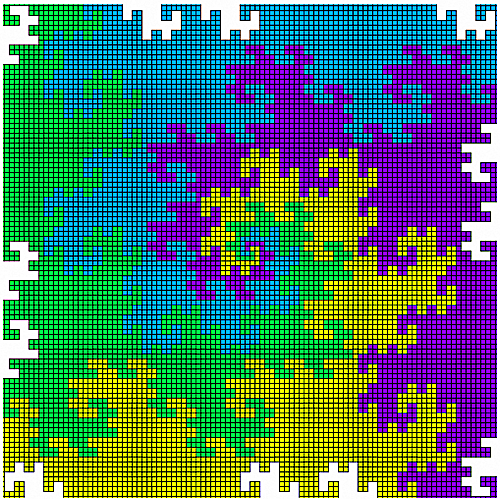
これは実は$4$つの方向に進ませるとすべての格子で平面を覆うことができる。そのようにしたコードがこちら。

      w=640;a=b=f=k=0;c=320
setup=()=>{createCanvas(w,w);background(0);k=PI/2}
draw=()=>{translate(c,c);e=f&1;h=1;while(f>=h){if(!(f&h)&&(f&(h*2))){e+=2}h*=2}s=8*cos(k*e);t=8*sin(k*e);r=4;while(r--){rotate(k);stroke(r*90,(r&1)*w,w);line(a,b,a+s,b+t)}a+=s;b+=t;f++}
    

作品のリンク
実行結果：
ドラゴン曲線4
すなわちすべての隣接格子点間のセグメントを$1$回だけ通るので、それを、そのセグメントを対角線とする正方形で置き換えれば完全に平面充填できる。それを実行したコードがこちら。

          let w = 640;
    let a = 320;
    let b = 320;
    let f = 0;
    function setup(){
        createCanvas(w, w);
        colorMode(HSB, 64);
    }
    function draw(){
        let e = (f & 1) * 2 - 1;
        let h = 1;
        while (f >= h) {
            if (!(f & h) && (f & (h * 2))) {
                e += 4;
            }
            h *= 2;
        }
        let s = 9 * cos(PI * e / 4);
        let t = 9 * sin(PI * e / 4);
        let r = 5;
        while (--r) {
            applyMatrix(0, -1, 1, 0, 0, w);
            fill(r * 12, w, w);
            quad(a, b, a, b + t, a + s, b + t, a + s, b);
        }
        a += s;
        b += t;
        f++;
    }
    

ドラゴン曲線6

曲線を描くだけなら最終的にこのくらい短く書ける(p5js)。

DragonCurve

      a=b=180;f=0;draw=_=>{k=PI/2;if(!f){createCanvas(640,640)}e=f&1;h=1;while(f>=h){if(!(f&h)&&(f&(h*2))){e+=2}h*=2}line(a,b,a-=8*cos(k*e),b+=8*sin(k*e));f++}
    

差分に着目したらもっと短くなった。

      x=y=180;u=8;v=f=0;draw=_=>{if(!f){createCanvas(640,640)}line(x,y,x-=u,y+=v);s=++f;while(1-s%2){s/=2}k=1-(s&2);z=u;u=-k*v;v=k*z}