準同型定理をお気持ち理解できる記事
この記事の目的と背景
こんにちは．mito_nyaです．
この記事では，代数学の基本から入り，最終的に準同型定理のお気持ちを理解することを目的としています．非常に平易に，丁寧に進めますので，どなたでも読むことができると思います．
Mathlogを使うのは初めてですのが，見苦しい部分もあると思いますが，ご了承ください．それでは，本題に入りたいと思います．
モチベーション
この講義では「空間は平面の積み重ね」であるということを定式化することを目標とします．
記法
この記事において，
- $\mathbb{R}$で実数全体の集合
- $\mathbb{R}_{>0}$で正の実数全体の集合
- $\mathbb{Z}$で整数全体の集合
- $\mathbb{N}$で自然数全体の集合
を表すものとします．
また，記号「$:=$」は，「左辺のものを右辺のもので定義する」という意味です．たとえば，$f(x):=x^2$と書くと，関数$f(x)$を$f(x)=x^2$と定義する，という意味になります．
準備
群とは？
この章では，代数の基本概念である「群」を説明します．既知の方は読み飛ばしていただいて構いません．
集合$G$が演算$+$に関して群であるとは，次を満たすことをいう：
- $a\in G$，$b\in G$のとき$a+b\in G$である．
- $a\in G$，$b\in G$，$c\in G$のとき$(a+b)+c=a+(b+c)$が成り立つ．
- 次を満たす$0\in G$が存在する(単位元の存在)：
任意の$a\in G$に対して$a+0=0+a=a$が成り立つ． - 任意の$a\in G$に対し次を満たす$b\in G$が存在する(逆元の存在)：
$a+b=b+a=0$．
$\mathbb{R}$は加法に関して群をなします．また，0でない実数全体の集合は乗法に関して群をなします．
また，$\mathbb{N}$は加法に関して群ではありません(単位元・逆元が存在しない)．
「等しい」という概念を拡張する
この章では「同値関係」を定義します．
集合$G$における関係$\sim$が次を満たすとき，$\sim$は同値関係であるという．
- $a\sim a$が成り立つ．
- $a\sim b$ならば$b\sim a$である．
- $a\sim b$，$b\sim c$ならば$a\sim c$である．
$\mathbb{R}$における$"="$は同値関係です．また，$\mathbb{R}$における$a\sim b$を「$a-b$が整数のとき」と定めるとこれは同値関係です．さらに，平面ベクトル全体$$
\left\{ \left. \begin{eqnarray}
\left(
\begin{array}{c}
a \\
b
\end{array}
\right)
\end{eqnarray} \right|a\in\mathbb{R}, b\in\mathbb{R}\right\}
$$において，
$$
\begin{align}
\begin{pmatrix}
a \\
b
\end{pmatrix}
\sim
\begin{pmatrix}
c \\
d
\end{pmatrix}
\end{align}
$$を
$$
\begin{align}
\begin{pmatrix}
a \\
b
\end{pmatrix}
=k
\begin{pmatrix}
c \\
d
\end{pmatrix}
\end{align}
$$を満たす$k$が存在する，と定義するとこれは同値関係です．
さらに，集合$G$を同値関係$\sim$で「割る」ことができます．
$a\in G$に対して$[a]:=\left\{\left.b\in G\right|a\sim b\right\}$と表す．$[a]$を$a$の同値類といい，$G/\sim:=\left\{\left.[a]\right|a\in G\right\}$と定める．
$\mathbb{Z}$に同値関係$n\sim m$を「$n-m$が5の倍数」と定めます．このとき，$\mathbb{Z}/\sim=\{[0], [1], [2], [3], [4]\}$です．
群としての「構造を保つ」写像を考える
まずは写像を定義しておきます．
$X$，$Y$を集合とする．$f$が$X$から$Y$への写像であるとは，任意の$x\in X$に対して，$y=f(x)$となる$y\in Y$が一意に定まることをいう．また，これを$f:X\to Y$と書く．
$f(u, v)=u+v\quad(u\in\mathbb{R}, v\in\mathbb{R})$とすると，$f$は$\mathbb{R}^2=\{(x, y)|x\in\mathbb{R}, y\in\mathbb{R}\}$(実数の2次元)から$\mathbb{R}$への写像です．
関数は写像の一種です．
次に準同型写像を定義します．
$(X, +)$，$(Y, \times)$をそれぞれ群とし(つまり集合$X$は演算$+$について群，集合$Y$は演算$\times$について群)，$f:X\to Y$とする．
このとき，$f:X\to Y$が準同型写像であるとは，次を満たすことをいう：
- 任意の$a\in X$，$b\in X$に対し，$f(a+b)=f(a)\times f(b)$
$X$を収束する実数列，$Y$を実数とすると，$(X, +)$，$(Y, +)$はそれぞれ群です．写像$f:X\to Y$を収束列の極限をとるよう定義すると，次が成り立ちます．
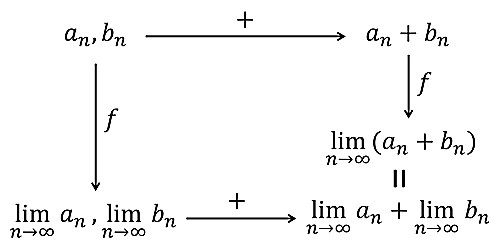準同型写像のイメージ
準同型写像のイメージは，同型写像のイメージとともに後述します．
群として「同じ」であること
では，同型写像を定義します．
$(X, +)$，$(Y, \times)$をそれぞれ群とし，$f:X\to Y$とする．
このとき，$f:X\to Y$が同型写像であるとは，次を満たすことをいう：
- $f:X\to Y$は準同型写像
- $f:X\to Y$は全単射
すなわち，任意の$y\in Y$に対しても$y=f(x)$となる$x\in X$が一意に存在する．
ようするに，集合$X$と$Y$の間に過不足がない，ということです．
$f:\mathbb{R}^2\to\mathbb{R}\quad f(u, v)=u+v$は同型写像でないです．なぜならば，たとえば，$1\in\mathbb{R}$に対し，$f(1, 0)=1$，$f(0, 1)=1$，$f(-1, 2)=1$，……というように対応が1対1でない(全単射でない)からです．
次に同型を定義します．
$(X, +)$，$(Y, \times)$をそれぞれ群とし，$f:X\to Y$を同型写像とする．このとき$X$，$Y$は群として同型であるといい，$X\cong Y$とかく．
これは$(X, +)$と$(Y, \times)$が同一視できることを意味します．
$(\mathbb{R}, +)$と$(\mathbb{R}_{>0}, \times)$は同型です．$f(x)=e^x$とします．
- $f(x+y)=e^{x+y}=e^x\times e^y=f(x)\times f(y)$(準同型性)
- 任意の正の数$r$に対し$\log r\in\mathbb{R}$で，$f(\log r)=e^{\log r}=r$です．よって$f$は同型写像といえます．
以上より，$(\mathbb{R}, +)$と$(\mathbb{R}_{>0}, \times)$が同型であることがいえました．
では，先述したとおり，準同型写像と同型写像のイメージを紹介します．
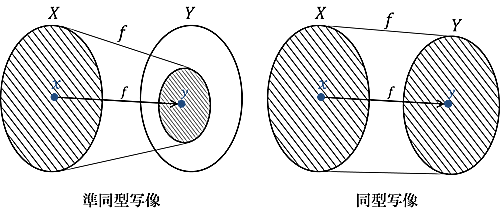イメージ
準備の最後に核と像を定義します．
$(X, +)$，$(Y, \times)$をそれぞれ群とし，$f:X\to Y$を準同型写像とする．
$f$の核$\mathrm{Ker}(f)$を$\mathrm{Ker}(f)=\{x\in X|f(x)=1\}$で定める(ここにおける"1"は，群$(Y, \times)$における単位元を表す)．
$f$の像$\mathrm{Im}(f)$を$\mathrm{Im}(f)=\{y\in Y|f(x)=yなるx\in Xが存在\}$とする．
$f$が同型ならば，$\mathrm{Ker}(f)=\{0\}$，$\mathrm{Im}(f)=Y$となります．
核と像のイメージは次の通りになります．
核と像
$X$を整数全体，$Y$を$\{0, 1, 2\}$，写像$f:X\to Y$を「$x$を3で割った余り」と定めます．このとき，$\mathrm{Im}(f)=\{0, 1, 2\}$，$\mathrm{Ker}(f)=\{3の倍数全体\}$です．
ここで，次のような演算表を考えると，単位元が0であることが容易に分かると思います．
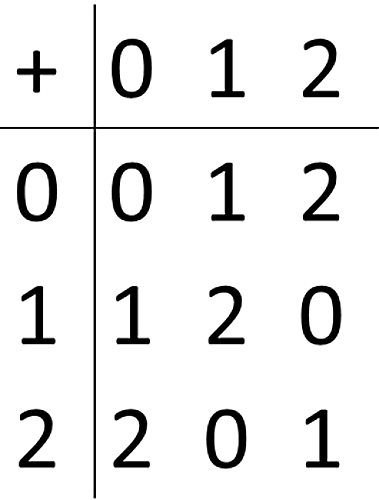演算表
ここで，定義から次の命題が得られます．
記号は定理のものと同じとする．
$\mathrm{Ker}(f)$は$X$の部分群で，$\mathrm{Im}(f)$は$Y$の部分群である．
部分群は，群になっている部分集合のことをいう．
これの証明はとりあえず省略します(たぶん今度書きます)．
定義ばかりで大変でしたがこれで準備は終わりです．では，主定理に行きましょう．
「空間は平面の積み重ね」を定式化する
本題にいきましょう．これには次の定理を使います：
$(X, +)$，$(Y, \times)$をそれぞれ群とし，$f:X\to Y$を準同型写像とする．このとき，$X/\mathrm{Ker}(f)\cong\mathrm{Im}(f)$が成り立つ．
これも証明は省略します(今度書きます)．
では，定式化しましょう．
$(\mathbb{R}^3, +)$，$(\mathbb{R}, +)$はそれぞれ群です．ここで，$f:\mathbb{R}^3\to\mathbb{R}$を，$f(x, y, z):=x+y+z$と定めます．ここで$f$は準同型です($\because f(x_1+x_2, y_1+y_2, z_1+z_2)=f(x_1, y_1, z_1)+f(x_2, y_2, z_2)$)．このとき，$\mathrm{Ker}(f)=\{(x, y, z)\in\mathbb{R}^3|x+y+z=0\}$，$\mathrm{Im}(f)=\mathbb{R}$です($\because$任意の$r\in\mathbb{R}$に対しても$(0, 0, r)\in\mathbb{R}^3, f(0, 0, r)=r$)．
ここで，$k\in\mathbb{R}$に対し，$S_k:=\{(x, y, z)\in\mathbb{R}^3|x+y+z=k\}$と定めましょう．すると，$(x_k, y_k, z_k)\in S_k$，$(x'_k, y'_k, z'_k)\in S_k$ならば，$(x_k-x'_k, y_k-y'_k, z_k-z'_k)\in\mathrm{Ker}(f)$です．よって$S_k$は同値類です．
以上より，準同型定理より，$\mathbb{R}^3/\mathrm{Ker}(f)\cong\{S_k|k\in\mathbb{R}\}$がいえます．このとき，$S_k$の自由度は$\mathbb{R}$だけになり，これは平面を表します．$\mathbb{R}^3/\mathrm{Ker}(f)$と$\{S_k|k\in\mathbb{R}\}$が群として同じであると主張しているので，これは「空間が平面の積み重ね」であることを示しています．
積み重ね
終わりに
目標だった定式化ができました．適当に書きすぎたので随時書き加えていきます．ここまで読んでくださってありがとうございます．
この記事を高評価した人
この記事に送られたバッジ
投稿者
