三角関数(逆三角関数)の図形的解法（はやい）
始
生命体のみなさんは, 日常生活において, 三角関数の中に逆三角関数が入った式, たとえばこういうのみたいなやつ:
$$
\sin(\arctan(x))=\frac{x}{\sqrt{1+x^2}}
$$
$$
\tan(\arcsec(x))=\sqrt{x^2-1}
$$
を展開する事が多々あると思います.
ふつうこれらを展開する場合には, 三角関数の相互関係からぐちゃぐちゃしていくのが一般的だと思いますが, 今回紹介する図形的な方法では, $\tan$や$\csc$などを含む全ての組み合わせに対して, それぞれ全く同じ手法でかつより素早く答えを導くことができます.
慣れれば5秒程度の暗算でもいけます.
早速手順を説明していきます.
手
$\sin(\arccos(x))$を開け.
手順1
まず, 三角関数の中に入っている逆三角関数部分に着目します.
$\sin(\arccos(x))$なら$\arccos(x)$です.
手順2
関数とその逆関数の合成関数はxになるので,
$$\cos(\arccos (x))=x$$
になります.
ここで, $\cos x$は直角三角形の隣辺を斜辺で割ったものといえるので,
$\cos(\arccos (x))=x$
からは,
隣辺が$a=x$, 斜辺が$h=1$の直角三角形が想定できます.
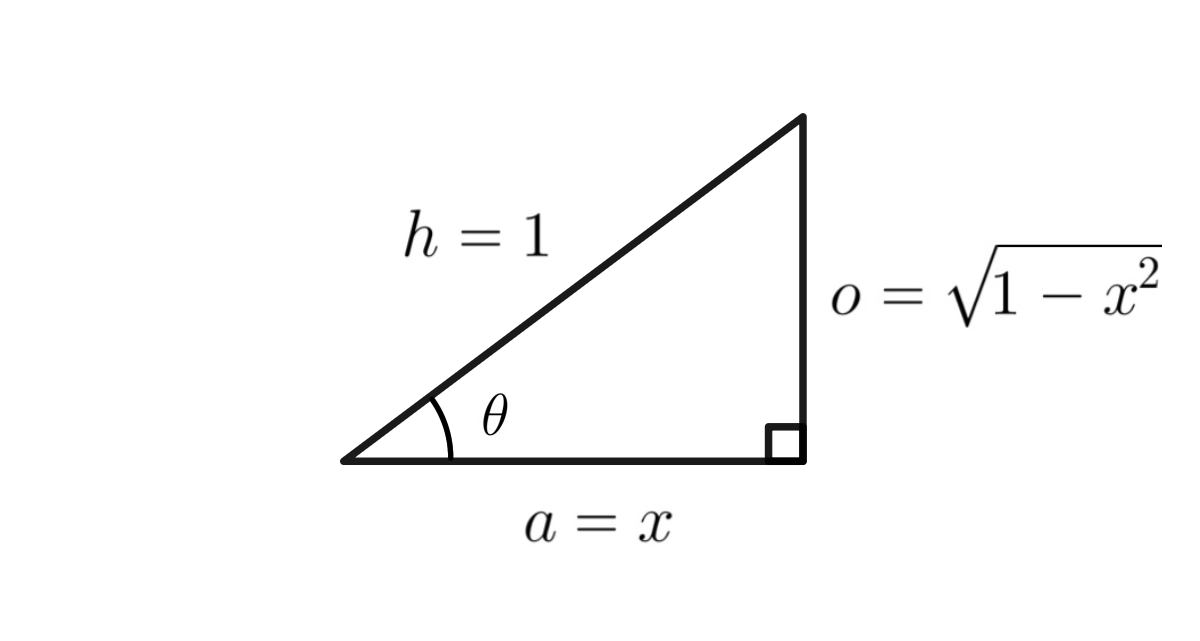こんなかんじ
（慣れないうちは紙に書いてみましょう）
手順3
三平方の定理（ピタゴラスの定理（鉤股弦の定理））より, 直角三角形の対辺は$o=\sqrt{1-x^2}$になります.
ここで, 求めたいのは$\sin(\arccos(x))$なので,
$\sin$, すなわち対辺を斜辺で割ったものを求めればよく, その$$\frac{o}{h}=\frac{\sqrt{1-x^2}}{1}= \sqrt{1-x^2}$$が求める$\sin(\arccos(x))$になります.
（範囲と符号に気をつけてね）
このくらいなら相互関係の方が早いかもですね.
他の例でもやってみましょう.
$\tan(\arcsin(x))$を開け.
$\tan(\arcsin(x))$で同じことをすると,
$\sin(\arcsin(x))=x$だから,
$o=x, h=1, a=\sqrt{1-x^2}$になります.
したがって, $\tan$は対辺を隣辺で割ったものなので,
$$\tan(\arcsin(x))=\frac{o}{a}=\frac{x}{\sqrt{1-x^2}}$$であることがわかります.
これがなぜ成り立つのかというと, そもそも逆三角関数が特定の条件をみたす直角三角形の角度であると見做せるからですね. まあ明らかではありますね.
応
では, 少し演習も3問ほどぶちかましてみましょう.
$\sin(\arccot(x))$を求めよ.
$$\Bigl(\cot x=\frac{1}{\tan x}\Bigr)$$
$\cot(\arccot(x))=x$で$\cot$は隣辺を対辺で割ったものだから, $a=x, o=1, h=\sqrt{1+x^2}$
よって,
$$\sin(\arccot(x))=\frac{o}{h}=\frac{1}{\sqrt{1+x^2}}$$
とまあこんな感じ.
$\dfrac{d}{dx} \arcsec(x)$ を求めよ.
$$\Bigl(\sec x=\frac{1}{\cos x}\Bigr)$$
$\arcsec(x)=y$とすると, $x=\sec y$.
よって$dx=\tan y \sec y \: dy$. すなわち$\dfrac{dx}{dy}=\tan y \sec y. $
したがって, $$\frac{d}{dx} \arcsec(x) = \frac{dy}{dx}
=\frac{1}{\frac{dx}{dy}}=\frac{1}{\tan y \sec y}=\frac{1}{\tan(\arcsec(x)) \sec(\arcsec(x))}$$
ここで
$\sec(\arcsec(x)=x$で,
$\tan(\arcsec(x))$は, $\sec$が$\dfrac{h}{a}$なので
$a=1, h=x, o=\sqrt{x^2-1}$より
$$\tan(\arcsec(x))=\frac{o}{a}= \sqrt{x^2-1}. $$
したがって,
$$\frac{d}{dx} \arcsec(x) = \frac{1}{x \sqrt{x^2-1}}$$
となります.
（範囲と符号に気をつけてね）
とまあこんな感じ.
$\tanh(\mathrm{arsinh}(x))$を求めよ.
考え方は同じです.
$\sinh(\mathrm{arsinh}(x))=x$で$\coth^2 x-\sinh^2 x=1$なので, 単位双曲線上でも円（三角関数）のときと同様に
$o=x, h=1, a=\sqrt{1+x^2}$と考えることができます.
したがって,
$$\tanh(\mathrm{arsinh}(x)) =\frac{o}{a}= \frac{x}{\sqrt{1+x^2}}$$
となります.
$\textcolor{lightgray}{SohCahToaとの相性が非常によい}$
あ、おわりです。