エルゴード理論で見る連分数展開の誤差極限
$a_0$は整数，それ以外の$a_n$は正の整数とするとき，
$$ x = a_0+\dfrac{1}{a_1+\dfrac{1}{a_2+\ddots}} $$
を正則連分数と呼びます．任意の実数$x$は，一意的に正則連分数へ展開できることが知られています．
では，連分数展開を途中で打ち切ったものと元の実数との誤差は，どの程度の大きさになるでしょうか．実は正則連分数展開の誤差について，その極限挙動を与える次の命題が知られています．
実数$x$の正則連分数展開を
$$ \displaystyle x = a_0+\dfrac{1}{a_1+\dfrac{1}{a_2+\ddots}}$$
としたとき，その第$n$次収束分数を
$$ \displaystyle x_n = a_0+\dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n}}}$$
とおく．このとき
$$\lim_{n \to \infty}\left| x - x_n \right|^{1/n} = \exp \left(-\frac{\pi^2}{6 \log 2} \right) \quad a.e.x \in \mathbb{R}$$
となる．
この命題については「ほとんど全ての実数」について成り立つという点に注意が必要です．実際，有理数や$\sqrt{2}$，さらには超越数である$e$などはいずれも例外になります．($\pi$で成り立つかどうかは，現在のところ未解決問題1です．)
それにしても$\exp \left(-\frac{\pi^2}{6 \log 2} \right)$とは何とも奇妙な値ですが，この記事ではなぜこの定数が現れるのかを解説していきます．
この命題はエルゴード理論を用いて証明出来ます．そこでまずは連分数の話は一旦置いて，エルゴード理論について軽く触れておきます．
エルゴード理論
エルゴード理論をざっくり説明すると，力学系を長時間観察したときの「時間平均」が，その力学系で取りうる状態全体の「空間平均（確率的な平均）」と，どのような条件で一致するかを記述し，そのような統計的性質を調べる理論です．
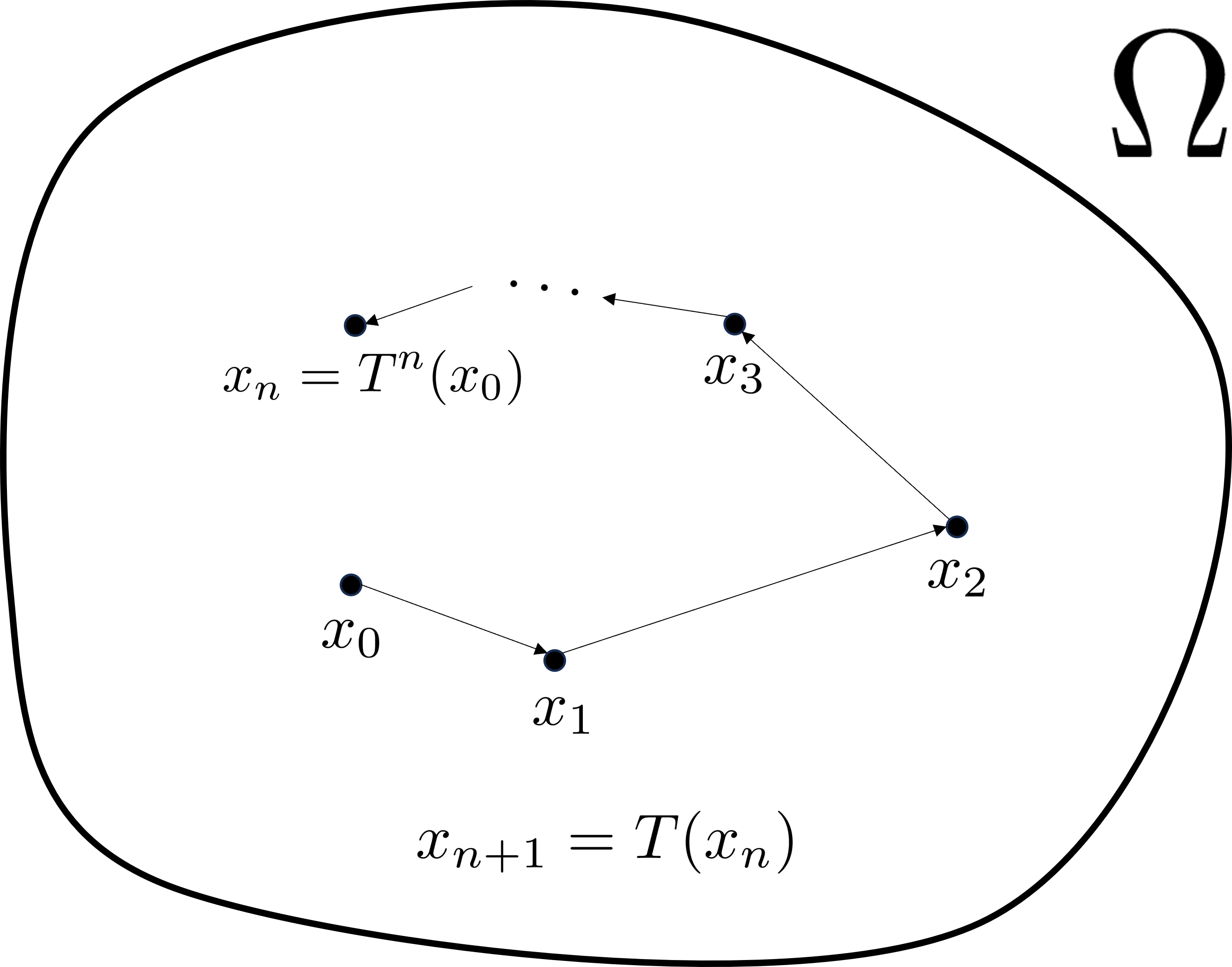
写像$T:\Omega \to \Omega$に対し，$x_0\in \Omega$を初期値として
$$ x_{n+1} = T(x_n)$$という離散的な力学系を考えましょう．軌道
$$ x_n = T^n(x_0), \quad n=0,1,\ldots $$
が空間$\Omega$の中に「まんべんなく」分布していると期待できるとき，その軌道に沿った量の時間平均と，$\Omega$全体に対する空間平均は一致しそうだと直感的には考えられます．この直感を数学的に正当化した概念がエルゴード性です．
確率空間$(\Omega, \mathcal{F}, \mu) $を考えます．可測写像$T: \Omega \to \Omega$が保測変換であるとは，任意の$A \in \mathcal{F} $に対して，$$ \mu \big(T^{-1}(A) \big) = \mu(A)$$が成り立つことを言います．このとき$(\Omega, \mathcal{F}, \mu, T) $を可測力学系と言います．
さらに，$A = T^{-1}(A) $を満たす任意の$A \in \mathcal{F}$に対して，
$$ \mu(A) = 0 ~\mbox{ or }~\mu(A) = 1$$
が成り立つとき，$(\Omega, \mathcal{F}, \mu, T) $をエルゴード的力学系と言います．
直感的にはこの「エルゴード的」という条件は，力学系が非自明な「閉じた集合」を持たないことを意味します．もし力学系がエルゴード的でないとすると，
$$ 0 <\mu(A)<1~\big(=\mu(\Omega) \big)$$であり，
$$ A=T^{-1}(A)$$を満たすような$A\in \mathcal{F}$が存在します．このとき，$A$の中から出発した力学系の軌道は永遠に$A$の中に閉じ込められ，空間全体をまんべんなく訪れることはありません．エルゴード性はこうした集合を（零集合は無視して）排除することで，(ほとんど全ての初期値に対して）力学系の軌道が（測度に比例した訪問頻度で）「まんべんなく分布する」振る舞いを保証していると理解できます．
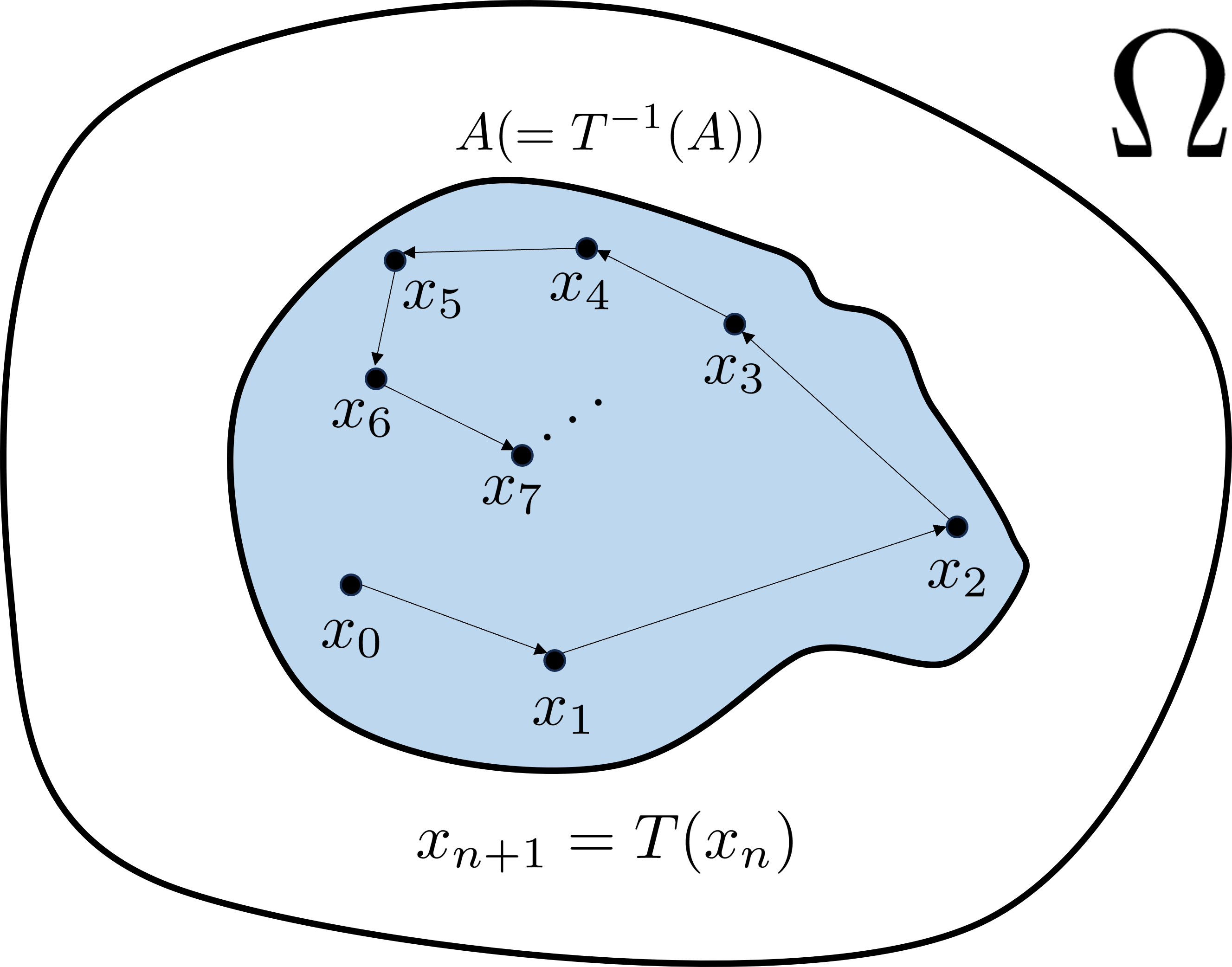エルゴード的ではない力学系のイメージ
ここで，エルゴード的力学系に対する時間平均と空間平均の関係を与える基本定理として，以下のバーコフのエルゴード定理を紹介します．
$(\Omega, \mathcal{F}, \mu , T)$を可測力学系とする．任意の$f\in L^1(\Omega, \mu)$に対して，ある$f^* \circ T = f^*$を満たす$f^* \in L^1(\Omega, \mu)$が存在して，
\begin{equation*}
\lim_{N\to \infty} \frac{1}{N} \sum_{k=0}^{N-1} f \big(T^k (x) \big) = f^*(x) \quad \mu \mbox{ - } a.e. x\in \Omega.
\end{equation*}が成り立つ．さらに，$(\Omega, \mathcal{F}, \mu , T)$がエルゴード的力学系ならば，
$$ f^*(x) = \int_\Omega f ~d\mu$$
となる．
この定理の証明は，例えば こちらのPDF を参照してください．
ガウス変換とガウス測度
ここでは，連分数とエルゴード理論を結びつけるためのガウス変換とガウス測度について紹介します．
連分数展開を力学的に（なにかの写像の繰り返しとして）捉えるにはどうすれば良いでしょうか．ここでは$x \in [0,1] \setminus \mathbb{Q}$としましょう．すると，整数部分は$0$であるため，
$$ x = \dfrac{1}{a_1+\dfrac{1}{a_2+\dfrac{1}{a_3+\ddots}}} $$
と正則連分数展開できます．両辺逆数を取ると，
$$ \frac{1}{x} = a_1+\dfrac{1}{a_2+\dfrac{1}{a_3+\ddots}} $$であり，$a_1$が$1/x$の整数部分，$ \dfrac{1}{a_2+\dfrac{1}{a_3+\ddots}}$が$1/x$の小数部分であるため，$\lfloor \cdot \rfloor$を床関数とすれば，
$$ \Big\lfloor \frac{1}{x} \Big\rfloor = a_1, \quad \frac{1}{x} - \Big\lfloor \frac{1}{x} \Big\rfloor = \dfrac{1}{a_2+\dfrac{1}{a_3+\ddots}}$$
となります．そこで，$\Omega := [0,1] \setminus \mathbb{Q}$として，$T: \Omega \to \Omega$を，
$$ T(x) := \frac{1}{x} - \Big\lfloor \frac{1}{x} \Big\rfloor$$と定義すれば，同じ操作をして，
$$ \Big\lfloor \frac{1}{T(x)} \Big\rfloor = a_2, \quad T \big(T(x) \big) = T^2(x)= \dfrac{1}{a_3+\ddots}$$
となります．したがってこれを繰り返すことで，
$$ \Big\lfloor \frac{1}{T^{n-1} (x)} \Big\rfloor = a_n, \quad T^n(x)= \dfrac{1}{a_{n+1}+\ddots}$$
が得られます．よって，$x$の連分数展開は
$$ x = \dfrac{1}{\Big\lfloor \frac{1}{T^0 (x)} \Big\rfloor+\dfrac{1}{\Big\lfloor \frac{1}{T^1 (x)} \Big\rfloor+\dfrac{1}{\Big\lfloor \frac{1}{T^2 (x)} \Big\rfloor+\ddots}}} $$
として記述することが出来ます．この写像$T$のことをガウス変換と呼びます．ここからエルゴード理論を展開するためには，まずはガウス変換が保測変換となるような$\Omega$上の確率測度が必要になります．実は$\mathcal{B}(\Omega)$を$\Omega$のボレル集合族としたとき，$A \in \mathcal{B}(\Omega)$に対して， 確率測度$\mu$を
$$ \mu(A) := \frac{1}{\log 2}\int_A \frac{dx}{x+1}$$
と定義すれば，ガウス変換は$\mu$の保測変換になります．実際，
$$\displaystyle I_k := \left(\frac{1}{k+1}, \frac{1}{k} \right]$$とおくと，$x \in I_k$のとき，
$$\displaystyle T(x) = \frac{1}{x} - k$$となるため，
\begin{align*}
\mu \big(T^{-1}(A) \big) &= \frac{1}{\log 2}\int_{T^{-1}(A)} \frac{dx}{x+1} \\
&= \frac{1}{\log 2} \sum_{k=1}^{\infty}\int_{T^{-1}(A)\cap I_k} \frac{dx}{x+1} \\
&= \frac{1}{\log 2} \sum_{k=1}^{\infty} \int_A \frac{1}{\frac{1}{y + k} + 1} \cdot \frac{1}{(y+k)^2} ~dy \\
&= \frac{1}{\log 2} \sum_{k=1}^{\infty} \int_A \left(\frac{1}{y + k} - \frac{1}{y+k+1} \right)~dy \\
&= \frac{1}{\log 2} \lim_{N \to \infty} \int_A \left(\frac{1}{y + 1} - \frac{1}{y+N+1} \right)~dy \\
&= \frac{1}{\log 2} \int_A \frac{1}{y+1} ~dy = \mu(A)
\end{align*}となり，確かに保測変換となることが成り立ちます．この確率測度$\mu$のことをガウス測度と呼びます．実はガウス測度はエルゴード的にもなるのですが，その証明は次のセクションに回します．
連分数の基本事項
ここでは連分数の基本事項をまとめます．
整数列$p_n$，正の整数列$q_n$を，$p_0=a_0$, $q_0=1$, 正の整数$n$に対して，
$$ \displaystyle a_0+\dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n}}} =: \frac{p_n}{q_n} \quad \big(\gcd(|p_n|, q_n) = 1 \big)$$
と置きます．二次正方行列
$$ M(a) := \begin{pmatrix} a & 1 \\ 1 & 0 \end{pmatrix} $$に対して，
$$ \displaystyle f_{M(a)}(x) :=a + \frac{1}{x} = \frac{ax + 1}{x} $$とおくと，$f_{M(a)}$は一次分数変換で，
$$\displaystyle f_{M(a)} \circ f_{M(b)} = f_{M(a)M(b)}$$が成立し，さらに$a, p$を整数, $q, x$を正の整数として$\gcd(|p|,q) = 1$ならば，
$$\displaystyle \frac{p}{q} = f_{M(a)}(x) \iff \begin{pmatrix} p \\ q \end{pmatrix}= M(a)\begin{pmatrix} x \\ 1 \end{pmatrix} $$
が成り立ちます．よって，
$$ \frac{p_n}{q_n} = f_{M(a_0)} \circ f_{M(a_1)} \circ \cdots f_{M(a_{n-1})} (a_n) $$
から，
$$ \begin{pmatrix} p_{n} \\ q_{n} \end{pmatrix}= M(a_0)M(a_1)\cdots M(a_{n-1})
\begin{pmatrix} a_{n} \\ 1 \end{pmatrix}$$
および
\begin{align*}
\begin{pmatrix} p_{n-1} \\ q_{n-1} \end{pmatrix} &= M(a_0)M(a_1)\cdots M(a_{n-2})
\begin{pmatrix} a_{n-1} \\ 1 \end{pmatrix} \\
&= M(a_0)M(a_1)\cdots M(a_{n-2})M(a_{n-1})\begin{pmatrix} 1 \\ 0 \end{pmatrix}
\end{align*}となります．したがって
$$ \begin{pmatrix} p_{n} & p_{n-1}\\ q_{n} & q_{n-1}\end{pmatrix}= M(a_0)M(a_1)\cdots M(a_{n})
\quad \ldots (1)$$
が成立します．よって，$ t \geq 0$に対して，
\begin{align*}
\displaystyle
&M(a_0)M(a_1)\cdots M(a_{n-1})
\begin{pmatrix} a_{n} + t \\ 1 \end{pmatrix} \\
& = M(a_0)M(a_1)\cdots M(a_{n})
\begin{pmatrix} 1 \\ t \end{pmatrix} \\
&= \begin{pmatrix} p_{n} & p_{n-1}\\ q_{n} & q_{n-1}\end{pmatrix} \begin{pmatrix} 1 \\ t \end{pmatrix} =\begin{pmatrix} p_n + p_{n-1} t \\ q_n + q_{n-1} t \end{pmatrix}
\end{align*}より，
$$ \displaystyle a_0 + \dfrac{1}{a_1+ \dfrac{1}{a_2+\ddots+\dfrac{1}{a_n + t}}} = \frac{p_n + p_{n-1} t}{q_n + q_{n-1} t} \quad \ldots (2)$$
が成り立ちます．また，$(1)$の両辺の行列式を求めることで，
$$ \displaystyle p_n q_{n-1} - p_{n-1} q_n = (-1)^{n+1} \quad \ldots (3)$$
が成り立ちます．これらの基本事項といくつかの補題を用いて，ガウス測度のエルゴード性を証明することが出来ます．しかし証明は少し長くなるのでツリー表示にしておきます．興味のある方はご覧ください．
証明を表示
位相空間$X$の部分集合族$\mathcal{C} \subset 2^X$が次を満たすとする:
任意の開集合$U \subset X$に対して，互いに素な（すなわち$i \neq j \Rightarrow I_i \cap I_j = \emptyset$が成り立つ）可算個の族$\left\{ I_k \right\}_{k=1}^{\infty} \subset \mathcal{C}$が存在し，
$$ \displaystyle U = \bigsqcup_{k=1}^{\infty} I_k$$
と表せる．
本記事では，このような性質をもつ集合族$\mathcal{C}$を被覆族と呼ぶことにする（この名称は本記事における便宜的な用語であり，おそらく一般的な呼び方ではない）．
まず，被覆族と正則な確率測度に関する以下の補題を証明する．
補題1
確率位相空間$(\Omega, \mathcal{F}, \mu)$で，$\mu$を正則な確率測度とする．このとき，
$A \in \mathcal{F}$および$\Omega$の被覆族$\mathcal{C} \subset \mathcal{F}$に対して，ある$\lambda > 0$が存在して，任意の$I \in \mathcal{C}$に対して，
$$ \mu(I \cap A) \geq \lambda \mu(I)$$を満たすとき，$\mu(A) = 1$となる．
$\because$ 被覆族の条件から，任意の開集合$U \subset \Omega$に対して，ある$\{I_k\}_{k=1}^{\infty} \subset \mathcal{C}$が存在して，
$$ \displaystyle U = \bigsqcup_{k=1}^{\infty} I_k$$となるため，
$$ \displaystyle \mu(U \cap A) = \sum_{k=1}^{\infty} \mu(I_k \cap A) \geq \sum_{k=1}^{\infty} \lambda \mu(I_k) = \lambda \mu(U)$$となる．ここで，$\mu$は正則より，任意の$\varepsilon > 0$に対して，ある開集合$V \supset A^c$が存在して，$\mu(V \setminus A^c) < \varepsilon$となる．したがって，
\begin{align*} \varepsilon > \mu(V \setminus A^c) = \mu(V \cap A) \geq \lambda \mu(V) \geq \lambda \mu(A^c) \end{align*}より，$\varepsilon \downarrow 0$とすれば，$\mu(A^c) = 0$より，$\mu(A)=1$となる． $\square$
さらに次の補題を証明する．
補題2
$\Omega := [0,1] \setminus \mathbb{Q}$に$\mathbb{R}$からの相対位相を入れる．
$T:\Omega \to \Omega$をガウス変換，$x \in \Omega$および正の整数$n$に対して， $$ a_n(x) := \Big\lfloor \frac{1}{T^{n-1} (x)} \Big\rfloor$$すなわち
$$ x = \dfrac{1}{a_1(x)+\dfrac{1}{a_2(x)+ \ddots }}$$と連分数展開されるものとする．このとき
$$ I(a_1, \ldots ,a_n) := \left\{x \in \Omega \mid a_1(x) = a_1, \ldots , a_n(x) = a_n \right\} $$とおけば，集合族$$ \mathcal{C}:= \left\{I(a_1, \ldots ,a_n) \mid n \in \mathbb{N}, ~a_n \in \mathbb{N} \right\}$$は$\Omega$の被覆族である．
$\because$ $I(a_1, \ldots ,a_n)$は
$$ \displaystyle \dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n}}} ~\mbox{と}~ \dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n+1}}}$$を端点に持つ区間（$\setminus \mathbb{Q}$）となる．連分数展開の一意性から，
$$ I(a_1, \ldots ,a_n) \cap I(b_1, \ldots ,b_m)\neq \emptyset$$ならば，必ず
$$ I(a_1, \ldots ,a_n) \subset I(b_1, \ldots ,b_m) ~\mbox{または}~I(a_1, \ldots ,a_n) \supset I(b_1, \ldots ,b_m)$$のどちらかが成立する．そこで
$$ I_n(x) := I(a_1(x),\ldots, a_n(x)) $$とすると，
$$ \displaystyle I_1(x) \supset I_2(x) \supset \cdots \supset \bigcap_{n \in \mathbb{N}} I_n(x) = \{x\}$$より，任意の$(a,b) \subset [0,1]$および任意の$x \in (a,b) \setminus \mathbb{Q}$に対して，ある自然数$n$が存在して，$I_n(x) \subset (a,b) \setminus \mathbb{Q}$となる．そこで，
$$ n(x) := \min \left\{n \in \mathbb{N} \mid I_n(x) \subset (a,b) \setminus \mathbb{Q} \right\}$$と定め，
$$ J(x) :=I_{n(x)}(x) \subset (a,b) \setminus \mathbb{Q}$$とおく．先ほどの包含関係の性質と$n(x)$の最小性から，$$ J(x) \cap J(y) \neq \emptyset \Rightarrow J(x) = J(y)$$が従う．したがって，
$$ \mathcal{J}:= \left\{J \big(x \big) \mid x \in (a,b) \setminus \mathbb{Q} \right\}\subset \mathcal{C}$$は互いに素な高々可算個の族であり，
$$ \displaystyle \bigsqcup_{J \in \mathcal{J}} J = (a,b) \setminus \mathbb{Q}$$となる．よって$\mathbb{R}$の任意の開集合は互いに素な高々可算個の開区間の和で表せるため，$\mathcal{C}$は被覆族．$\square$
さらに，この被覆族$\mathcal{C}$およびガウス測度$\mu$に対する以下の補題を証明する．
補題3
ある定数$\gamma > 0$が存在して，任意の$I_n = I(a_1, \ldots , a_n) \in \mathcal{C}$および任意の開集合$U \subset \Omega$に対して，
$$ \displaystyle \mu \big(T^{-n}(U) \cap I_n \big) \geq \gamma \mu (U) \mu(I_n)$$
となる．
$\because$ 以下では，正の定数の違いを無視するために，ある定数 $C>0$ が存在して
$$ A \leq C B,\quad A \geq C B $$
が成り立つことをそれぞれ
$$ A \lesssim B,\quad A \gtrsim B $$と表すことにする．また，便宜上，開区間 $(a,b)$ と $(a,b)\setminus \mathbb{Q}$ を同一視する．$\mathbb{R}$の任意の開集合は互いに素な高々可算個の開区間の和で表せることに注意すれば，任意の$0 < a < b < 1$に対して，
$$ \displaystyle \mu \big(T^{-n}(a, b) \cap I_n \big) \gtrsim \mu (a,b) \cdot \mu(I_n)$$を示せば十分である．$\mathcal{L}^1$を$1$次元ルベーグ測度とすれば，任意の$A \in \mathcal{B}(\Omega)$に対して，
$$ \frac{1}{2\log 2} \mathcal{L}^1(A)\leq \mu(A) \leq \frac{1}{\log 2} \mathcal{L}^1(A)$$より，ガウス測度と$1$次元ルベーグ測度は同値．
$x \in T^{-n}(a,b) \cap I_n$とすると，$T^n (x) \in(a,b)$であり，$$ x = \cfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n + T^n (x)}}} $$に注意すれば，$T^{-n}(a,b) \cap I_n$は
$$ \displaystyle \dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n + a}}} ~\mbox{と}~ \dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n + b}}} $$を端点に持つ区間であることが分かるので，$(2)$より，$$ \mathcal{L}^1\bigl(T^{-n}(a,b) \cap I_n\bigr) = \left|\frac{p_n + p_{n-1} b}{q_n + q_{n-1} b} -\frac{p_n + p_{n-1} a}{q_n + q_{n-1} a}\right|. $$したがって，$\mu$と$\mathcal{L}^1$の同値性より，
\begin{align*} \displaystyle &\mu \big(T^{-n}(a,b) \cap I_n \big) \gtrsim \mathcal{L}^1 \big(T^{-n}(a,b) \cap I_n \big) =\left|\frac{p_n + p_{n-1} b}{q_n + q_{n-1} b} - \frac{p_n + p_{n-1} a}{q_n + q_{n-1} a}\right| \end{align*}が得られる．また$(3)$から，$|p_n q_{n-1} - p_{n-1} q_{n}| = 1$が成り立つので，
\begin{align*} \displaystyle \left|\frac{p_n + p_{n-1} b}{q_n + q_{n-1} b} - \frac{p_n + p_{n-1} a}{q_n + q_{n-1} a}\right| &=\left| \frac{(a-b)(p_n q_{n-1} - p_{n-1} q_{n})}{(q_n + q_{n-1} b)(q_n + q_{n-1} a)}\right| \\ &= \mathcal{L}^1(a,b) \left| \frac{1}{(q_n + q_{n-1} b)(q_n + q_{n-1} a)}\right| \end{align*}
となる．さらに，
$$ \mathcal{L}^1(I_n) = \left| \frac{1}{q_n(q_n + q_{n-1})}\right| $$であるから，これを用いて
$$ \displaystyle \left|\frac{p_n + p_{n-1} b}{q_n + q_{n-1} b} -\frac{p_n + p_{n-1} a}{q_n + q_{n-1} a}\right| = \mathcal{L}^1(a,b)\, \mathcal{L}^1(I_n) \left|\frac{q_n(q_n + q_{n-1})} {(q_n + q_{n-1} b)(q_n + q_{n-1} a)}\right|$$と書ける．また，$0 < a,b < 1 $,$q_{n-1} < q_n$に注意して，
$$ \left| \frac{q_n(q_n + q_{n-1})}{(q_n + q_{n-1} b)(q_n + q_{n-1} a)}\right| \geq \left| \frac{q_n (q_n + q_{n-1})}{(q_n + q_n)(q_n + q_{n-1})}\right| = \frac{1}{2}$$が従う．したがって，
$$ \displaystyle \mu \big(T^{-n}(a,b) \cap I_n \big) \gtrsim \mathcal{L}^1(a,b) \mathcal{L}^1(I_n) \gtrsim \mu(a,b) \mu(I_n)$$ が得られる．$\quad \square$
それではこれらの補題を使って，ガウス測度がエルゴード的になることの証明をしましょう．
$A = T^{-1}(A)$を満たす$A \in \mathcal{B}(\Omega)$に対して，$\mu(A) > 0$を仮定する．
先に述べた通り，$1$次元ルベーグ測度とガウス測度は同値であるため，ガウス測度も正則である．したがって，任意の$\varepsilon > 0$に対して，ある開集合$U$が存在して，$U \supset A$かつ$\mu(U \setminus A) < \varepsilon $を満たす．さらに，$T$は保測変換であるため，
$$ \mu \big(T^{-n} (U \setminus A) \big) = \mu(U \setminus A) < \varepsilon$$も成立する．したがって，任意の$I=I(a_1, \ldots , a_n) \in \mathcal{C}$に対して，
$$ \mu(A \cap I ) + \varepsilon > \mu \big(T^{-n} (U) \cap I \big) $$となる．また，補題3 より，ある$\gamma > 0$が存在して，
$$ \mu \big(T^{-n} (U) \cap I \big) \geq \gamma \mu(U) \mu(I) \geq \gamma \mu(A) \mu(I)$$から，
$$ \mu(A \cap I ) + \varepsilon \geq \gamma \mu(A) \mu(I)$$
となる．よって，$\varepsilon \downarrow 0$とすれば，
$$ \mu(A \cap I ) \geq \gamma \mu(A) \mu(I)$$が得られて，$\lambda :=\gamma \mu(A) >0 $とすれば，補題1 より$\mu(A)=1$となる．$\square$
命題の証明
それでは，ここまでの準備のもとで，最初に紹介した命題を証明していきましょう．
整数部分の打ち消しから，$\Omega := [0,1]\setminus \mathbb{Q}$として，$x \in \Omega$の場合だけを考えれば十分である．以下$T$をガウス変換，$\mu$をガウス測度とする．
$$ x = \dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots}} $$とおくと，「連分数の基本事項」セクションの$(2)$より，正の整数$n$に対して，
\begin{equation*}
x = \dfrac{1}{a_1+\dfrac{1}{a_2 +\ddots+\dfrac{1}{a_n + T^n (x)}}} = \frac{p_n + p_{n-1}T^n (x)}{q_n + q_{n-1} T^n (x)}
\end{equation*}が成立する．これを$T^n (x)$について解くと，
$$ \displaystyle T^n (x)= -\frac{x q_n - p_n}{x q_{n-1} - p_{n-1}}$$
となるため，正の整数$N$に対して，
\begin{align*}
\prod_{k=0}^{N-1} T^k (x) &=(-1)^{N} \cdot x \cdot\frac{x q_1 - p_1}{x} \cdot \frac{x q_2 - p_2}{x q_1 - p_1} \cdot \ldots\cdot \frac{x q_{N-1} - p_{N-1}}{x q_{N-2} - p_{N-2}} \\
&= (-1)^N (xq_{N-1} - p_{N-1}) \\
&= |xq_{N-1} - p_{N-1}|
\end{align*}となる．ここで，$|xq_{N-1} - p_{N-1}|$の$x$に，
$$ x = \frac{p_N + p_{N-1}T^N (x)}{q_N + q_{N-1} T^N (x)}$$
を代入すれば，「連分数の基本事項」セクションの$(3)$より，$|p_N q_{N-1} - p_{N-1} q_{N}| = 1$に注意して，
\begin{equation}
|xq_{N-1} - p_{N-1}| = \frac{1}{q_{N} + q_{N-1} T^N (x)}
\end{equation}となる．また，$q_{N-1} \leq q_N$, $0 < T^N (x) < 1$に注意すれば，
\begin{equation}
\frac{1}{2 q_N} \leq \frac{1}{q_{N} + q_{N-1} T^N (x)} \leq \frac{1}{q_N}\quad \ldots(*)
\end{equation}を満たす．よって，
\begin{equation*}
\frac{1}{2q_N} \leq \prod_{k=0}^{N-1} T^k (x) \leq \frac{1}{q_N}
\end{equation*}が成り立つ．両辺対数を取り，$N$で割った極限を考えると，バーコフのエルゴード定理から，
\begin{align*}
&-\lim_{N \to \infty} \frac{1}{N}\log q_N \\
&= \lim_{N \to \infty}\frac{1}{N} \sum_{k=0}^{N-1} \log \left(T^k (x) \right) \\
&= \int_{\Omega} \log x ~d\mu\\
&= \frac{1}{\log 2} \int_{0}^1 \frac{\log x}{1+x} ~dx=-\frac{\pi^2}{12 \log 2} \quad a.e.x \in \Omega
\end{align*}が成立する．（ガウス測度と$1$次元ルベーグ測度の同値性から，$\mu \mbox{ - } a.e.x \in \Omega$でも$\mathcal{L}^1\mbox{ - }a.e.x \in \Omega$でも良いことに注意．）
(最後の積分の計算方法は以下のツリーを参照してください．)
計算方法を表示
\begin{align*} \int_{0}^1 \frac{\log x}{1+x} ~dx &= \int_{0}^1 \sum_{k=0}^{\infty} (-1)^{k} x^k \log x ~dx \end{align*}について，\begin{align*} f_N(x) := \sum_{k=0}^{N} (-1)^{k} x^k \log x \end{align*}とおく．$x \in (0,1)$のとき，
\begin{align*} |f_N(x)| &\leq \sum_{k=0}^{N} x^k |\log x| \\ &\leq \frac{|\log x|}{1-x} \\ &= \frac{-\log x}{1-x} =: g(x) \end{align*}
とすると，
\begin{align*} \int_{0}^1 g(x)~dx &= \int_0^{1/2} g(x) ~dx + \int_{1/2}^1 g(x) ~dx \\ &\leq \int_0^{1/2} \frac{-\log x}{1 - 1/2} ~dx + \int_{1/2}^1 \frac{-\log(1/ 2)}{1 - 1/2} ~dx \\ &= \frac{1}{2} (1 + 3 \log 2) < \infty \end{align*}より，$g$は可積分．したがってルベーグの優収束定理より，
\begin{align*} \int_{0}^1 \frac{\log x}{1+x} ~dx &= \int_{0}^1 \sum_{k=0}^{\infty} (-1)^{k} x^k \log x ~dx \\ &= \int_{0}^1 \lim_{N \to \infty }f_N(x) ~dx\\ &= \lim_{N \to \infty }\int_{0}^1 f_N(x) ~dx\\ &= \sum_{k=0}^{\infty}(-1)^{k} \int_{0}^1 x^k \log x ~dx \\ &= -\sum_{k=0}^{\infty} \frac{(-1)^{k}}{(k+1)^2} = -\frac{\pi^2}{12}. \end{align*}
したがって，
\begin{equation*} \lim_{N \to \infty} q_N^{1/N} = \exp(\frac{\pi^2}{12 \log 2}) \quad a.e. x \in \Omega \end{equation*}が成立する．また，$(*)$から，
\begin{equation} \frac{1}{2q_N q_{N+1} } \leq \left|x - \frac{p_N}{q_N} \right| \leq \frac{1}{q_N q_{N+1}} \end{equation}となるため，
\begin{equation} \lim_{N \to \infty} \left|x - \frac{p_N}{q_N} \right|^{1/N} =\lim_{N \to \infty} \left(q_N^{1/N} \right)^{-2} = \exp \left(-\frac{\pi^2}{6 \log 2} \right) \quad a.e. x \in \Omega \end{equation}が得られる．$\quad \square$
まとめ
この命題は，ほとんど全ての実数$x$に対して，連分数による第$n$次収束分数$p_n / q_n$との誤差の対数が
$$ \displaystyle \log \left|x - \frac{p_n}{q_n} \right| \sim -\frac{\pi^2}{6 \log 2} n $$
を満たすことを意味しており，連分数の誤差の振る舞いが，エルゴード理論を通じて一つの具体的な定数として現れることを示しています．
エルゴード理論を用いて連分数展開を調べると，他にも
ヒンチンの定数
など，面白い話題が色々知られています．興味があれば是非調べてみてください．
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
