オイラー関数の繰り返し周辺

　いまから，55年前の高2の時に気づいたオイラー関数の(日本ではあまり知られていない)或る性質とその周辺を紹介することを目的としています．
　オイラー関数 $\varphi$ では$n>1$について$\varphi(n)\lt n$が成り立っていることから，
$$ \begin{align*} \varphi(\varphi(n)),~\varphi(\varphi(\varphi(n))),\cdots ,~\varphi(\varphi(\cdots (\varphi(n))\cdots )) \end{align*} $$
とオイラー関数を繰り返して作用させてゆくと，いつかは$1$にたどり着くことがわかります．

つまり，$\varphi^{k}(n)=\varphi(\varphi^{k-1}(n)),(k\geqq 2),\quad \varphi^{1}(n)=\varphi(n)$と書くことにすれば，どのような$n$についても，ある($n$に依存する)$k=k(n)$で初めて$\varphi^{k}(n)=1$となることがわかります．
$$ \begin{align*} \varphi(2)&=1 \\ \varphi(3)&=2,~\varphi(2)=1 \qquad \varphi(\varphi(3))=\varphi^2(3)=1 \\ \varphi(4)&=2,~\varphi(2)=1 \qquad \varphi(\varphi(4))=\varphi^2(4)=1 \\ \varphi(5)&=4,~\varphi(4)=2,~\varphi(2)=1 \qquad \varphi(\varphi(\varphi(5)))=\varphi^3(5)=1 \\ \varphi(6)&=2,~\varphi(2)=1 \qquad \varphi(\varphi(6))=\varphi^2(6)=1 \\ &\cdots \cdots \\ \varphi(100)&=40,~\varphi(40)=16,~\varphi(16)=8,~...,~\varphi^6(100)=1 \\ &\cdots \cdots \end{align*} $$
という具合です．

　では，何回で$1$にたどり着くのか，その回数$k(n)$を計算してみましょう．

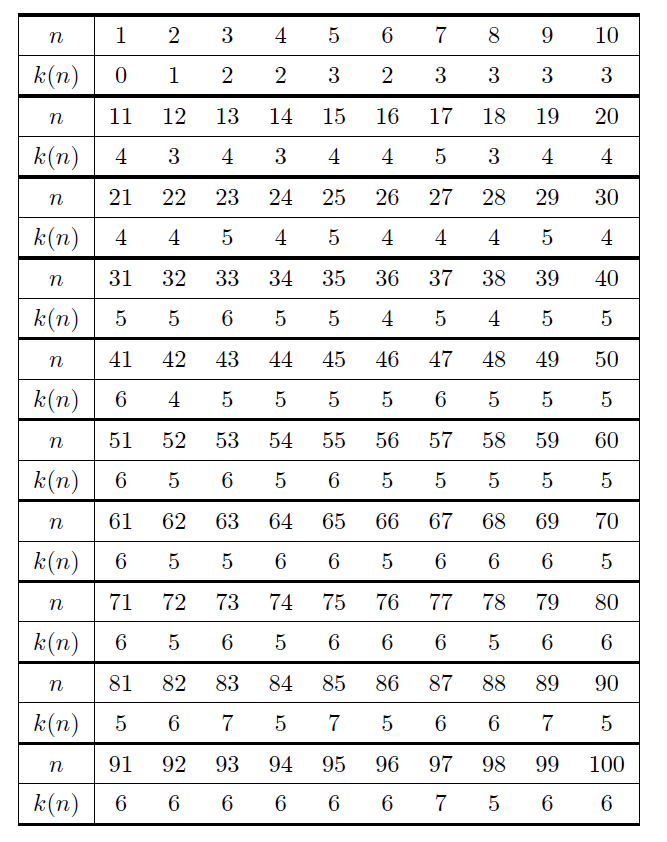何回でたどり着く
　この$k=k(n)$についての性質をインドの数学者・ヴァイディアナタスワミ(R. Vaidyanathaswami)から提起された問題として初めて調べたのが，インドの数学者ピライ(S. S. Pillai)でした．（S. S. Pillai,ON A FUNCTION CONNECTED WITH $\varphi(n)$, Bull. Amer. Math. Soc. $\bf 35$(1929), 837-841；S. S. Pillai, On an arithmetic function, Annamalai University Journal, ${\bf 2}$, (1933), 242-248）

　ピライは$n$についての$k$を$R(n)$として，その簡単な評価式
$$ \begin{align*}\label{PR} \left[ \dfrac{\log n}{\log 2} \right]\geqq R(n)-1\geqq \left[ \dfrac{\log \dfrac{n}{2}}{\log 3} \right] \tag{PR} \end{align*} $$
を導きましたが，以下のような関係式については$n=2^s,~n=2^s\cdot 3^t$の特殊な場合にしか言及できませんでした．

　その14年後，アメリカの数学者シャピロ(H.N.Shapiro，当時Princeton大)が $n$ についての $k$ を$C(n)$, $C(1)=0$とし，自然数 $x,~y$ として，ほぼ対数的な次のような厳密な関係を導き出しました．（H. Shapiro, AN ARITHMETIC FUNCTION ARISING FROM THE $\phi$ FUNCTION, Amer. Math. Monthly ${\bf 50}$ (1943), 18-30）この時点では，シャピロはピライの仕事を知らなかったようです．というのは，このShapiroの論文では，参照文献の記載もなく，Pillaiの結果には触れられていなかったからです．
$$ \begin{align*} C(xy)=\left\{ \begin{array}{ll} C(x)+C(y) & (\ x\ \mbox{ もしくは }\ y\ \mbox{ が奇数 }\ ) \\ C(x)+C(y)+1 & (\ x\ \mbox{ と }\ y\ \mbox{ が偶数 }\ ) \end{array} \right. \tag{SC} \end{align*} $$
　このオイラー関数の繰り返し問題については，シャピロ以降，(シャピロの結果を知らずに結果を得られていたオーストラリアの)バーンズ（E. S. Barnes., Note 225, Australian Math. Teacher ${\bf 11}$ (1955), 20-21）とリンドグレン（H. Lindren, Australian Math. Teacher ${\bf 11}$ (1955), 52-53）以外，実に多くの数学者が様々な形で扱っています．（1960年代では，アラダル（M. Aladar, Az Euler-fél $\phi$ -függvény iterálsával nyert számelméleti függvényröl, Mat. Lapok (Budapest) ${\bf 11}$ (1960), 46-67），パルナミ（J. C. Parnami, On iterates of Euler's $\phi-$function, Amer, Math. Monthly, ${\bf 74}$ (1967), 967-968.）等が知られています）。また，この頃，エルデシュ(P. Erdös)，ポメランス(C. Pomerance)，スッバラオ(M.V. Subbarao)等多くの数論学者が数論的関数のiteration問題を扱っています．

　シャピロが導いた$C(x)$に関する公式は，完全対数的になっていないところが少しばかり残念ではありますが，整数$n$が$\varphi$によって$1$にたどり着く最小回数としては正確に表しているものになります．

　一方，バーンズは$n$に対する最小の$s=s(n)$として$\varphi^s(n)=1$であるとき，$I(1)=0$とした上で
$$ \begin{align*} I(n)=\left\{ \begin{array}{ll} s & n\mbox{ が偶数 } \\ s-1 & n\mbox{ が奇数 } \end{array} \right. \end{align*} $$
　を示し，対数的であることを示しましたが，発表後シャピロの結果を知ったと，先の発表物の中での中で述べていました．

　ここで$L(n)$を次のように決めておくと
$$ \begin{align*} L(n)=\left\{ \begin{array}{ll} L(\varphi(n)) +1 & (n \mbox{が偶数のとき}) \\ L(\varphi(n)) & (n \mbox{が奇数のとき}) \end{array} \right. \end{align*} $$
すると，このとき　すべての自然数$x,~y$について
$$ \begin{align*} L(xy)=L(x)+L(y) \end{align*} $$
が成立し，$L$が完全対数的(加法的)であることが導かれます．このことは，バーンズやリンドグレンも指摘していました．

　山下が高2のときに気づいた関係式が，この$L$でした．

　個人的には，シャピロのように偶奇によって半対数的関係式を示すより$L$のように全整数で完全対数的な関係式で示す方が便利だと思えます．$1$にたどり着く回数が気になるときは，$n$が奇数のときだけ，$L(n)$に$1$を加える作業で済むからです．計算上は$L$のまま扱っておくほうが便利なのではないでしょうか．
　大学入学後。様々な初等整数論の成書を開いても，(ボクにとって)面白いこの事実は紹介されていませんでした．また何人かの先生に聞いても反応はなく，思い切って，M1のときに（B2のときにUBC@ICM1974で面識のあった）内山三郎先生（当時，岡山大）に問うて，初めてこの性質の一連の流れについて知った次第です．

　山下は，大学入学時から(当時，秋月－永田の"近代代数学"で導来正規環の学習をしていて，"導来"という言葉を気に入り)勝手にオイラー関数の導来対数関数と呼称していました．

　シャピロは1950年に自身の結果をさらに拡張して（H. Shapiro, On the iterates of certain class of arithmetic functions, Comm. Pure Applied Mth. ${\bf 3}$ (1950), 259-272），$f,\ A$を自然数値をもつ数論的関数で，$f(p_{i})$を素数$p_{i}$については$1\leqq f(p_{i})< p_{i}$，$A$は奇素数$p_{i}$については$A(2)=2,\ 2\lt A(p_{i})\leqq p_{i}$として

$$ \begin{align*} f(n)=\prod_{i=1}^{r}f(p_{i})\left( A(p_{i} \right)^{e_{i}-1} \end{align*} $$

とし，$f(n)\lt n$ であることから，$n\gt 2$について，ある$k=k_{f}(n)$について，
$$ f^{k}(n)=2 $$
であることから，$k_f(1)=k_f(2)=0$として
$$ c_{f}(n)=\left\{ \begin{array}{ll} k_f(n) & n:\mbox{odd} \\ k_f(m)+1 & n:\mbox{even} \end{array} \right. $$
を定義し，先の$C(n)$と同様の関係式を有することを示しました．

　一方，宮田－山下は別視点で次のことを示しました．（2004.9 日本数学会秋季総合分科会・応用数学分科会）

　各素数$p$について，$f$ を$1\leq f(p)\lt p$であるような関数とし，$\varphi_{f}$を
$$ \begin{align*} \varphi_{f}(n)=n\prod_{i=1}^{s}\dfrac{f(p_i)}{p_i} \qquad (n=\prod_{i=1}^{s}p_{i}^{e_{i}}) \end{align*} $$
と定め，
$$ \begin{align*} L_{\varphi_{f}}(n)=\left\{ \begin{array}{ll} 0 & n=1 \\ L(\varphi_{f}(n))+\#\left|\{ p\in f^{-1}(1):p|n \}\right| & n\gt 1 \end{array} \right. \end{align*} $$
と定義すれば
$$ \begin{align*} L_{\varphi_{f}}(xy)=L_{\varphi_{f}}(x)+L_{\varphi_{f}}(y) \end{align*} $$
が導かれます．

　証明の方針は，$x=\displaystyle\prod_{i=1}^{s}p_{i}^{e_{i}}$ の帰納法によります．$x$ 未満では成立しているものとしておきます．

$$ L_{\varphi_{f}}(x)=e_{1}L_{\varphi_{f}}(p_{1})+e_{2}L_{\varphi_{f}}(p_{2})+\cdots+e_{s}L_{\varphi_{f}}(p_{s})=\sum_{i=1}^{s}e_{i}L_{\varphi_{f}}(p_{i}) $$
を示せば十分です．

　$\alpha=\#|\{ p\in f^{-1}(1) : p|x \}$ として，素数 $p$ に対して，$f(p)=1$ なら $L_{\varphi_{f}}(f(p))=0$，そうでなければ $L_{\varphi_{f}}(f(p))=L_{\varphi_{f}}(p)$ であることに注意して
$$ \begin{align*} L_{\varphi_{f}}(x)&=L_{\varphi_{f}}(\varphi(x))+\alpha \\ &=\sum_{i=1}^{s}(e_{i}-1)L_{\varphi_{f}}(p_{i})+\sum_{i=1}^{s}L_{\varphi_{f}}(f(p_{i}))+\alpha \\ &=\sum_{i=1}^{s}(e_{i}-1)L_{\varphi_{f}}(p_{i})+\sum_{i=1}^{s}L_{\varphi_{f}}(p_{i})-\alpha+\alpha \\ &=\sum_{i=1}^{s}e_{i}L_{\varphi_{f}}(p_{i}) \end{align*} $$
　ここでの $\alpha=0,1$ が $L(x)$ での $x$ の扱い，奇偶の扱いに対応していて，$L(x)$ に関する対数関係式の別証を与えています．