お前も物理学徒にならないか？

はじめに

挨拶

　こんにちは, うどんです. この記事はPhysics Lab. Advent Calendar2026, シリーズ2の12日目への寄稿です.

　東京大学理学部物理学科の学生の生態に対してどのようなイメージを抱いているでしょうか？physlab2026アドベントカレンダーをみたことある人なら, どうせ夜中の1時から4時に勉強してそこから寝て, 9時くらいに起きて授業2限だけなんだろう... そんなことを思っていらっしゃるかもしれませんね.
　はっきり言います, そんなことはありません！ほぼ隔週で実験を昼から夕方にかけて行い, 実験がない時もレポートに追われているのです. そんな私たちですが, 合間を縫って仲間たちと自主ゼミを行い, 日々強い物理学徒になるため精進しています.

強い物理学徒

　ところで強い物理学徒とは何でしょうか？
\begin{align} 1. &\; \text{物理に関する知見が広い} \\ 2. &\; \text{物理学実験での解析に穴がない} \\ 3. &\; \text{物理の問題を解くのが早い} \\ 4. &\; \text{強い力で相互作用する} \end{align}
などなどです. 特に4番のせいで常に理学部一号館に閉じ込められている人もいます.

　私が思うに物理学科には物理できる人は多いです. ゆえに物理以外にも強いと相手に思わせられるようなものが必要です. どんなものがあげられるでしょうか？

　まずは人間として強くなることを考えます. 筋トレや運動, 生活習慣を正すなど色々な方法がありますが, 環境に負けない強さを求めることを今回は考えていきます.

生物として

　突然ですか, 皆さんはこの季節にどんな服装をしているでしょうか？ 今月は12月, 気温は最高気温でさえ10度前後, クリスマス頃になればもっと冷え込むことでしょう. 多くの方が長袖を纏い, ダウンやコートを身につけているかと思います.

　そんな中, タンクトップに半ズボン, サングラスの人間が目の前を通りかかったら, どのような感情を抱くでしょうか？

タンクトップ, 半ズボンで歩く人

\begin{align} \textcolor{red}{俺(私)はあの人には勝てない. この季節にあの格好は生物として負けた... 強すぎる} \end{align}
　皆さんそう思うことでしょう. 私が思う強い物理学徒とはこのような人間のことを指します.

強くなるために

　そうと聞けば早速その格好になって生活しよう！そう思ったのも束の間, 皆さんは気づくと思います. この季節どこの店行ってもタンクトップなんて売ってないんじゃないか... そうですね, 夏ならまだしも, 今は冬ですもんね. そんなもの近くのお店にはないと思います.
　ではどうすればいいか. 簡単です. 長袖をハサミで切ったらいいんですよ. 一件落着ですね.

長袖をハサミで切る！！

　ところがどっこい. ある人がいいました. そんなことしたら, 布がほつれちゃうじゃないかと.

ほつれた元長袖

　あっ確かに, どうしよう... いや待てよ, 安直に考えたら布がほつれて境界面がギザギザしそうだけど, 本当にそう見えるのかな？ここで物理学徒の悪いところが出てしまいました. こういう疑問に対してとことん突き止めたくなっちゃうんですよね〜

外の人から布はほつれているように見えるのか

超弦理論のモチベーション

　物理学の一つの目標として一つの理論から, 全てを説明できるようにするということが挙げられます. 例えば高校生の時に学習した電磁気学というものはわかりやすいと思います. これは18世紀後半から19世紀前半にかけて電気に関する物理と磁気に関する物理が統一されてMaxwell方程式が編み出されました. その後にも電磁気力と弱い力を統一する理論も完成されました.
　さらに強い力も含めた理論がStandard modelです. この理論にはまだ穴があってニュートリノの質量を含めていないところ, 実験をもって決めないといけないパラメータが多いところ, 暗黒物質や暗黒エネルギーについて記述されていないなどなどたくさんあります. その中でも重力について触れられていない所が特に問題かなと思います. これらを諸々含めて統一しようとした万物の理論として, 現在提唱されているものが超弦理論です.

超弦理論概略

　超弦理論では弦の振動モード(励起)の種類によって, エネルギーや質量が定まり素粒子の種類が分類されています. またそれぞれの振動モード(励起)に対応して弦のtension(張力)が定まります. これが大事なことの一つでしょう.

　次に超弦理論の計算を進めることで次元が10次元であることが言えるらしいです. ですが現在我々が住んでいるのは4次元ですよね. この$10-4$の6次元のことを余剰次元と呼び, この空間はプランク長スケールの多様体(カラビ・ヤウ多様体)としてコンパクト化していると考え, 普段生活している分には見えないとされています. これは長さとエネルギーには不確定性関係から逆数っぽい関係にあり, プランク長は$\ell_p \simeq 10^{-35} \; \text{m}$であるから, その余剰次元の観測に必要なエネルギーは$10^{19} \; \text{GeV}$となります. この超高エネルギー空間ゆえ, 低ネルギーである我々からは見ることはできないのです. 現在のLHCでは最高エネルギーが$13.6 \; \text{TeV}$らしいので, 到底及びませんね.

コンパクト化について, 例えば適切な座標が定められた一次元の直線を考えてみてください. $2\pi$ごとに同一視することを行えば円周と見分けられないですよね. 6次元空間に対して同じように同一視するという境界条件を課すことによって小さくコンパクトな空間を構成することができるのです.

　古典弦の作用の係数にtensionが入っているように, 時空間とtensionには大きな関係があります. それに伴って余剰次元とtensionは関連しているのです.

シャツはどう見えるか

　準備が整いました. それでは「シャツをハサミで切った時に我々からは布がほつれて見えるのかどうか」を考えていきます.

　そもそもシャツの切口はtensionで特徴付けられ, 弦の場と対応できます.

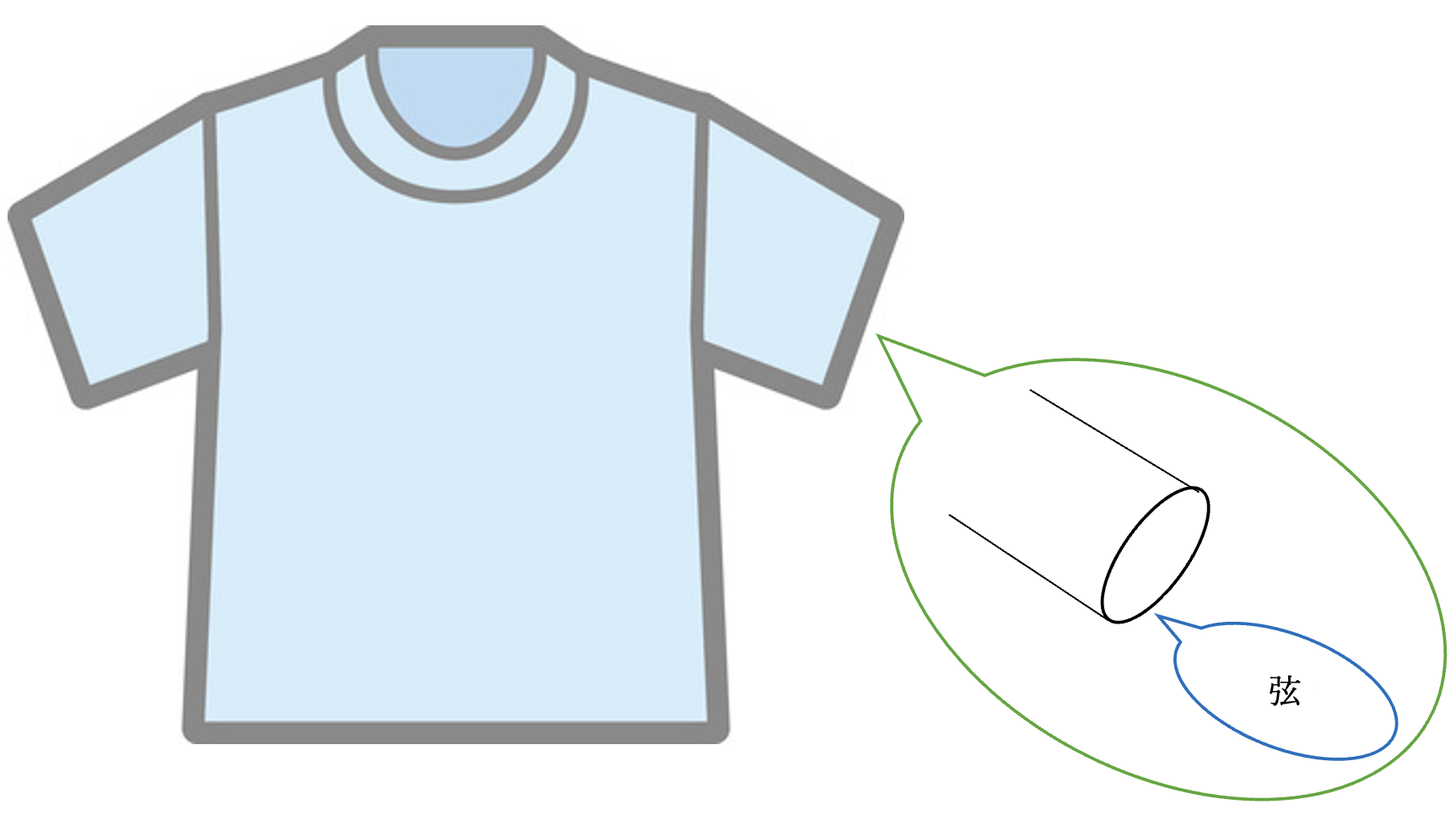シャツの袖と弦

これをハサミで切ると, 編んでいる布が途中で切られるためギザギザしているように感じます. このギザギザは振動する弦と対応することができます. このギザギザして平面から飛び出た部分は, 系全体に比べて非常に小さく, 超高エネルギーの一つの励起として扱えます. それは超高エネルギーゆえ余剰次元に押しこまれます. 図5Calabiのような感じです.

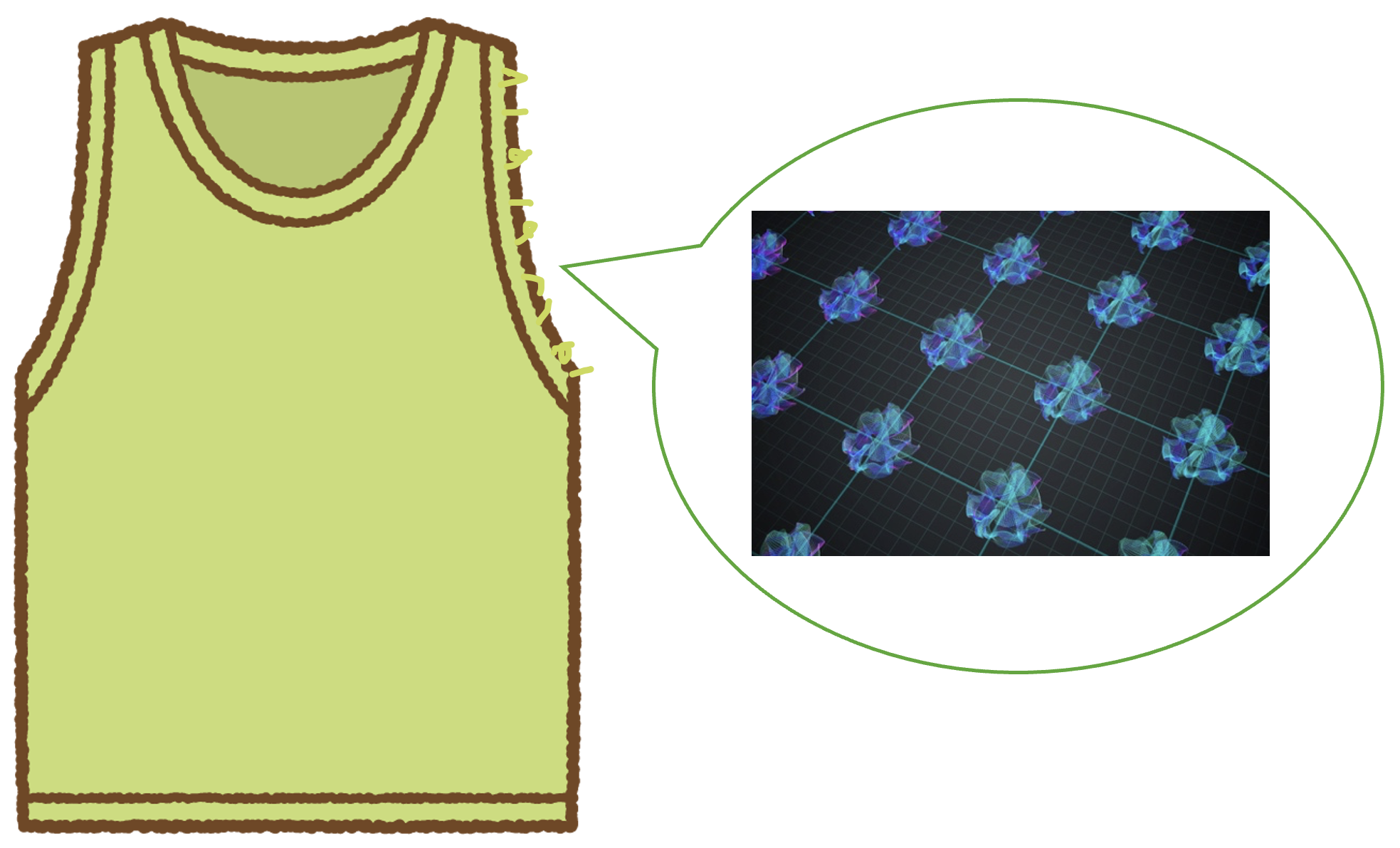ほつれた糸とカラビ・ヤウ多様体

コンパクト化された余剰次元は我々の低エネルギーでは観測することはできません. 以上より実際にギザギザしていたとしても外の観測者からは, 布がほつれているようには見えないという結論が得られました.

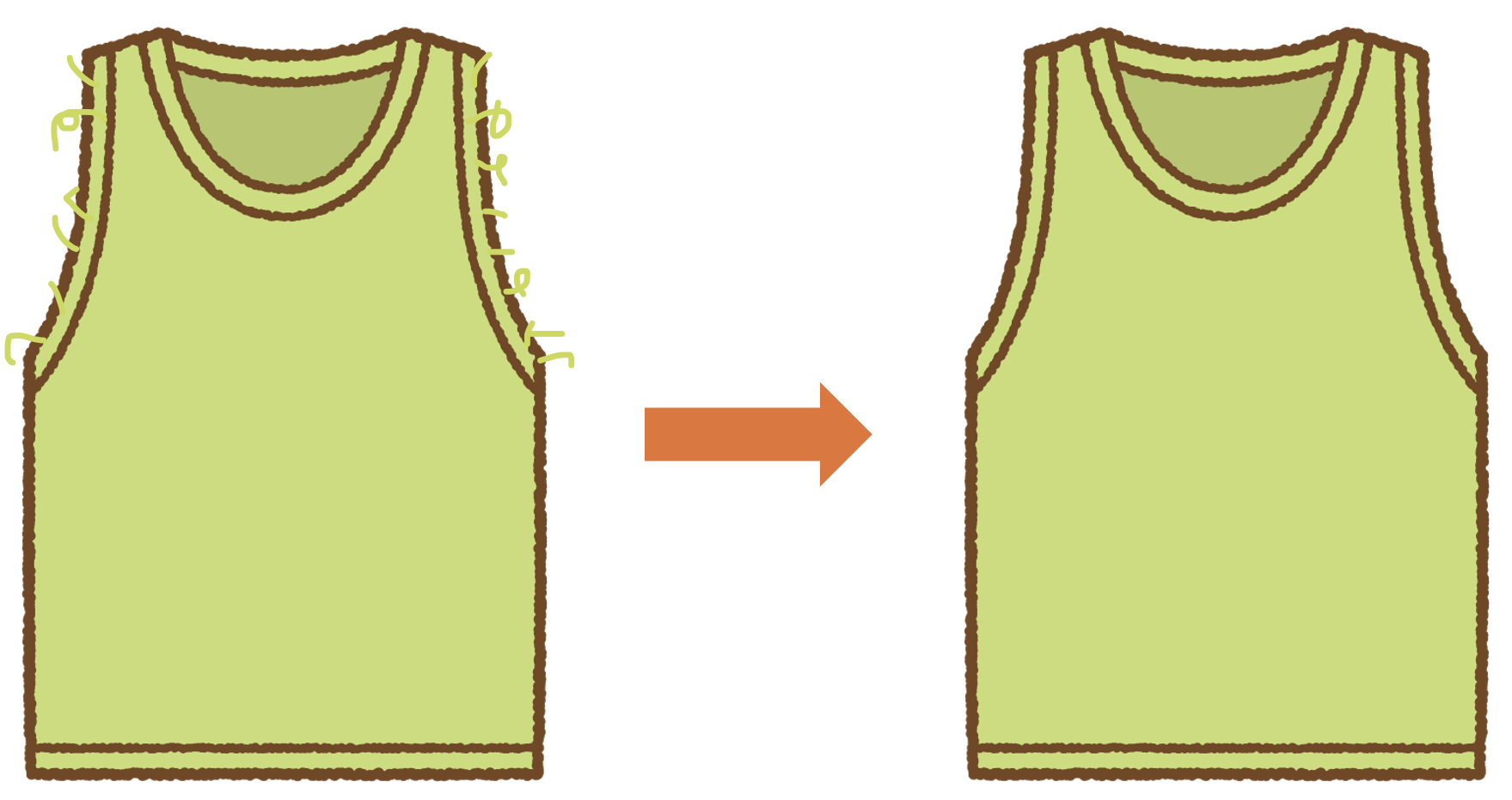観測者からみたタンクトップ

超高エネルギーかどうかは, 系全体に比べた大きさに依存しそうなので微妙な点ではありますが, 認めました. 　

終わりに

　ハサミで服を切ることで布がほつれて見えるのかどうか(自明におかしい)がわかったかもしれませんね. でも変なこと言わず, 普通に見ればほつれていてギザギザも見えますよね... ではどうすればタンクトップを作り出すことができるでしょうか？とても簡単でネットショッピングすればよかったですね.
　それでは皆さん, 強い物理学徒になるために明日からタンクトップ, 半ズボン, サングラスの格好をしてお会いしましょう.

強い物理学徒