院解11 京大数学系 H25 数学I 1 行列の交換団の可換性

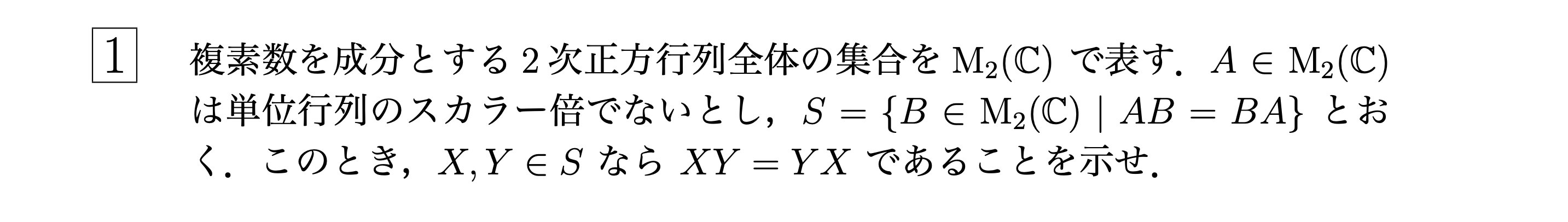
$A$の固有値の状況に応じて場合分けする.

(i)$A$が相異なる固有値$\alpha_1$,$\alpha_2$をもつとき.$\alpha_1,\alpha_2$に対応する固有ベクトルをそれぞれ$x_1,x_2$とする.
$AXx_i=XAx_i=\alpha_i Xx_i$, ($i=1,2 $)なので$Xx_i$はそれぞれ固有値$\alpha_i$に対応する$A$の固有ベクトルである.よって,ある$c_i\in \mathbb{C}$が存在して$Xx_i=c_i x_i$, ($i=1,2$).$Y$についても同様なので$Yx_i=c_i^{\prime}x_i$とおくと
$XYx_i=c_i c_i^{\prime}x_i=YXx_i$,($i=1,2$) であり,$\{x_1,x_2\}$は$\mathbb{C}^2$の底をなすから$XY=YX$.

(ii)$A$がただ一つの固有値$\alpha$をもち,$\alpha$に対応する固有空間の次元が$2$のとき,対角化により$A$は単位行列のスカラー倍なので仮定に反する.

(iii)$A$がただ一つの固有値$\alpha$をもち,対応する固有空間の次元が$1$のとき.共役によって可換性の条件は変わらないから$A$はジョルダン標準形であるとしてよい.そこで
$A= \begin{eqnarray} \left( \begin{array}{cc} \alpha & 1 \\ 0 & \alpha \end{array} \right) \end{eqnarray} $とする.$X= \begin{eqnarray} \left( \begin{array}{cc} x & y \\ z & t \end{array} \right) \end{eqnarray} $とおくと,$AX=XA$の両辺の各成分を比較して$X= \begin{eqnarray} \left( \begin{array}{cc} x & y \\ 0 & x \end{array} \right) \end{eqnarray} $をえる.$Y\in S$とすると同様に$Y= \begin{eqnarray} \left( \begin{array}{cc} x^\prime & y^\prime \\ 0 & x^\prime \end{array} \right) \end{eqnarray} $とおける.$XY=YX$であることが計算によりわかる.