【コラッツ予想の証明まとめ】一般項における証明のステップをわかりやすく！
任意の正の整数nに対して、以下で定められる操作について考える。
・nが偶数の場合、nを2で割る
・nが奇数の場合、nに3をかけて1を足す
このとき、どんなnからはじめても、有限回の操作のうちに必ず1に到達する。
この予想を証明するには何が必要か、考えてみます。
まずは、計算過程を図（ツリー図）にしてみる
1から始めて、計算を逆に考えます。
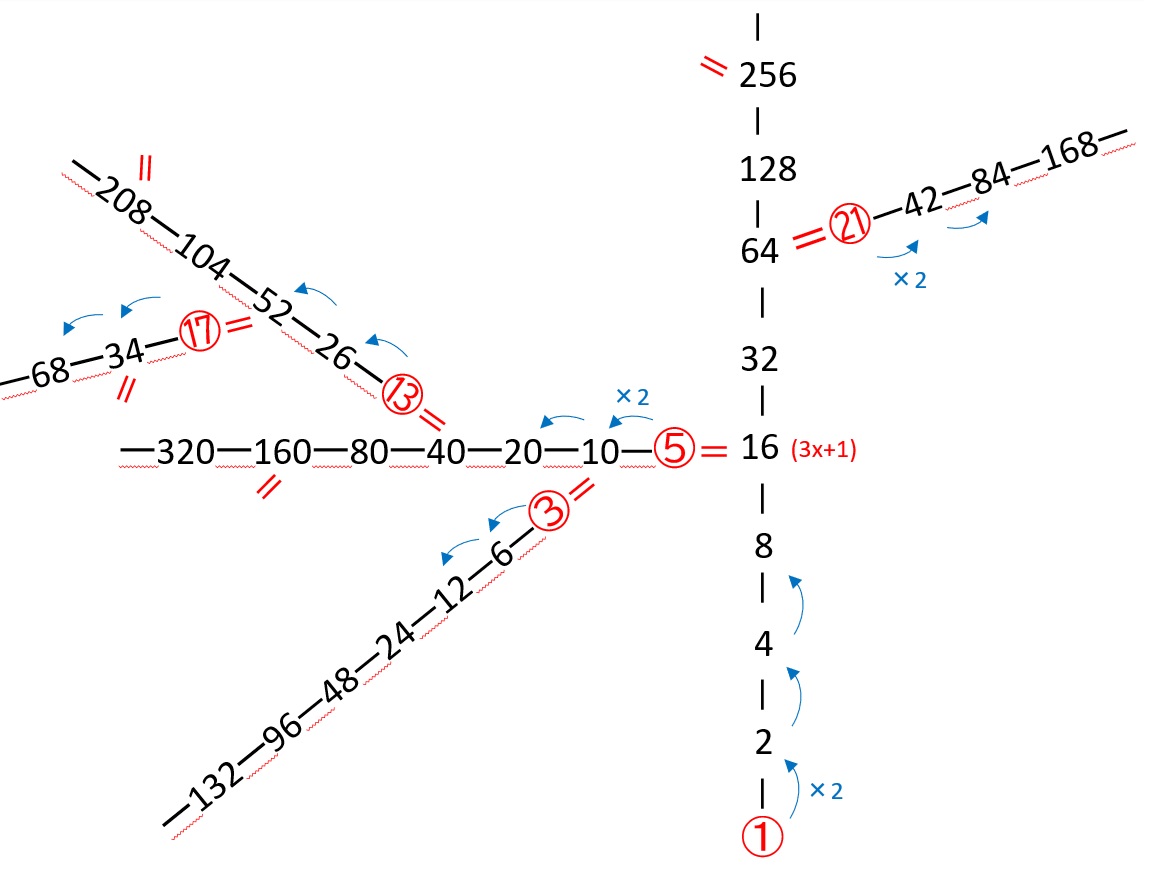コラッツ計算のツリー図
半直線の枝になっているのは偶数の数列です。
偶数は、枝ごとに奇数を2倍2倍して連なっていっていることが見てとれ、これは公比2の等比数列であるとわかります。
偶数は、3x+1タイプの偶数で奇数に分岐します。（ = 1を引いて3で割る）
一本の偶数の枝から分岐している奇数を並べると、公比4の等比数列を差とした階差数列であることがわかります。
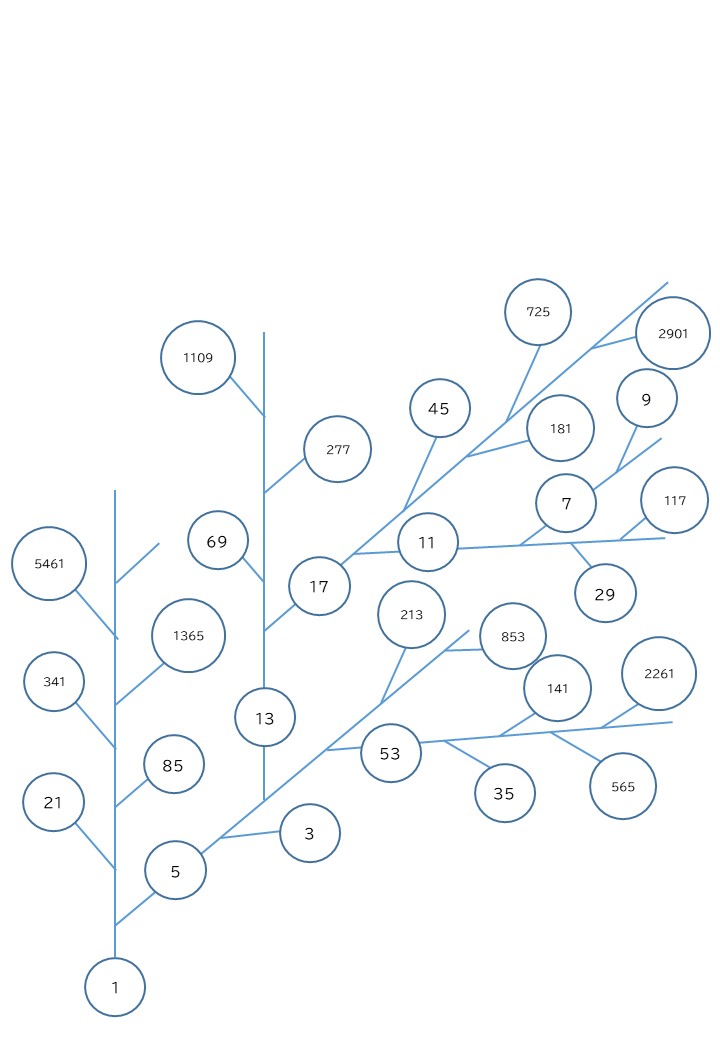奇数のみのツリー図
このことより、偶数、奇数、それぞれについて、二変数の一般項を推測できました。
一般項についての記事はこちら
証明のステップを考えてみる
流れをまとめると、
コラッツ逆計算における、偶数奇数の並びの一般項（変数が2つの二重数列）を示す
↓
変数s,tがすべての自然数をとるときに、一般項が成り立つことを数学的帰納法によって証明
↓
すべての偶数・奇数で、一般項が成り立つことを数学的帰納法によって証明
すべての奇数で、この一般項が成り立つということは、3 → 5, 13 → 5, 53 → 5, 213 → 5, 853 → 5… のように、どんな奇数も次の奇数が決まっているということです。その関係は、{3, 13, 53, 213, 853… } → 5, {9, 37, 149, 597, 2389… } → 7 のように多→1の多分木となります。すべての{}（一般項b_e,b_o）には、奇数は1つずつしかありませんので、ループすることはありません。すべての奇数において、この参照（→6t-5,6t-1）が成立しますが、ただひとつ、1 → 1 のみ、同じ数の参照となるので、すべての奇数は、一通りのパスで1に到達します。
↓
すべての自然数はコラッツの計算により、1に到達する
↓
コラッツ予想は真である
このようなステップを踏んで、証明を組み立てました。
これらの証明は
kindle数学短編小説『あの日の数式』
後半の附録ノートにまとめています。