マトロイドに対する貪欲法の最適性
はじめに
組合せ最適化問題に対するアルゴリズムの一つに貪欲法というものがあります。貪欲法は処理がシンプルで扱いやすい一方、任意の問題に対しては最適性を保証できません。そのため、最適性を保証できる条件としてマトロイドという構造が研究されています。
本記事ではマトロイドに対する貪欲法がなぜ最適性を保証できるのかを解説するのですが、細かいレベルでの解説ではなく、全体像を伝えることを目標に、次の4つのポイントを解説します：①要素数の局所最大性、②要素数の大域最大性、③要素追加の最早性、④重みの最大性。「マトロイドと貪欲法の関係性がパッとは分からなかったけど、こんな特徴を経由してこんな風に繋がっているのか」ということが伝わりますと幸いです。
本記事の内容は参考文献[1]を参考に勉強したものを筆者が再構成したものです。内容・記号・用語が異なることがありますし、間違いが含まれている可能性があります。ご注意ください。
準備
本記事で扱う記号と用語を定義します。
実行可能集合族
最適化問題のベースとなる実行可能集合族を定義します。
- $n$：台集合の要素数
- $E = \{ e_1, ..., e_n \}$：台集合
- $\F \subseteq 2^E$：実行可能集合族
- $S \subseteq E$に対して$\F | S = \{ X \in \F : X \subseteq S \}$：$S$内の実行可能集合族（実行可能集合のうち$S$に含まれているもの）
例で確認
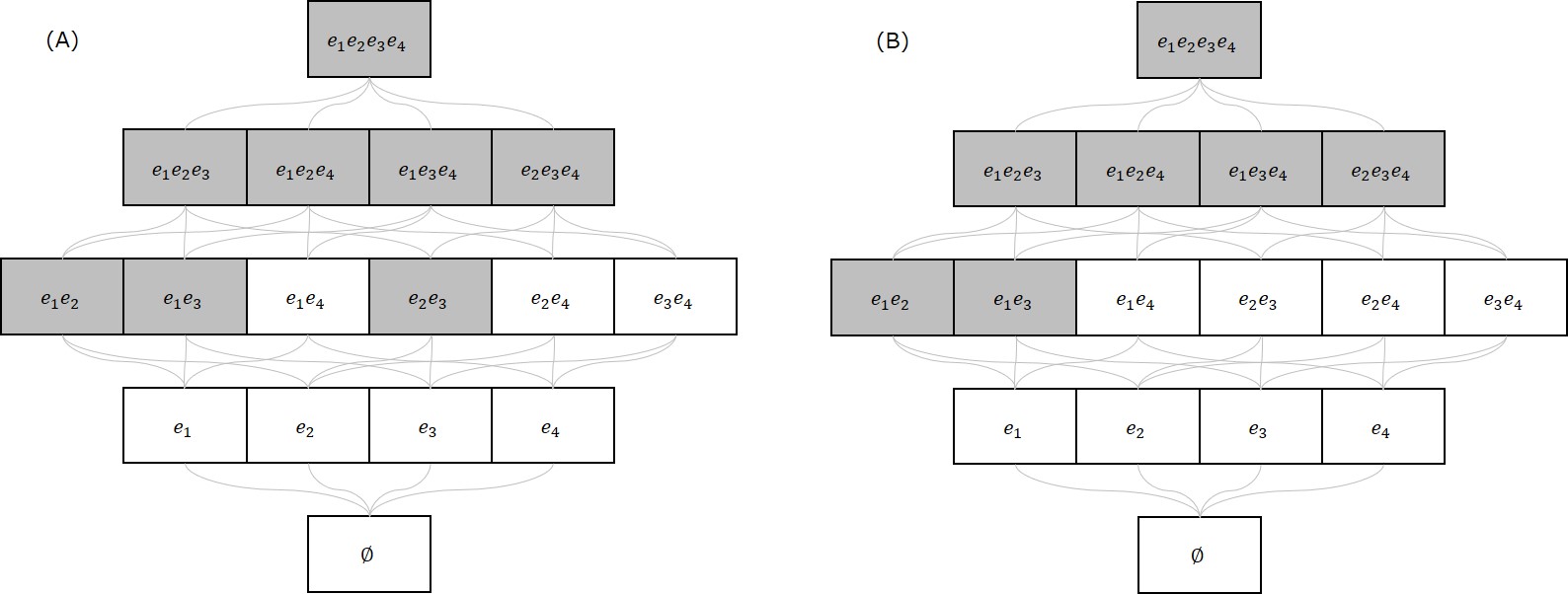
以下の図に実行可能集合族の例を示します。白色が実行可能集合、灰色が実行不能集合です。(A)(B)はそれぞれ以下の実行可能集合族$\F_{\text{A}}, \F_{\text{B}}$を図示したものです。（以降の説明でもこの例を使っていきます。）(A)と(B)はほとんど同じ集合族ですが、(B)だけに$\{ e_2, e_3 \}$があります。
$\F_{\text{A}} = \{ \emptyset, \{ e_1 \}, \{ e_2 \}, \{ e_3 \}, \{ e_4 \}, \{ e_1, e_4 \}, \{ e_2, e_4 \}, \{ e_3, e_4 \} \}$
$\F_{\text{B}} = \{ \emptyset, \{ e_1 \}, \{ e_2 \}, \{ e_3 \}, \{ e_4 \}, \{ e_1, e_4 \}, \{ e_2, e_3 \}, \{ e_2, e_4 \}, \{ e_3, e_4 \} \}$
実行可能集合族
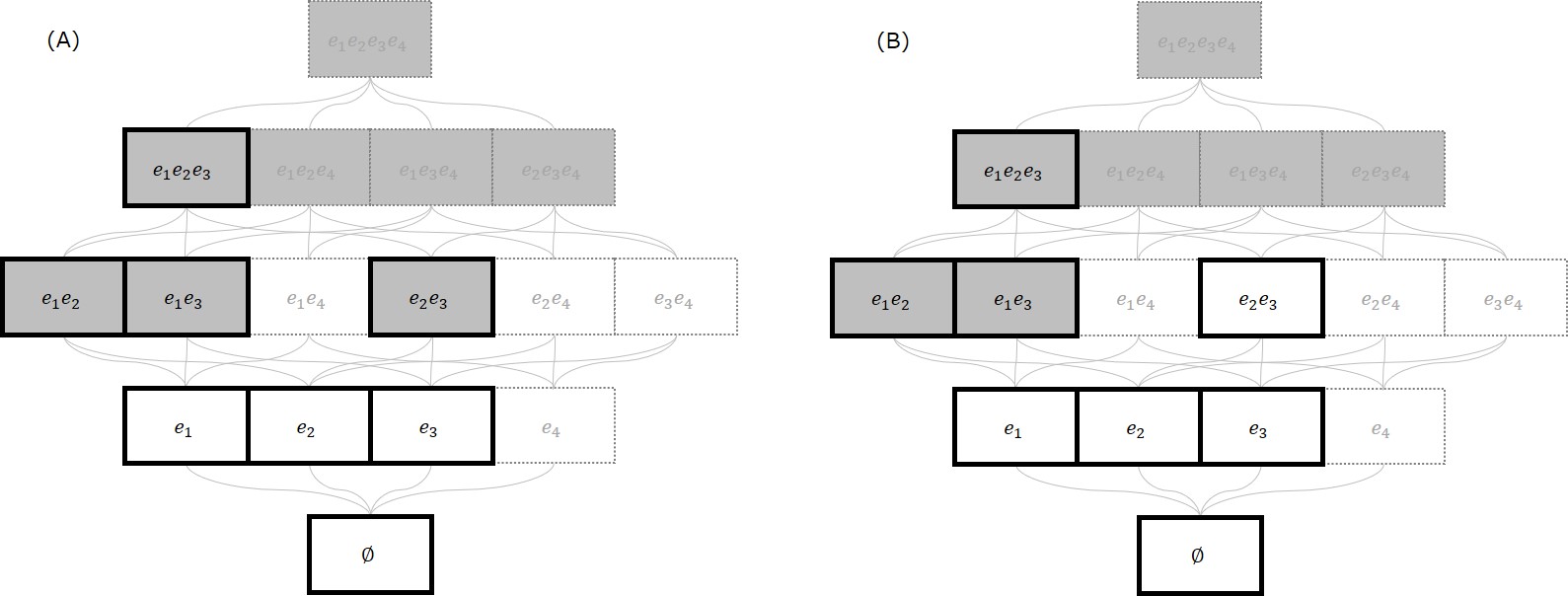
以下の図に$S = \{ e_1, e_2, e_3 \}$内の実行可能集合族の例を示します。$S$内の集合は枠線を太く、$S$外の集合は文字を薄くしています。$S$に含まれる集合だけが実行可能となり、$\F_{\text{A}} | S = \{ \emptyset, \{ e_1 \}, \{ e_2 \}, \{ e_3 \} \}$、$F_{\text{B}} | S = \{ \emptyset, \{ e_1 \}, \{ e_2 \}, \{ e_3 \}, \{ e_2, e_3 \} \}$となります。
部分集合内の実行可能集合族
マトロイド
本記事の主役であるマトロイドを定義します。
以下の条件を満たす$\F$をマトロイドと呼ぶ。
\begin{align}
& \text{(M1)} && \emptyset \in \F \\
& \text{(M2)} && \forall X \in \F, \forall Y \subseteq X : Y \in \F \\
& \text{(M3)} &&
\forall X, Y \in \F :
\left\{
|X| > |Y|
\Rightarrow
\left\{
\exists e \in X \setminus Y :
Y \cup \{ e \} \in \F
\right\}
\right\}
\end{align}
(M1)(M2)を独立集合性（仮定1）、(M3)をマトロイド性（仮定2）と呼ぶことにします。
例で確認
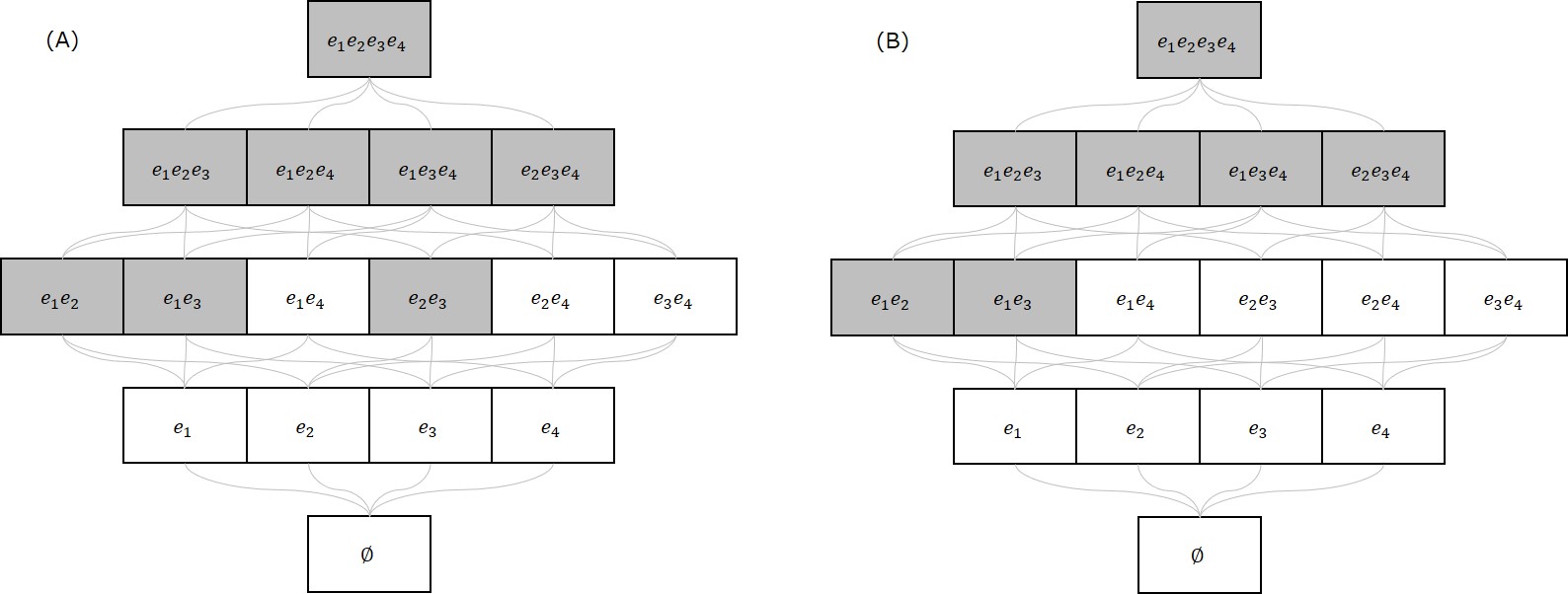
以下の図（再掲）にマトロイドと非マトロイドの例を示します。(A)は条件をすべて満たしていますのでマトロイドです（説明略）。一方で、(B)は$X = \{ e_2, e_3 \}, Y = \{ e_1 \}$とすると、$e_2, e_3 \in X \setminus Y$に対して$Y \cup \{ e_2 \} = \{ e_1, e_2 \} \not \in \F, Y \cup \{ e_3 \} = \{ e_1, e_3 \} \not \in \F$であり、(M3)を満たさなくなるためマトロイドではありません。
マトロイドと非マトロイド
重み最大化問題
本記事で扱う最適化問題を定義します。
- $w : E \rightarrow \R_+$：重み関数（非負に制限していることに注意）
所与の$\F$と$w$に対して、以下の問題を重み最大化問題と呼ぶ。
\begin{align}
\underset{X \subseteq E}{\text{maximize}} && f(X) &= \sum_{e \in X} w(e) \\
\text{subject to} && X &\in \F
\end{align}
重みを非負に制限していることは重みの非負性（仮定3）、目的関数が線形であることは目的関数の線形性（仮定4）と呼ぶことにします。
例で確認
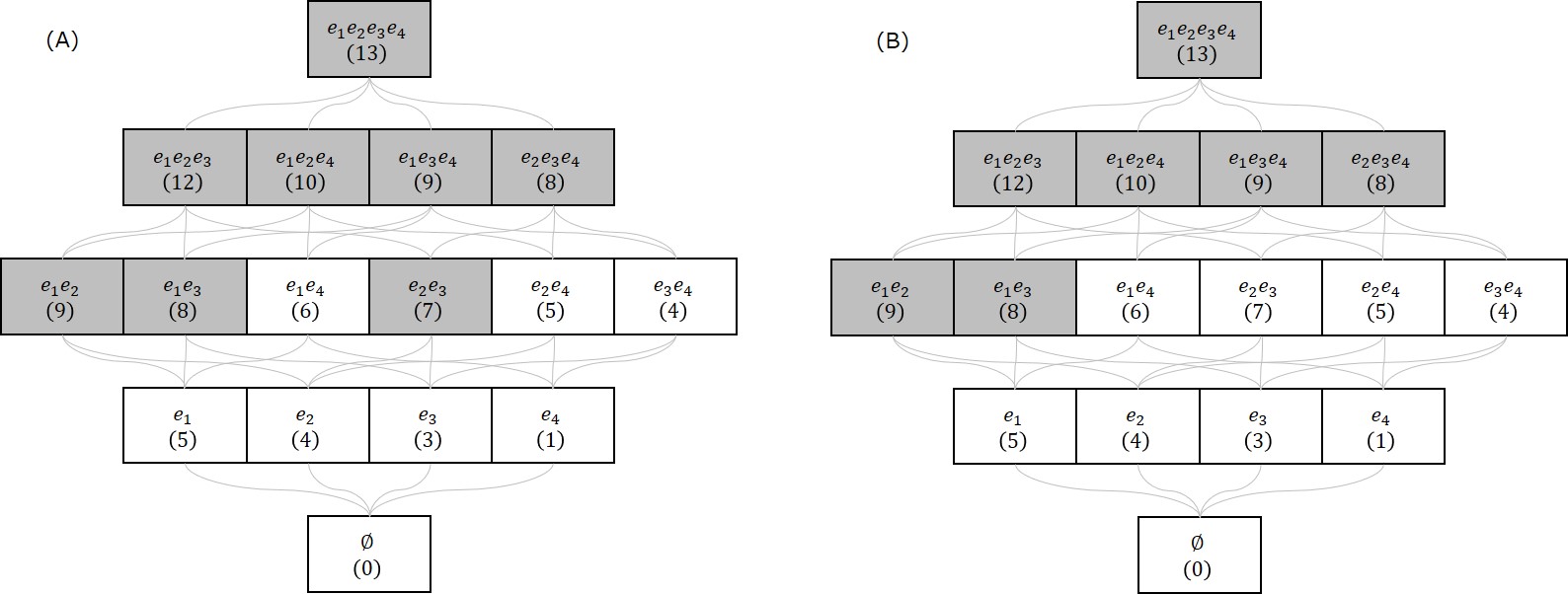
以下の図に重み最大化問題の例を示します。重み関数は$w(e_1) = 5, w(e_2) = 4, w(e_3) = 3, w(e_4) = 1$です。ボックスの括弧内に集合の重みを記載しています。(A)では$\{ e_1, e_4 \}$が重み6で最適解、(B)では$\{ e_2, e_3 \}$が重み7で最適解です。
重み最大化問題
貪欲法
最後に貪欲法を定義します。
- $E, \F, w$を入力する
- $E$の要素$e \in E$を$w(e)$が大きい順に並び変える
（$w(e_1) \geq \cdots \geq w(e_n)$と仮定） - $G \leftarrow \emptyset$
- for $i$ in $\{ 1, ..., n \}$:
- if $G \cup \{ e_i \} \in \F$ :
- $G \leftarrow G \cup \{ e_i \}$
- $G$を出力する // 本記事では貪欲集合・貪欲解と呼ぶ
2行目で要素を重みの大きい順に並びかえることをアルゴリズムの貪欲性（仮定5）、5-6行目で要素を追加した集合が実行可能であれば要素を追加することをアルゴリズムの即時追加性（仮定6）と呼ぶことにします。
例で確認
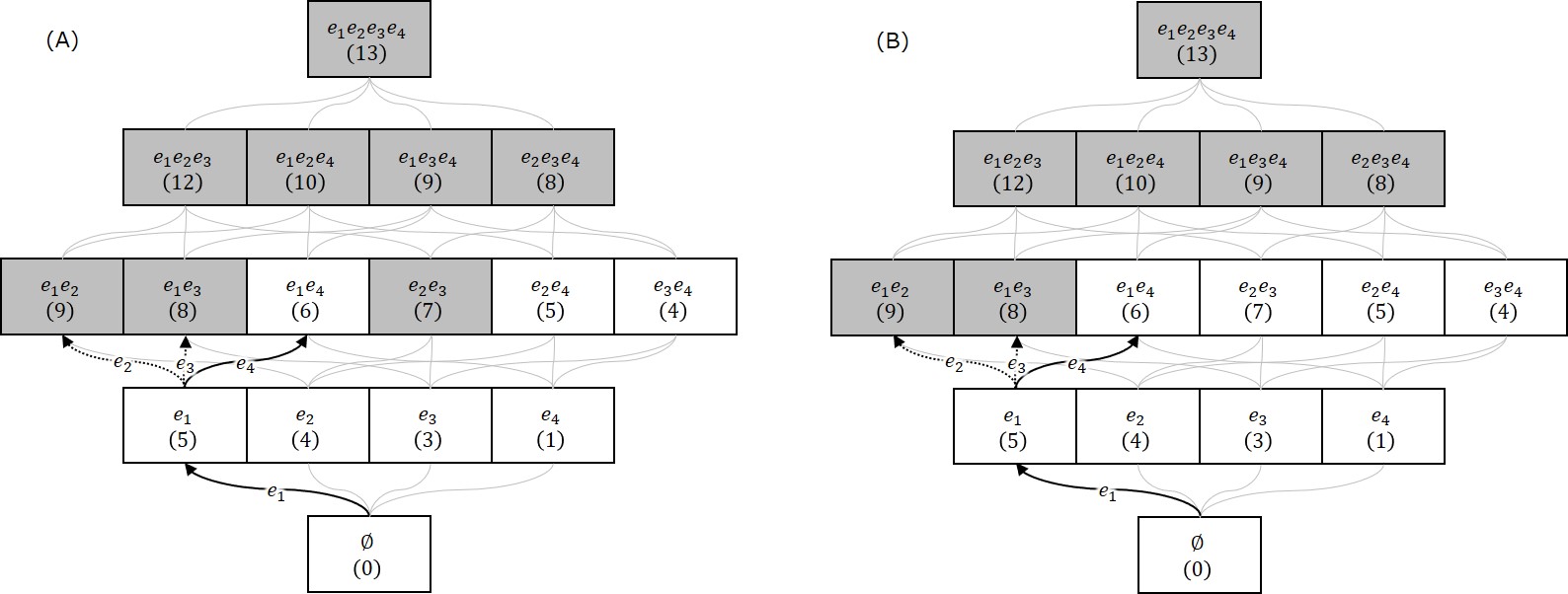
以下の図に貪欲法の挙動例を示します。(A)と(B)のどちらも同じ挙動ですので、(A)だけで説明します。(A)に対して貪欲法は以下のように挙動します。
- ステップ$i = 1$：$\emptyset \cup \{ e_1 \} \in \F$ですので、$G$に$e_1$を追加します：$G = \{ e_1 \}$。
- ステップ$i = 2$：$\{ e_1 \} \cup \{ e_2 \} \not \in \F$ですので、$G$に$e_2$は追加しません：$G = \{ e_1 \}$。
- ステップ$i = 3$：$\{ e_1\} \cup \{ e_3 \} \not \in \F$ですので、$G$に$e_3$は追加しません：$G = \{ e_1 \}$。
- ステップ$i = 4$：$\{ e_1 \} \cup \{ e_4 \} \in \F$ですので、$G$に$e_4$を追加します：$G = \{ e_1, e_4 \}$。
- $G = \{ e_1, e_4 \}$を出力
貪欲法
追加で貪欲集合$G$に関する記号を定義します。呼び方を統一するために、任意の$X \subseteq E$に対しても同様の記号を使います。以下でも$X$に対して定義します。
- $k \in \{ 1, ..., n \}$に対して$X[k]$：$X$の要素を添え字順で並べたときの先頭から$k$番目の要素
- $k \in \{ 1, ..., n \}$に対して$\step(X, k)$：$X$の$k$番目の要素を追加したステップ番号（$k > |X|$の場合については説明略）
- $i \in \{ 1, ..., n \}$に対して$E_i = \{ e_1, ..., e_i \}$：ステップ1~$i$までで追加を検討した要素の集合
- $X \cap E_i$：ステップ$i$までに追加した要素の集合（単に「ステップ$i$での集合」と呼びます。）
例で確認
$X = \{ e_1, e_4 \}$では以下となります。
- $X[1] = e_1, X[2] = e_4$
- $\step(X, 1) = 1, \step(X, 2) = 4$
- $X \cap E_1 = X \cap E_2 = X \cap E_3 = \{ e_1 \}, X \cap E_4 = \{ e_1, e_4 \}$
マトロイドに対する貪欲法の最適性
前記の図の通り、マトロイドではない(B)では最適解と貪欲解が異なっていますが、マトロイドである(A)では最適解と貪欲解が一致しています。これはたまたまではなく、実行可能集合族がマトロイドであれば任意の重み関数で成り立ちます。
実行可能集合がマトロイドであるとき、任意の重み関数に対して、貪欲解は重み最大化問題の最適解である。
4つのポイント
それでは本題に入ります。初めて定理1を見たときマトロイドと貪欲法がどこで繋がってくるのかがよく分かりませんでした。それが勉強を進めてみると、以下の4つのポイントを意識するとマトロイドと貪欲法が繋がってくることが分かってきます。まずはそれぞれのポイントを定義します。
所与の$S \subseteq E$と$X \in \F | S$に対して、$S$内で$X$の要素数が局所最大であるとは、$X$に含まれない$S$内の任意の要素を$X$に追加すると実行不能になることである。正確には次の条件を満たすことである：$\forall e \in S \setminus X : X \cup \{ e \} \not \in \F$。
例で確認
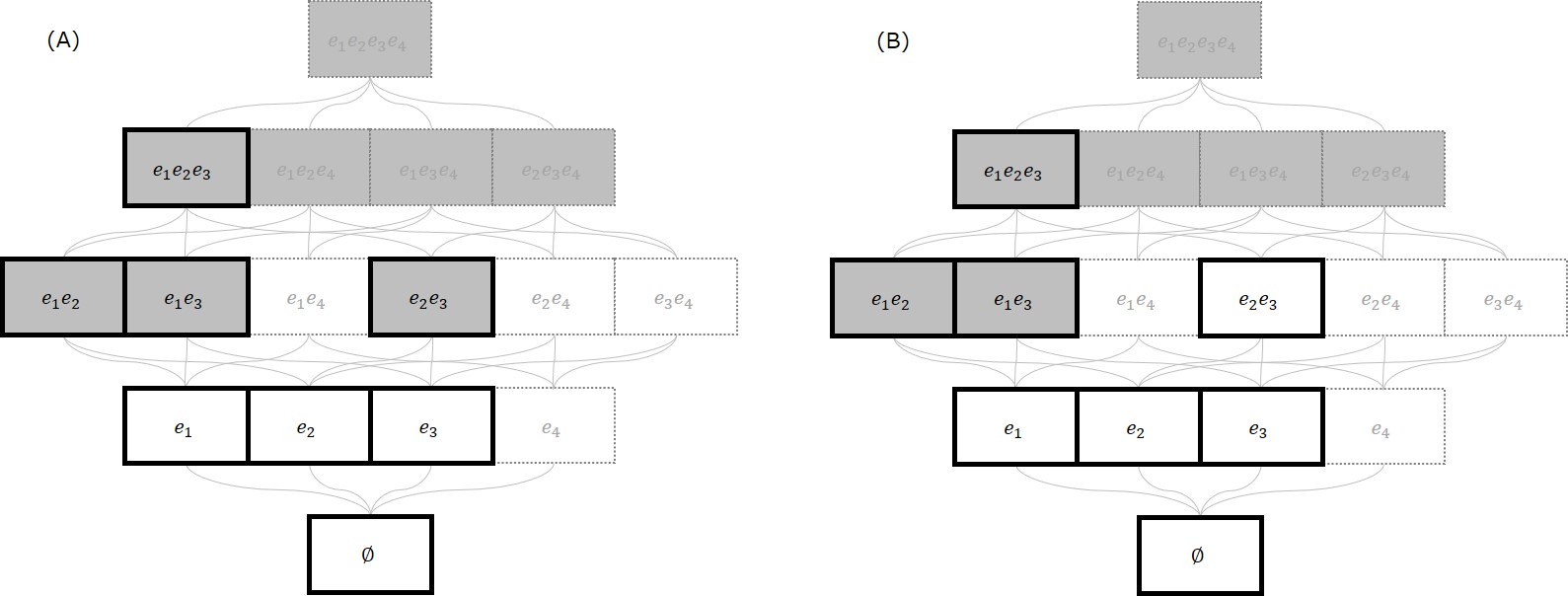
以下の図（再掲）の(B)で例を説明します。図6は$S = \{ e_1, e_2, e_3 \}$内の実行可能集合族の例です。$X = \{ e_2, e_3 \}$は$S \setminus X = \{ e_1 \}$に対して$X \cup \{e_1 \} = \{ e_1, e_2, e_3 \} \not \in \F$ですので、要素数は局所最大となります。また、$X = \{ e_1 \}$は、$S \setminus X = \{ e_2, e_3 \}$に対して、$X \cup \{ e_2 \} = \{e_1, e_2 \} \not \in \F, X \cup \{ e_3 \} = \{ e_1, e_3 \} \not \in \F$ですので、要素数は局所最大となります。
要素数の局所最大性
所与の$S \subseteq E$と$X \in \F | S$に対して、$S$内で$X$の要素数が大域最大であるとは、$X$の要素数が$S$内の任意の実行可能集合$Y \in \F | S$よりも多くなることである。正確には次の条件を満たすことである：$\forall Y \in \F | S : |X| \geq |Y|$。
例で確認
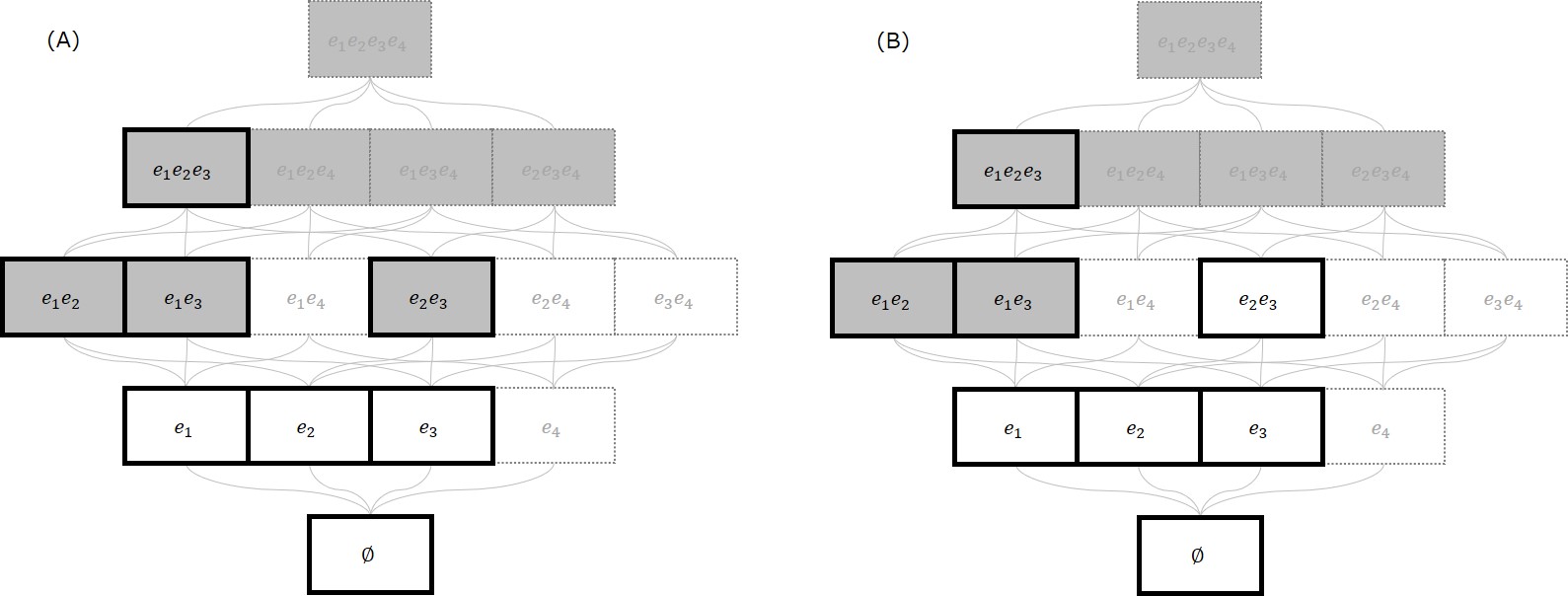
以下の図（再掲）の(B)で例を説明します。以下の図は$S = \{ e_1, e_2, e_3 \}$内の実行可能集合族の例でした。$S$内の実行可能集合の要素数を確認すると最大値は2です。$X = \{ e_2, e_3 \}$は要素数が2ですので大域最大となります。一方で、$X = \{ e_1 \}$は要素数が1ですので（局所最大ですが）大域最大ではありません。
要素数の大域最大性
所与の$X \in \F$と$k \in \{ 1, ..., n \}$に対して、$X$の$k$番目の要素の追加ステップが最早であるとは、$X$の$k$番目の要素が任意の実行可能集合$Y \in F$の$k$番目の要素よりも早く追加されていることである。正確には次の条件を満たすことである：$\forall Y \in \F : \step(X, k) \leq \step(Y, k)$。
例で確認
以下の表で例を説明します。以下の表は(A)(B)の実行可能集合族における各要素の追加タイミングを示したものです（縦方向が実行可能集合、横方向がステップ）。$X = \{ e_1, e_4 \}$の1番目の要素である$e_1$の追加ステップは1であり、他の集合の1番目の要素の追加タイミングよりも早いため、最早となります。一方で、$X$の2番目の要素である$e_4$の追加ステップは4であり、$\{ e_2, e_3 \}$の2番目の要素である$e_3$の追加ステップが3であることから、最早ではありません。
表1：要素追加の最早性
| $X$ | $i = 1$ | $i = 2$ | $i = 3$ | $i = 4$ | 備考 |
|---|---|---|---|---|---|
| $\emptyset$ | |||||
| $\{ e_1 \}$ | $X[1] = e_1$ | ||||
| $\{ e_2 \}$ | $X[1] = e_2$ | ||||
| $\{ e_3 \}$ | $X[1] = e_3$ | ||||
| $\{ e_4 \}$ | $X[1] = e_4$ | ||||
| $\{ e_1, e_4 \}$ | $X[1] = e_1$ | $X[2] = e_4$ | |||
| $\{ e_2, e_3 \}$ | $X[1] = e_2$ | $X[2] = e_3$ | (B)のみ | ||
| $\{ e_2, e_4 \}$ | $X[1] = e_2$ | $X[2] = e_4$ | |||
| $\{ e_3, e_4 \}$ | $X[1] = e_3$ | $X[2] = e_4$ |
所与の$X \in \F$に対して、$X$の重みが最大であるとは、$X$の重みが任意の実行可能集合よりも大きいことである。正確には以下の条件を満たすことである。
$\forall Y \in \F : f(X) \geq f(Y)$
例で確認
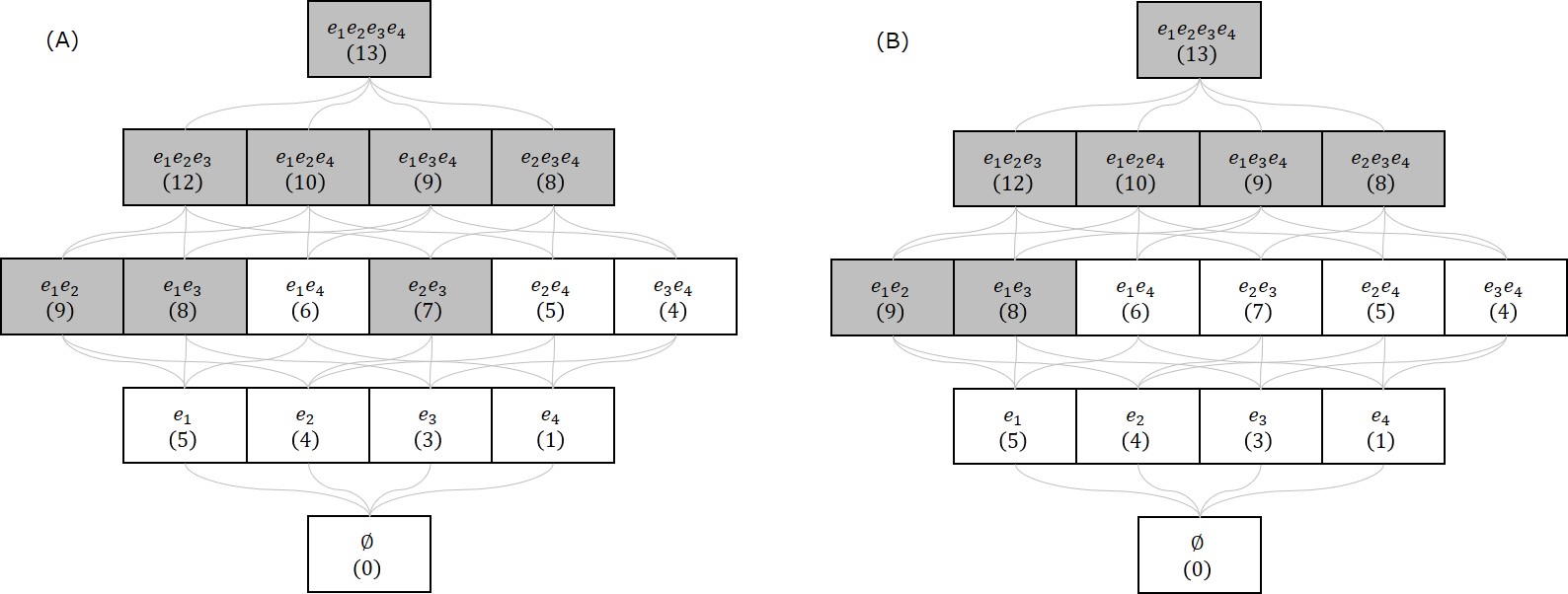
以下の図（再掲）の(B)で例を説明します。すべての実行可能集合の重みを確認すると、その最大値は7です。$X = \{ e_2, e_3 \}$は重みが7ですので最大となります。また、$X = \{ e_1, e_4 \}$は重みが6ですので最大ではありません。
重みの最大性
ポイント同士の繋がり
次に、4つのポイントがどのように繋がって、どのように最適性を示せるのかを説明します。（＋どの仮定から導かれるのか。）（補題の証明は省略。元気があれば別の記事で。）
結論として、仮定・ポイント・定理は以下の図のように繋がっています。
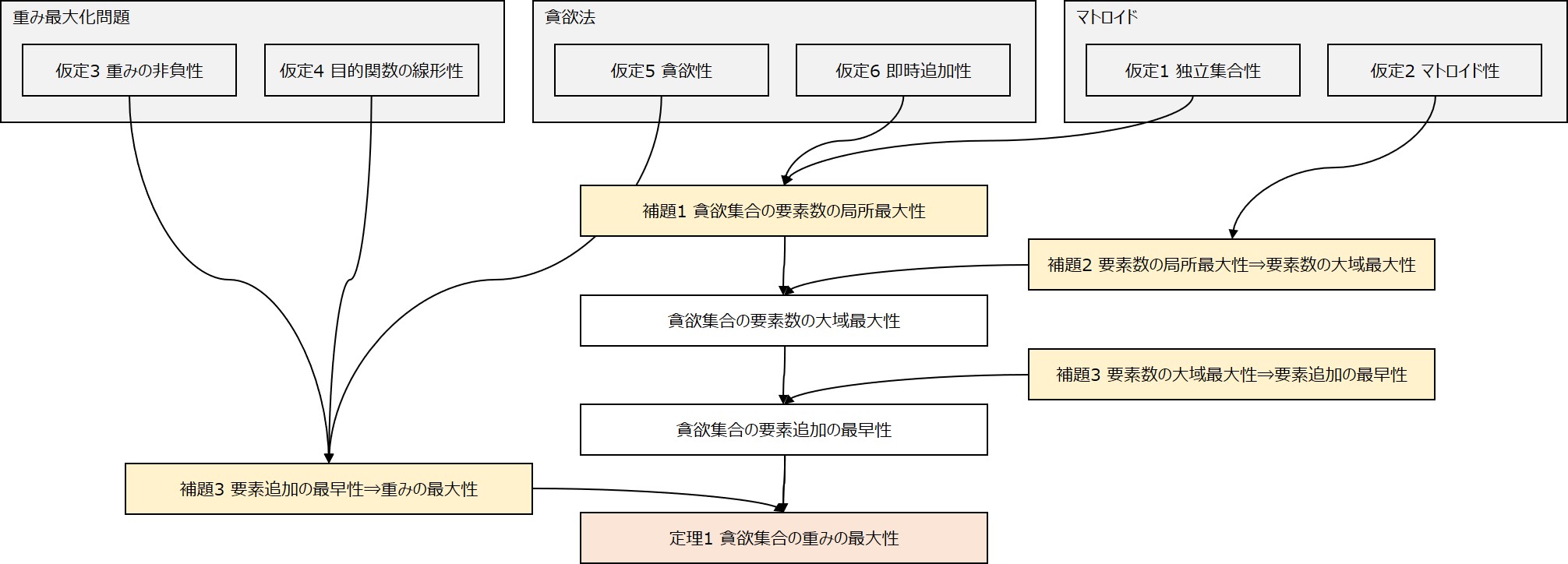ポイント同士の繋がり
まず、補題1として、任意のステップの貪欲集合は要素数が局所最大となります。これは仮定1（実行可能集合族の独立集合性）と仮定6（アルゴリズムの即時追加性）から導かれます。
例で確認
以下の図の(A)で確かめてみます。（(B)はマトロイドではありませんが、(M1)(M2)は満たしますので、要素数の局所最大性を満たしています。説明内容は(A)と同じのため省略。）各ステップを確認してみると、
- $i = 1$：追加できる要素がないため、$G \cap E_1 = \{ e_1 \}$の要素数は局所最大
- $i = 2$：$\{ e_1, e_2 \} \not \in \F$であり、$G \cap E_2 = \{ e_1 \}$の要素数は局所最大
- $i = 3$：$\{ e_1, e_2 \}, \{ e_1, e_3 \} \not \in \F$であり、$G \cap E_3 = \{ e_1 \}$の要素数は局所最大
- $i = 4$：$\{ e_1, e_2 \}, \{ e_1, e_3 \}, \{ e_1, e_4 \} \not \in \F$であり、$G \cap E_4 = \{ e_1, e_4 \}$の要素数は局所最大
であり、確かにすべてのステップで成り立っています。
貪欲集合の要素数の局所最大性
次に、補題2として、任意の部分集合内の実行可能集合は、要素数が局所最大であるとき、要素数は大域最大にもなります。これは仮定4（実行可能集合のマトロイド性）から導かれます。「任意の部分集合内で」という部分が主張を強くしているので注意です。そして、補題2を貪欲集合に適用すると、任意のステップの貪欲集合の要素数は大域最大となります。
例で確認
以下の図で確かめてみます。(A)の各ステップを確認してみると、
- $i = 1$：要素数の最大は1であり、$G \cap E_1 = \{ e_1 \}$の要素数1は大域最大
- $i = 2$：要素数の最大は1であり、$G \cap E_2 = \{ e_1 \}$の要素数1は大域最大
- $i = 3$：要素数の最大は1であり、$G \cap E_3 = \{ e_1 \}$の要素数1は大域最大
- $i = 4$：要素数の最大は2であり、$G \cap E_4 = \{ e_1, e_4 \}$の要素数2は大域最大
であり、確かにすべてのステップで成り立っています。一方で、(B)の各ステップを確認してみると、
- $i = 1$：要素数の最大は1であり、$G \cap E_1 = \{ e_1 \}$の要素数1は大域最大
- $i = 2$：要素数の最大は1であり、$G \cap E_2 = \{ e_1 \}$の要素数1は大域最大
- $i = 3$：要素数の最大は2（$\{ e_2, e_3 \}$）であり、$G \cap E_3 = \{ e_1 \}$の要素数1は大域最大ではない
- $i = 4$：要素数の最大は2であり、$G \cap E_4 = \{ e_1, e_4 \}$の要素数2は大域最大
であり、ステップ2で成り立ちません。（(B)は(M3)を満たさないから。）
要素数の局所最大性⇒要素数の大域最大性
マトロイドの定義は要素の追加に関するものですので、補題1,2で要素数の最大性に関する特徴が出てくるのは自然だと思います。ただ、目的関数は重みですから、要素数というのは最適化問題とは直接の関係はありません。ここで、要素数と重みを繋げる役割を持つのが次の補題に出てくる要素追加の最早性です。
補題3として、任意の実行可能集合は、任意のステップで要素数が大域最大であるとき、任意の$k$番目の要素の追加ステップが最早になります。そして、補題3を貪欲集合に適用すると、貪欲集合の任意の$k$番目の要素の追加ステップが最早になります。
例で確認
以下の図で確かめてみます。(A)の各$k$番目の要素を確認してみると、
- $k = 1$：最早ステップは1であり、$G[1] = e_1$の追加ステップ1は最早
- $k = 2$：最早ステップは4であり、$G[2] = e_4$の追加ステップ4は最早
であり、確かに各$k$番目の要素で成り立っています。一方で、(B)の各$k$番目の要素を確認してみると、
- $k = 1$：最早ステップは1であり、$G[1] = e_1$の追加ステップ1は最早
- $k = 2$：最早ステップは3（$\{ e_2, e_3 \}$）であり、$G[2] = e_4$の追加ステップ4は最早ではない
であり、2番目の要素で成り立ちません。（(B)は要素数の大域最大性を満たさないから。）
表2：要素数の大域最大性⇒要素追加の最早性
| $X$ | $i = 1$ | $i = 2$ | $i = 3$ | $i = 4$ | 備考 |
|---|---|---|---|---|---|
| $\emptyset$ | |||||
| $\{ e_1 \}$ | $X[1] = e_1$ | ||||
| $\{ e_2 \}$ | $X[1] = e_2$ | ||||
| $\{ e_3 \}$ | $X[1] = e_3$ | ||||
| $\{ e_4 \}$ | $X[1] = e_4$ | ||||
| $\{ e_1, e_4 \}$ | $X[1] = e_1$ | $X[2] = e_4$ | |||
| $\{ e_2, e_3 \}$ | $X[1] = e_2$ | $X[2] = e_3$ | (B)のみ | ||
| $\{ e_2, e_4 \}$ | $X[1] = e_2$ | $X[2] = e_4$ | |||
| $\{ e_3, e_4 \}$ | $X[1] = e_3$ | $X[2] = e_4$ |
補題3はマトロイドや貪欲法の特徴を使っていない点が興味深いなと思いました。要素数の大域最大性の「任意のステップで」という部分が強いことが効いているのではないかと思います。
最後に、補題4として、任意の集合は、任意の$k$番目の要素の追加ステップが最早であるとき、重みの和が最大になります。これは仮定3（重みの非負性）・仮定4（目的関数の線形性）・仮定5（アルゴリズムの貪欲性）から導かれます。これを貪欲集合に適用すると、貪欲集合の重みの和は最大になります。
例で確認
以下の図で確かめてみます。(A)では、重みの最大値6に対して、$f(\{ e_1, e_4 \}) = 5 + 1 = 6$ですので、$G$の重みは最大です。一方で、(B)では、重みの最大値7（$f(\{ e_2, e_3 \}) = 4 + 3 = 7$）に対して、$f(\{ e_1, e_4 \}) = 5 + 1 = 6$ですので、$G$の重みは最大ではありません。（要素追加の最早性が満たされていないから）
要素追加の最早性⇒重みの最大性
アルゴリズムの貪欲性から先頭の要素の方が重みが大きいですので、要素追加のタイミングというのが重みの最大性に繋がっているわけです。
おわりに
以上を簡潔にまとめると、マトロイドと貪欲法というのは、要素数の局所最大性⇒要素数の大域最大性⇒要素追加の最早性⇒重みの最大性という流れで繋がっています。マトロイドの本質として要素数の最大性に関するポイントが出てくることは当然面白いのですが、要素数と最適化問題（重み）をつなげる役割を持つ要素追加の最早性の方が、私としては惹かれるところがあります。
実は参考文献[1]では要素追加の最早性というポイントは扱っておらず、目的関数の式変形でいつの間にか要素数の最大性が重みの最大性に入れ替わっています。要素追加の最早性はこれが一体どういうことなのか（そのお気持ち）を理解しようとして出てきた概念になります。（一方で間違っている可能性も高いところになります。。）
憧れのマトロイドの理解が深まって嬉しいです。これからもマトロイドの勉強を進めてきます。
