浮動小数点演算を使用しない新しいDeepLLLアルゴリズムfracDeepLLLの提案
はじめに
前回の記事 で，浮動小数点演算を使用しない新しいLLLアルゴリズムであるfracLLLの提案を行いました．LLLの実装ができたということはDeepLLL（LLL with deep-insertion）(Schnorr and Euchner)の実装も可能であるということを示唆しています．DeepLLLはLLLの一般化で，より簡約された基底を出力することが実験的にも知られています．しかし，LLLは浮動小数点演算の誤差を考慮した$L^2$アルゴリズム(Nguyen and Stehlé, 2005)やGram-Schmidtの直交化法の代わりにHouseholder法を利用したHLLL(Morel, Stehlé and Villard, 2009)などの実装上の改良が多くあるものの，DeepLLLにはそのような改良はほとんどありません．そこで，本記事では前回提案したfracLLLをdeep型にしたfracDeepLLLを提案します．
準備
※ほとんど 前回の記事 と重複していますので，適宜読み飛ばしていただいても差し支えありません．
記号の準備
本記事で使用する記号は以下の表に従います．
| 記号 | 意味 |
|---|---|
| $\mathbb{Z}$ | 整数全体の集合 |
| $\mathbb{Q}$ | 有理数全体の集合 |
| $\mathbb{R}$ | 実数全体の集合 |
| $\mathrm{M}_n(R)$ | 環$R$上の$n\times n$行列全体の集合 |
| $\boldsymbol{O}_{n, m}$ | $n\times m$の零行列 |
| $\boldsymbol{E}_n$ | $n$次単位行列 |
| $q^{(\text{num})}$, $q^{(\text{den})}$ | $q\in\mathbb{Q}$の分子，及び分母（必ずしも既約分数とは限らない） |
| $\round{\bullet}$ | 実数の四捨五入 |
格子
一次独立な$n$本のベクトル$\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\in\mathbb{R}^n$（これを基底ベクトルと呼ぶ）の整数係数の一次結合全体の集合
$$L=\mathcal{L}(\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n):=\left\lbrace \left.\sum_{i=1}^na_i\boldsymbol{b}_i~\right|~a_1,\ldots.a_n\in\mathbb{Z}\right\rbrace$$
を(完全階数な)格子と呼び，基底ベクトルの組$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$を基底と呼ぶ．
また，基底ベクトルが全て整数ベクトルであるとき，$L$を整数格子と呼び，本記事では整数格子のみ扱う．
Gram-Schmidtの直交化法
$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$を$n$次元格子$L$の基底とする．このとき
$$\left\{\begin{aligned}\boldsymbol{b}_1^\star &:= \boldsymbol{b}_1, \\\boldsymbol{b}_i^\star &:= \boldsymbol{b}_i - \sum_{j=1}^{i-1} \mu_{i, j} \boldsymbol{b}_j^\star,~\mu_{i, j}:=\frac{\langle \boldsymbol{b}_i, \boldsymbol{b}_j^\star\rangle}{\| \boldsymbol{b}_j^\star \|^2}~(1 \leq j < i \leq n).\end{aligned}\right.$$
で定義される$\boldsymbol{b}_1^\star,\ldots,\boldsymbol{b}_n^\star$をGram-Schmidtの直交化ベクトル，$\boldsymbol{U}\coloneqq (\mu_{i, j})_{i, j}$をGram-Schmidtの直交化係数行列と呼ぶ．
B1やB2の線形代数学で習うようなGram-Schmidtの直交化法そのものです．
DeepLLL
DeepLLL簡約はLLL簡約の自然な一般化であり，以下の様に定義されます．
$\lbrace\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\rbrace$を$n$次元格子$L$の基底とします．このとき，$\lbrace\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\rbrace$が簡約パラメタ$\frac{1}{4}<\delta<1$に対してDeepLLL簡約されているとは
$$
\begin{array}{ll}
&(\textbf{サイズ簡約条件})&1\le{}^\forall j<{}^\forall i\le n,&\lvert\mu_{i, j}\rvert\le \frac{1}{2}\\
&(\textbf{deep-exchange条件})&1\le{}^\forall i<{}^\forall k\le n,&\delta\lVert \boldsymbol{b}_{i}^\star\rVert\le \lVert \pi_{i}(\boldsymbol{b}_k)\rVert^2
\end{array}
$$
を満たすときを言います．但し，写像
$$
\begin{array}{lclc}
&\pi_\ell : &\mathbb{R}^n &\longrightarrow &\langle \boldsymbol{b}_1, \dots, \boldsymbol{b}_{\ell-1} \rangle_\mathbb{R}^\perp&=\langle \boldsymbol{b}_\ell^\star, \dots, \boldsymbol{b}_n^\star \rangle_\mathbb{R}\\
&&\boldsymbol{x} &\longmapsto &\displaystyle\sum_{i = \ell}^n \frac{\langle \boldsymbol{x}, \boldsymbol{b}_i^\star \rangle}{ \| \boldsymbol{b}_i^\star \|^2 } \boldsymbol{b}_i^\star
\end{array}
$$
は$\mathbb{R}$ベクトル空間$\langle \boldsymbol{b}_1, \dots, \boldsymbol{b}_{\ell-1} \rangle_\mathbb{R}$の直交補空間への直交射影とします．
$n$次元格子$L$の基底$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$に対して，deep-insertion$\sigma_{i, k}$とは
$$
\sigma_{i, k}: \{\boldsymbol{b}_1,\ldots, \boldsymbol{b}_n\}\longmapsto \lbrace\ldots,\boldsymbol{b}_{i-1},\boldsymbol{b}_k,\boldsymbol{b}_i,\ldots,\boldsymbol{b}_{k-1},\boldsymbol{b}_{k+1},\ldots\rbrace
$$
で定義される写像である．
fracDeepLLLの理論的な部分
まず，前回も証明したように以下の補題たちが成立します．
$n$次元格子の基底$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$のGram-Schmidtの直交化ベクトルは，
$$
\boldsymbol{b}_i^\star=\sum_{j=1}^i(-1)^{j+i}\frac{d_{i, j}}{d_{i, i}}\boldsymbol{b}_j
$$
と表すことができる．ただし，$G_{i, j}\coloneqq \langle\boldsymbol{b}_i, \boldsymbol{b}_j\rangle$（これを並べた行列を基底のGram行列と呼ぶ）に対して
$$
d_{i, j}=\det\mqty[G_{1, 1}\ & \cdots & G_{1, i-1}\\
\vdots & \ddots & \vdots\\
G_{j-1, 1} & \cdots & G_{j-1, i-1}\\
G_{j+1, 1} & \cdots & G_{j+1, i-1}\\
\vdots & \ddots & \vdots\\
G_{i, 1} & \cdots & G_{i, i-1}]
$$
と定義される整数である．
$n$次元格子の基底$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$のGram-Schmidtの直交化ベクトルの二乗ノルムを$B_i\coloneqq \norm{\boldsymbol{b}_i^\star}^2~(i=1,\ldots, n)$，Gram-Schmidtの直交化係数行列を$\boldsymbol{U}\coloneqq(\mu_{i, j})$とすると，次が成立する．
$$
B_i=\frac{\sum_{j=1}^i\sum_{k=1}^i(-1)^{j+k}d_{i, j}d_{i, k}\langle\boldsymbol{b}_j, \boldsymbol{b}_k\rangle}{d_{i, i}^2},
$$
$$
\mu_{i, j}=\left\{
\begin{array}{ll}
&\!\!\!\!\!\displaystyle\frac{d_{j, j}\sum_{k=1}^j(-1)^{j+k}d_{j, k}G_{i, k}}{\sum_{k=1}^i\sum_{\ell=1}^j(-1)^{k+\ell}d_{j, k}d_{j, \ell}G_{k, \ell}}&\text{if}~~1\le j< i\le n\\
&\!\!\!\!\!1&\text{if}~~i=j\\
&\!\!\!\!\!0&\text{else}
\end{array}
\right.$$
これらを用いると，以下の命題が従います．
$\lbrace\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\rbrace$を$n$次元格子$L$の基底とする．このとき，簡約パラメタ$\frac{a}{b}$に対してdeep-exchange条件は次の様に書き換えられる．
$$
\left\{bG_{k, k}\den{B_i}-a\num{B_i}\right\}\prod_{j=1}^{i-1}\left(\den{\mu_{k, j}}\right)^2\den{B_j}\ge b\den{B_i}\sum_{j=1}^{i-1}\left[\num{\mu_{k, j}}\num{B_j}\prod_{\ell=1,\ell\ne j}^{i-1}\left(\den{\mu_{k, \ell}}\right)^2\den{B_\ell}\right]
$$
命題2に注意して分母を払えば良い．$\square$
また，基底にdeep-insertionを施した後のGram-Schmidtの直交化情報については以下の定理が成立します．
$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$を$n$次元格子$L$の基底とし，さらに別の$L$の基底を
$$
\{\boldsymbol{c}_1,\ldots,\boldsymbol{c}_n\}\coloneqq \sigma_{i, k}(\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\})
$$
とする．このとき，基底$\{\boldsymbol{c}_1,\ldots,\boldsymbol{c}_n\}$のGram-Schmidtの直交化情報$(C_j)_{1\le j\le n},~(\nu_{\ell, j})_{1\le \ell, j\le n}$は，$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$のGram-Schmidtの直交化情報$(B_j)_j, (\mu_{\ell, j})$及び$D_\ell\coloneqq \norm{\pi_\ell(\boldsymbol{b}_k)}^2$を用いて次のように表すことができる．
$$
C_j=\left\{
\!\!\!\!\!\!\begin{array}{ll}
& D_i & \text{if}~j=i\\
& \displaystyle\frac{D_jB_{j-1}}{D_{j-1}} & \text{if}~i+1\le j\le k\\
& B_j & \text{else}
\end{array}
\right.
$$
$$
\nu_{\ell, j}=\left\{
\!\!\!\!\!\!\begin{array}{lll}
&\displaystyle\mu_{\ell-1, j-1}-\frac{\mu_{k, j-1}}{D_j}\sum_{h=j}^{\ell-1}\mu_{k, h}\mu_{\ell-1, h}B_h & \text{if}~i+1\le j\le k,~j+1\le \ell\le k\\
&\displaystyle \mu_{\ell, j-1}-\frac{\mu_{k, j-1}}{D_j}\sum_{h=j}^k \mu_{k, h}\mu_{\ell, h}B_h & \text{if}~i+1\le j\le k,~k+1\le \ell \le n\\
&\displaystyle \frac{1}{D_i}\sum_{h=i}^{\ell-1}\mu_{k, h}\mu_{\ell-1, h}B_h & \text{if}~j=i,~i+1\le \ell \le k\\
& \displaystyle \frac{1}{D_i}\sum_{h=i}^{k}\mu_{k, h}\mu_{\ell, h}B_h & \text{if}~j=i,~k+1\le \ell\le n\\
& \mu_{k, j} & \text{if}~\ell=i,~1\le j\le i-1\\
& \mu_{\ell-1, j} & \text{if}~i+1\le \ell\le k,~1\le j\le i-1\\
& \mu_{\ell, j} & \text{else}
\end{array}
\right.
$$
ここから，次の系が成立します．
$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$を$n$次元格子$L$の基底とし，さらに別の$L$の基底を
$$
\{\boldsymbol{c}_1,\ldots,\boldsymbol{c}_n\}\coloneqq \sigma_{i, k}(\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\})
$$
とする．このとき，基底$\{\boldsymbol{c}_1,\ldots,\boldsymbol{c}_n\}$のGram-Schmidtの直交化情報$(C_j)_{1\le j\le n},~(\nu_{\ell, j})_{1\le \ell, j\le n}$は，$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$のGram-Schmidtの直交化情報$(B_j)_j, (\mu_{\ell, j})$及び
$$
D_\ell\coloneqq \frac{G_k\prod_{j-1}^{\ell-1}\left(\den{\mu_{k, j}}\right)^2\den{B_j}-\sum_{j=1}^{\ell-1}\left[\num{\mu_{k, j}}\num{B_j}\prod_{h=1, h\ne j}^{\ell-1}\left(\den{\mu_{k, h}}\right)^2\den{B_h}\right]}{\prod_{j=1}^{\ell-1}\left(\den{\mu_{k, j}}\right)^2\den{B_j}}
$$
を用いて次のように表すことができる．
$$
C_j=\left\{
\begin{array}{ll}
D_i & \text{if}~j=i\\
\displaystyle \frac{\den{D_{j-1}}\num{D_j}\num{B_{j-1}}}{\num{D_{j-1}}\den{D_j}\den{B_{j-1}}} & \text{if}~i+1\le j\le k\\
B_j & \text{else}
\end{array}
\right.
$$
$$
\nu_{\ell, j}=\left\{
\begin{array}{ll}
\displaystyle \frac{\displaystyle\num{\mu_{\ell-1, j-1}}\den{\mu_{k, j-1}}\den{D_j}\prod_{g=j}^{\ell-1}\den{\mu_{k, g}}\den{\mu_{\ell-1, g}}\den{B_g}-\den{\mu_{\ell-1, j-1}}\num{\mu_{k, j-1}}\den{D_j}\sum_{h=j}^{\ell-1}\left[\num{\mu_{k, h}}\num{\mu_{\ell-1, h}}\num{B_h}\prod_{g=j, g\ne h}^{\ell-1}\den{\mu_{k, g}}\den{\mu_{\ell-1, g}}\den{B_g}\right]}{\displaystyle\den{\mu_{\ell-1, j-1}}\den{\mu_{k, j-1}}\den{D_j}\prod_{g=j}^{\ell-1}\den{\mu_{k, g}}\den{\mu_{\ell-1, g}}\den{B_g}} & \text{if}~i+1\le j\le k,~j+1\le \ell\le k\\
\displaystyle \frac{\displaystyle\num{\mu_{\ell, j-1}}\den{\mu_{k, j-1}}\den{D_j}\prod_{g=j}^{k}\den{\mu_{k, g}}\den{\mu_{\ell, g}}\den{B_g}-\den{\mu_{\ell, j-1}}\num{\mu_{k, j-1}}\den{D_j}\sum_{h=j}^{k}\left[\num{\mu_{k, h}}\num{\mu_{\ell, h}}\num{B_h}\prod_{g=j, g\ne h}^{k}\den{\mu_{k, g}}\den{\mu_{\ell, g}}\den{B_g}\right]}{\displaystyle\den{\mu_{\ell, j-1}}\den{\mu_{k, j-1}}\den{D_j}\prod_{g=j}^{k}\den{\mu_{k, g}}\den{\mu_{\ell, g}}\den{B_g}} & \text{if}~i+1\le j\le k,~k+1\le \ell\le n\\
\displaystyle\frac{\displaystyle \den{D_i}\sum_{h=i}^{\ell-1}\num{\mu_{k, h}}\num{\mu_{\ell-1, h}}\num{B_h}\prod_{g=i, g\ne h}^{\ell-1}\den{\mu_{k, g}}\den{\mu_{\ell-1, g}}\den{B_g}}{\displaystyle\num{D_i}\prod_{h=i}^{\ell-1}\den{\mu_{k, h}}\den{\mu_{\ell-1, h}}\den{B_h}} & \text{if}~j=i,~i+1\le \ell\le k\\
\displaystyle\frac{\displaystyle \den{D_i}\sum_{h=i}^{k}\num{\mu_{k, h}}\num{\mu_{\ell, h}}\num{B_h}\prod_{g=i, g\ne h}^{k}\den{\mu_{k, g}}\den{\mu_{\ell, g}}\den{B_g}}{\displaystyle\num{D_i}\prod_{h=i}^{k}\den{\mu_{k, h}}\den{\mu_{\ell, h}}\den{B_h}} & \text{if}~j=i,~k+1\le \ell\le n\\
\mu_{k, j} & \text{if}~\ell=i,~1\le j\le i-1\\
\mu_{\ell-1, j} & \text{if}~i+1\le \ell\le k,~1\le j\le i-1\\
\mu_{\ell, j} & \text{else}
\end{array}
\right.
$$
通分すれば良い．
fracDeepLLLの実装
定理4 系1を利用した，効率的なGram-Schmidtの直交化情報の更新アルゴリズムについて，前回の記事のAlgorithm 4を繰り返し利用するものより効率的な方法を思いついていないので，定理4 系1を利用したアルゴリズムは今回は実装していません．
$$ \begin{array}{ll} &\!\!\!\!\!\!\!\!\!\!\!\!\textbf{Algorithm~1}~\text{update\_gso\_deep\_insertion(i, k): deep-insertion}\sigma_{i, k}\text{を施した後のGram-Schmidtの直交化情報の更新}\\ & \!\!\!\!\!\!\!\!\!\!\!\!\textbf{Input}:~\text{Gram-Schmditの直交化情報}\left(\frac{\mu_{i, j}^{(\text{num})}}{\mu_{i, j}^{(\text{den})}}\right), \left(\frac{B_{i}^{(\text{num})}}{B_{i}^{(\text{den})}}\right)\\ & \!\!\!\!\!\!\!\!\!\!\!\!\textbf{Output}:~\text{更新されたGram-Schmidt情報}\left(\frac{\nu_{i, j}^{(\text{num})}}{\nu_{i, j}^{(\text{den})}}\right), \left(\frac{C_{i}^{(\text{num})}}{C_{i}^{(\text{den})}}\right)\\ 1 & C^{(\text{num})}\gets B^{(\text{num})};~C^{(\text{den})}\gets B^{(\text{den})}\\ 2 & \nu^{(\text{num})}\gets \mu^{(\text{num})};~\nu^{(\text{den})}\gets \mu^{(\text{den})}\\ 3 & \textbf{for}~\ell=k~\text{downto}~i+1~\textbf{do}\\ 4 & \quad C^{(\text{num})}_{\ell-1}\gets B_\ell^{(\text{num})}B_{\ell-1}^{(\text{den})}\left(\mu_{\ell, \ell-1}^{(\text{den})}\right)^2+\left(\mu_{\ell, \ell-1}^{(\text{num})}\right)^2 B_\ell^{(\text{den})}B_{\ell-1}^{(\text{num})}\\ 5 & \quad C^{(\text{den})}_{\ell-1}\gets B_\ell^{(\text{den})}B_{\ell-1}^{(\text{den})}\left(\mu_{\ell, \ell-1}^{(\text{den})}\right)^2\\ 6 & \quad C^{(\text{num})}_{\ell}\gets B_{\ell-1}^{(\text{num})}B_\ell^{(\text{num})}C_{\ell-1}^{(\text{den})}\\ 7 & \quad C^{(\text{den})}_{\ell}\gets B_{\ell-1}^{(\text{den})}B_\ell^{(\text{den})}C_{\ell-1}^{(\text{num})}\\ 8 & \quad \nu_{\ell, \ell-1}^{(\text{num})}\gets \mu_{\ell, \ell-1}^{\text{(num)}}B_{\ell-1}^{\text{(num)}}C_{\ell-1}^{\text{(den)}}\\ 9 & \quad \nu_{\ell, \ell-1}^{(\text{den})}\gets\mu_{\ell, \ell-1}^{\text{(den)}}B_{\ell-1}^{\text{(den)}}C_{\ell-1}^{\text{(num)}}\\ 10 & \quad \textbf{for}~j=1~\text{to}~\ell-2~\textbf{do}\\ 11 & \quad \quad \nu_{\ell-1, j}^{(\text{num})}\gets \mu_{\ell, j}^{(\text{num})};~\nu_{\ell-1, j}^{(\text{den})}\gets \mu_{\ell, j}^{(\text{den})}\\ 12 & \quad \quad \nu_{\ell, j}^{(\text{num})}\gets \mu_{\ell-1, j}^{(\text{num})};~\nu_{\ell, j}^{(\text{den})}\gets \mu_{\ell-1, j}^{(\text{den})}\\ 13 & \quad \textbf{for}~i=\ell+1~\text{to}~n~\textbf{do}\\ 14 & \quad\quad \mu_{i, \ell}^{(\text{num})}\gets \mu_{i, \ell-1}^{\text{(num)}}\mu_{\ell, \ell-1}^{\text{(den)}}\mu_{i, \ell}^{\text{(den)}}-\mu_{\ell, \ell-1}^{\text{(num)}}\mu_{i, \ell}^{\text{(num)}}\mu_{i, \ell-1}^{\text{(den)}}\\ 15 & \quad \quad \mu_{i, \ell}^{(\text{den})}\gets \mu_{i, \ell-1}^{\text{(den)}}\mu_{\ell, \ell-1}^{\text{(den)}}\mu_{i, \ell}^{\text{(den)}}\\ 16 & \quad \quad \mu_{i, \ell-1}^{(\text{num})}\gets \mu_{i, \ell}^{\text{(num)}}\nu_{\ell, \ell-1}^{\text{(den)}}\nu_{i, \ell}^{\text{(den)}}+\mu_{i, \ell}^{\text{(den)}}\nu_{\ell, \ell-1}^{\text{(num)}}\nu_{i, \ell}^{\text{(num)}}\\ 17 & \quad\quad \mu_{i, \ell-1}^{(\text{den})}\gets \mu_{i, \ell}^{\text{(den)}}\nu_{\ell, \ell-1}^{\text{(den)}}\nu_{i, \ell}^{\text{(den)}}\\ 18 & \quad B^{(\text{num})}\gets C^{(\text{num})};~B^{(\text{den})}\gets C^{(\text{den})}\\ 19 & \quad \mu^{(\text{num})}\gets \nu^{(\text{num})};~\mu^{(\text{den})}\gets \nu^{(\text{den})}\\ \end{array} $$
$$ \begin{array}{ll} &\!\!\!\!\!\!\!\!\!\!\!\!\textbf{Algorithm~2}~\text{frac\_deep\_lll(a, b): 有理数によるDeepLLL}\\ & \!\!\!\!\!\!\!\!\!\!\!\!\textbf{Input}:~\text{格子基底}\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}, \text{簡約パラメタ}\frac{a}{b}\\ & \!\!\!\!\!\!\!\!\!\!\!\!\textbf{Output}:~\text{簡約された基底}\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}\\ 1 & \num{B}, \den{B}, \num{\mu}, \den{\mu}\gets \texttt{frac\_gso}()\\ 2 & k\gets 2\\ 3 & \textbf{while}~k\le n~\textbf{do}\\ 4 & \quad \textbf{for}~j=k-1~\text{downto}~1~\textbf{do}\\ 5 & \quad\quad \texttt{frac\_size}(k, j)\\ 6 & \quad i\gets 1\\ 7 & \quad p\gets 1;~s\gets 0\\ 8 & \quad g\gets \norm{\boldsymbol{b}_k}^2\\ 9 & \quad \textbf{while}~i< k~\textbf{do}\\ 10 & \quad\quad \textbf{if}~\left(bg\den{B_i}-a\num{B_i}\right)p\ge b\den{B_i}s~\textbf{then}\\ 11 & \quad\quad\quad p\gets p\left(\den{\mu_{k, i}}\right)^2\den{B_i}\\ 12 & \quad\quad\quad i\gets i+1\\ 13 & \quad\quad\quad s\gets 0\\ 14 & \quad\quad\quad \textbf{for}~j=1~\text{to}~i-1~\textbf{do}\\ 15 & \quad\quad\quad\quad s\gets s+\frac{p\num{\mu_{k, j}}\num{B_j}}{\left(\den{\mu_{k, j}}\right)^2\den{B_j}}\\ 16 & \quad\quad\textbf{else}\\ 17 & \quad\quad\quad \left\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\right\}\gets \sigma_{i, k}(\left\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\right\})\\ 18 & \quad\quad\quad \texttt{update\_gso\_deep\_insertion}(i, k)\\ 19 & \quad\quad\quad k\gets \max\{i-1, 1\}\\ 20 & \quad k\gets k+1 \end{array} $$
実装には，
前回
同様$\texttt{SageMath}$を用いました．実際のコードは
$\texttt{https://github.com/satoshin-des/fracLLL/blob/e58be6a2b3eeb73919a2afeb4f2aad488d98d985/sage/fracDeepLLL.sage}$
を参照していただくか，本記事の末尾をご覧ください．
$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$を$\texttt{frac\_deep\_lll}$へ入力する$n$次元格子の基底とし，入力した基底に対する$3$行目の$\textbf{while}$文の繰り返し回数を$\mathcal{O}(C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n))$とする．このとき，$\texttt{frac\_deep\_lll}$の計算量は$\mathcal{O}\left(C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)n^3\right)$未満である．
DeepLLLアルゴリズムの計算量は正確にはわかっていません．しかし，実験的に格子次元$n$に関してsuper-exponentialな計算量を有することが知られているので，$\mathcal{O}(C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n))$はsuper-exponentialと仮定しています．
関数fの計算量を$T(\texttt{f})$とします．
前回
の命題5より
$$
\begin{aligned}
T(\texttt{frac\_gso})&=\mathcal{O}(n^5)\\
T(\texttt{frac\_size}(i, j))&=\mathcal{O}(n+j)
\end{aligned}
$$
でした．更に，
$$
\begin{aligned}
T(\texttt{update\_gso\_deep\_insertion}(i, k))&=\mathcal{O}\left(n^2+\sum_{\ell=i+1}^k\left(n+n^2\right)\right)\\
&=\mathcal{O}\left(n^2+(k-i)\left(n+n^2\right)\right)
\end{aligned}
$$
です．従って，
$$
\begin{aligned}
T(\texttt{frac\_deep\_lll})&<\mathcal{O}\left(n^5+C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)\left(\sum_{j=1}^{n-1}(n+j)+n+n^2+(n-1)(n+n^2)+n(n-1)\right)\right)\\
&=\mathcal{O}\left(n^5+C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)\left(n(n-1)+\frac{n(n-1)}{2}+n^2+n^3-n-n^2+n^2-n\right)\right)\\
&=\mathcal{O}\left(n^5+C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)n^3\right)\\
&=\mathcal{O}\left(C(n;\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)n^3\right).\quad \square\\
\end{aligned}
$$
今回は実行時間ではなく，簡約の精度を確かめるために簡約された基底のRHFを比較しました．なお，RHFとは次のように定義される量です．
格子基底$\{\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n\}$のRoot of Hermite factorもしくはRHFとは
$$
\mathrm{hf}(\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)\coloneqq \sqrt[n]{\frac{\norm{\boldsymbol{b}_1}}{\sqrt[n]{\mathrm{vol}(\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)}}}
$$
である．但し，
$$
\mathrm{vol}(\boldsymbol{b}_1,\ldots,\boldsymbol{b}_n)\coloneqq \abs{\det\mqty[\boldsymbol{b}_1\\\vdots\\\boldsymbol{b}_n]}=\prod_{i=1}^n\norm{\boldsymbol{b}_i^\star}
$$
は格子基底の体積（または行列式）である．
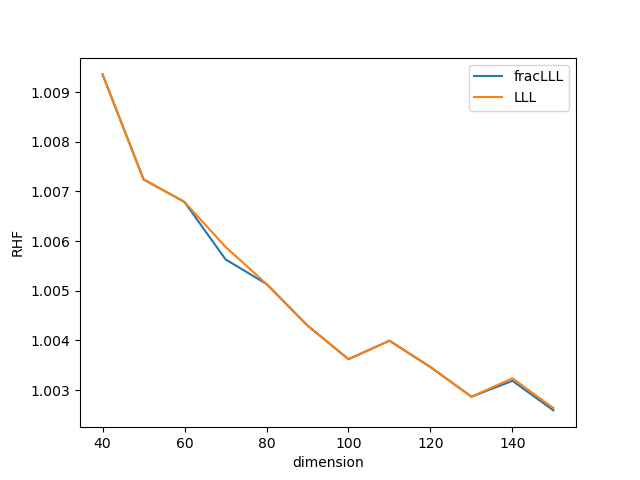"普通の"DeepLLLとfracDeepLLLのRHFの比較
実際のコード
# --------------------
# fracDeepLLL.sage
# --------------------
NUM = 0
DEN = 1
load("fracGSO.sage")
load("fracSize.sage")
def deep_insertion(basis: sage.matrix.matrix_integer_dense.Matrix_integer_dense, i: int, k: int) -> sage.matrix.matrix_integer_dense.Matrix_integer_dense:
"""Apply deep-insertion(i, k) to lattice basis
Args:
basis (sage.matrix.matrix_integer_dense.Matrix_integer_dense): lattice basis
i (int): index
k (int): index
Returns:
sage.matrix.matrix_integer_dense.Matrix_integer_dense: Deep-inserted basis
"""
t = basis[k, :]
for j in xsrange(k, i, -1):
basis[j] = basis[j - 1, :]
basis[i] = t[:]
return basis
def update_gso_deep_insertion(mu: list, B: list, i: int, k: int, n: int) -> tuple:
"""Update Gram-Schmidt orthogonalization information by applying deep-insertion(i, k)
Args:
mu (list): Gram-Schmidt orthogonalization coefficient matrix
B (list): Squared norm of Gram-Schmidt orthogonalization vectors
i (int): index
k (int): index
n (int): lattice rank
Returns:
tuple: Tuple of updated Gram-Schmidt orthogonaliztion informations
"""
C_num = copy(B[NUM])
C_den = copy(B[DEN])
nu_num = copy(mu[NUM])
nu_den = copy(mu[DEN])
for l in xsrange(k, i, -1):
C_num[l - 1] = B[NUM][l] * B[DEN][l - 1] * mu[DEN][l, l - 1] ^ 2 + mu[NUM][l, l - 1] ^ 2 * B[DEN][l] * B[NUM][l - 1]
C_den[l - 1] = B[DEN][l] * B[DEN][l - 1] * mu[DEN][l, l - 1] ^ 2
d = gcd(C_num[l - 1], C_den[l - 1])
C_num[l - 1] //= d
C_den[l - 1] //= d
C_num[l] = B[NUM][l - 1] * B[NUM][l] * C_den[l - 1]
C_den[l] = B[DEN][l - 1] * B[DEN][l] * C_num[l - 1]
d = gcd(C_num[l], C_den[l])
C_num[l] //= d
C_den[l] //= d
nu_num[l, l - 1] = mu[NUM][l, l - 1] * B[NUM][l - 1] * C_den[l - 1]
nu_den[l, l - 1] = mu[DEN][l, l - 1] * B[DEN][l - 1] * C_num[l - 1]
d = gcd(nu_num[l, l - 1], nu_den[l, l - 1])
nu_num[l, l - 1] //= d
nu_den[l, l - 1] //= d
for j in xsrange(l - 1):
nu_num[l - 1, j] = mu[NUM][l, j]
nu_den[l - 1, j] = mu[DEN][l, j]
d = gcd(nu_num[l - 1, j], nu_den[l - 1, j])
nu_num[l - 1, j] //= d
nu_den[l - 1, j] //= d
nu_num[l, j] = mu[NUM][l - 1, j]
nu_den[l, j] = mu[DEN][l - 1, j]
d = gcd(nu_num[l, j], nu_den[l, j])
nu_num[l, j] //= d
nu_den[l, j] //= d
for i in xsrange(l + 1, n):
nu_num[i, l] = mu[NUM][i, l - 1] * mu[DEN][l, l - 1] * mu[DEN][i, l] - mu[NUM][l, l - 1] * mu[NUM][i, l] * mu[DEN][i, l - 1]
nu_den[i, l] = mu[DEN][i, l - 1] * mu[DEN][l, l - 1] * mu[DEN][i, l]
d = gcd(nu_num[i, l], nu_den[i, l])
nu_num[i, l] //= d
nu_den[i, l] //= d
nu_num[i, l - 1] = mu[NUM][i, l] * nu_den[l, l - 1] * nu_den[i, l] + mu[DEN][i, l] * nu_num[l, l - 1] * nu_num[i, l]
nu_den[i, l - 1] = mu[DEN][i, l] * nu_den[l, l - 1] * nu_den[i, l]
d = gcd(nu_num[i, l - 1], nu_den[i, l - 1])
nu_num[i, l - 1] //= d
nu_den[i, l - 1] //= d
B[NUM] = C_num[:]
B[DEN] = C_den[:]
mu[NUM] = nu_num[:, :]
mu[DEN] = nu_den[:, :]
return [C_num, C_den], [nu_num, nu_den]
def frac_deep_lll(basis: sage.matrix.matrix_integer_dense.Matrix_integer_dense, n: int, a: int, b: int) -> sage.matrix.matrix_integer_dense.Matrix_integer_dense:
"""Compute DeepLLL basis without FPA
Args:
basis (sage.matrix.matrix_integer_dense.Matrix_integer_dense): lattice basis
n (int): lattice rank
a (int): numerator of reduction parameter
b (int): denominator of reduction parameter
Returns:
sage.matrix.matrix_integer_dense.Matrix_integer_dense: DeepLLL-reduced basis
"""
B, mu = frac_gso(basis, n)
k = 1
while k < n:
for j in xsrange(k - 1, -1, -1):
basis, mu = frac_size(basis, mu, k, j)
i = 0
prod = 1
sum = 0
g = basis[k].inner_product(basis[k])
while i < k:
if (b * g * B[DEN][i] - a * B[NUM][i]) * prod >= b * B[DEN][i] * sum:
prod *= mu[DEN][k, i] ^ 2 * B[DEN][i]
i += 1
sum = 0
for j in xsrange(i):
sum += mu[NUM][k, j] * B[NUM][j] * prod // (mu[DEN][k, j] ^ 2 * B[DEN][j])
else:
basis = deep_insertion(basis, i, k)
B, mu = update_gso_deep_insertion(mu, B, i, k, n)
if i > 1:
k = i - 1
else:
k = 0
k += 1
return basis
# --------------------
# fracSize.sage
# --------------------
NUM = 0
DEN = 1
def frac_size(basis: sage.matrix.matrix_integer_dense.Matrix_integer_dense, mu: list, i: int, j: int) -> tuple:
"""Size-reduction with rational number representation.
Args:
basis (sage.matrix.matrix_integer_dense.Matrix_integer_dense): Lattice basis.
mu (list): Gram-Schmidt orthogonalization coefficients matrix
i (int): index
j (int): index
Returns:
tuple: Tuple of updated lattice basis and Gram-Schmidt orthogonalization coefficients matrix
"""
if 2 * abs(mu[NUM][i, j]) > abs(mu[DEN][i, j]):
q = ZZ(round(mu[NUM][i, j] / mu[DEN][i, j]))
basis[i] -= q * basis[j]
for l in xsrange(j + 1):
mu[NUM][i, l] = mu[NUM][i, l] * mu[DEN][j, l] - q * mu[DEN][i, l] * mu[NUM][j, l]
mu[DEN][i, l] *= mu[DEN][j, l]
d = gcd(mu[NUM][i, l], mu[DEN][i, l])
mu[NUM][i, l] //= d
mu[DEN][i, l] //= d
return basis, mu
# --------------------
# fracGSO.sage
# --------------------
NUM = 0
DEN = 1
def frac_gso(basis: sage.matrix.matrix_integer_dense.Matrix_integer_dense, n: int) -> tuple:
"""Compute Gram-Schmidt orthogonalization information as rational number
Args:
basis (sage.matrix.matrix_integer_dense.Matrix_integer_dense): Lattice basis
n (int): Rank of lattice
Returns:
tuple: Tuple of Gram-Schmidt orthogonalization informations
"""
G = basis * basis.transpose()
B_num = vector(ZZ, n)
B_den = vector(ZZ, n)
mu_num = identity_matrix(ZZ, n)
mu_den = matrix(ZZ, n, n)
D = matrix(ZZ, n, n)
for i in xsrange(n):
for j in xsrange(n):
mu_den[i, j] = 1
for i in xsrange(n):
for j in xsrange(n):
if (i == 0) and (j == 0):
D[i, j] = 1
else:
d = matrix(ZZ, i, i)
for k in xsrange(i):
if k < j:
d[k] = G[k, : i]
else:
d[k] = G[k + 1, : i]
D[i, j] = d.det()
for i in xsrange(n):
sum = 0
for j in xsrange(i + 1):
for k in xsrange(i + 1):
if ((j + k) & 1) == 0:
sum += D[i, j] * D[i, k] * G[j, k]
else:
sum -= D[i, j] * D[i, k] * G[j, k]
B_num[i] = sum
B_den[i] = D[i, i] * D[i, i]
d = gcd(B_num[i], B_den[i])
B_num[i] //= d
B_den[i] //= d
for j in xsrange(i):
sum = 0
for k in xsrange(j + 1):
if ((j + k) & 1) == 0:
sum += D[j, k] * G[i, k]
else:
sum -= D[j, k] * G[i, k]
mu_num[i, j] = D[j, j] * sum
sum = 0
for k in xsrange(j + 1):
for l in xsrange(j + 1):
if ((k + l) & 1) == 0:
sum += D[j, k] * D[j, l] * G[k, l]
else:
sum -= D[j, k] * D[j, l] * G[k, l]
mu_den[i, j] = sum
d = gcd(mu_num[i, j], mu_den[i, j])
mu_num[i, j] //= d
mu_den[i, j] //= d
return [B_num, B_den], [mu_num, mu_den]
