t分布の性質とF分布の導入
はじめに
今回は$t$分布の諸性質を紹介する.さらに,$F$分布の導入を目指す.
$t$分布のグラフの形を探る
まず,$t$分布の定義を思い出す.
確率変数$W$と$V$が独立で,$W$は標準正規分布に従い,$V$は自由度$r$のカイ二乗分布に従うとき,
$T= \frac{W}{ \sqrt{\frac{V}{r}} } $
は,自由度$r$の$t$分布に従うという.
さらに,このときの$r.v.T$の確率密度関数は
$g_1(t) = \frac{\Gamma[\frac{r+1}{2}]}{\sqrt{\pi r}\Gamma[\frac{r}{2}]} {[1+\frac{t^2}{r}]^\frac{-(r+1)}{2}} (-\infty< t<\infty)$・・・(3.6.2)
とかけるのだった.
これを用いて,$t$分布の確率密度関数のグラフの形状を考える.
1. $g_1(t)$の対称性
まず,直ちに
$g_1(-t)=g_1(t)^{※1}$
が分かる.
したがって,$r.v.T$の確率密度関数は$0$に関して対称である.
(さらに,このことから$T$の中央値が$0$であることも分かる.$^{※2}$)
確率変数Xの中央値とは,
$P(X \geq m) \geq \frac{1}{2}, P(X \leq m) \geq \frac{1}{2}$
を満たす実数$m$.
2. $g_1(t)$の挙動
次に, $g_1(t)$を$t$に関して微分してみると,以下を得る.
$\frac{d}{dt}g_1(t) = \frac{\Gamma[\frac{r+1}{2}]}{\sqrt{\pi r}\Gamma[\frac{r}{2}]}[-\frac{r+1}{r}] t {[1+\frac{t^2}{r}]^\frac{-(r+3)}{2}}$ $ (-\infty< t<\infty)$
符号を司る部分は
$-t {[1+\frac{t^2}{r}]^\frac{-(r+3)}{2}}$
だが,括弧部は常に正ゆえ,実際に着目すべきは$-t$のみ.
したがって,$g_1(t)$は$t=0$で唯一の最大値をとることが分かる.
同時に,$\frac{d}{dt}g_1(t)$の連続性も加味する.
結論:$g_1(t)$のグラフの概形
よって,$t$分布の確率密度関数のグラフの形状は以下のようと分かる.
![[-4,4]で描いた自由度3のt分布のグラフ](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FCmZxWetVGkdHNsFBCif8.png?alt=media) [-4,4]で描いた自由度3のt分布のグラフ
[-4,4]で描いた自由度3のt分布のグラフ
描画に用いたRのコードは後述.
$t$分布の諸性質
正規近似
まず,$t$分布の重要な性質を紹介する.
$t$分布は,自由度$r \rightarrow \infty $のとき,標準正規分布に近づく.
(3.6.2)式で書ける確率密度関数が,$r \rightarrow \infty $のとき,標準正規分布のそれと等しくなることを言えばよい.
まず,$r \rightarrow \infty $のとき,
${[1+\frac{t^2}{r}]^\frac{-(r+1)}{2}} = {[(1+\frac{t^2}{r})^r}]^\frac{-1}{2}(1+\frac{t^2}{r})^\frac{-1}{2} \rightarrow \exp(\frac{-t^2}{2}) ^{※3}$
次に,スターリングの公式(下に記載)を用いると,十分大きな$r$に対して
$\frac{\Gamma[\frac{r+1}{2}]}{\Gamma[\frac{r}{2}]} = [\frac{r}{2}]^\frac{1}{2}$
が成り立つ.
以上より,$r \rightarrow \infty $で
$g_1(t) = \frac{\Gamma[\frac{r+1}{2}]}{\sqrt{\pi r}\Gamma[\frac{r}{2}]} {[1+\frac{t^2}{r}]^\frac{-(r+1)}{2}} \rightarrow \frac{1}{\sqrt{2\pi}}\exp[-\frac{t^2}{2}]$
と分かり,題意を得る.
$x \rightarrow \infty $のとき$\frac{\Gamma[x+y]}{\Gamma[x]} \rightarrow x^y$
平均と分散(Example3.6.1)
$r.v.T$が自由度$r$の$t$分布に従うとき,
$E[T] = 0(r \gt 1)$
$Var[T] = \frac{r}{r-2} (r \gt 2)$
①準備
まず,$t$分布の定義より,標準正規分布に従う$r.v.W$と,自由度$r$のカイ二乗分布に従う$r.v.V$($W$と$V$は独立とする)を用いて
$T=\frac{W}{\sqrt{V/r}}$
とかける.
$W$と$V$の独立性から,
$\begin{eqnarray} E[T^k] &=& E[W^k(\frac{V}{r})^{-k/2}] = E[W^k]E[(\frac{V}{r})^{-k/2}]\\ &=& E[W^k]\frac{1}{r^{-k/2}}E[V^{-k/2}] \end{eqnarray}$
ここに,(3.3.8)式(下に記載)から得られる
$E[V^{-k/2}] = 2^{-k/2} \frac{\Gamma[\frac{r}{2}-\frac{k}{2}]}{\Gamma[\frac{r}{2}]} (-k/2 \gt -r/2)$
を代入すると,
$E[T^k] = E[W^k]\frac{2^{-k/2} \Gamma[\frac{r}{2}-\frac{k}{2}]}{\Gamma[\frac{r}{2}]r^{-k/2}} (k \lt r)$・・・(3.6.4)
②平均を求める
$r.v.W$の定義から$E[W] = 0$ゆえ,
$E[T] = 0(r>1)$
③分散を求める
$T$の平均が$0$であることから,
$\begin{eqnarray}
Var[T] &=& E[T^2] - E[T]^2 \\
&=&E[T^2] \\
&=& \frac{r}{r-2}(r>2) ^{※4}
\end{eqnarray}$
確率変数$X$が自由度$r$のカイ二乗分布に従うとき,
$E[X^k] = 2^k \frac{\Gamma[\frac{r}{2}+k]}{\Gamma[\frac{r}{2}]} (k \gt -r/2)$・・・(3.3.8)
n$\geq$1の整数に対して, $\alpha>0$ならば
$\Gamma[\alpha+n]=(\alpha+n-1)\cdots(\alpha+1)\alpha\Gamma(\alpha)$
コーシー分布
平均が定義されない$r=1$の場合の分布は,標準コーシー分布と同じ.
$f_X(x) = \frac{1}{\pi(x^2+1)}$
$t$分布がらみのRコマンド
先ほどの図1を描くのに用いたコードは以下.
 グラフ描画
グラフ描画
数列tを生成した後,それを自由度$3$の$t$分布の確率密度関数に代入した値との組をプロットしている.
また,以下の2つのコマンドも有用である.
 その他のコマンド
その他のコマンド
上段では,$T$が自由度$15$の$t$分布に従うときの$P(T \leq 2.0)$の値が,
下段では,自由度$15$の$t$分布の下側確率$97.5$%点が,それぞれ返却されている.
$t$分布表
これまで見てきたように,$t$分布は自由度$r$にのみ依存する.
つまり,自由度を定めれば,各パーセント点が与えられる.
これを用いて,$t$分布表が作られている.
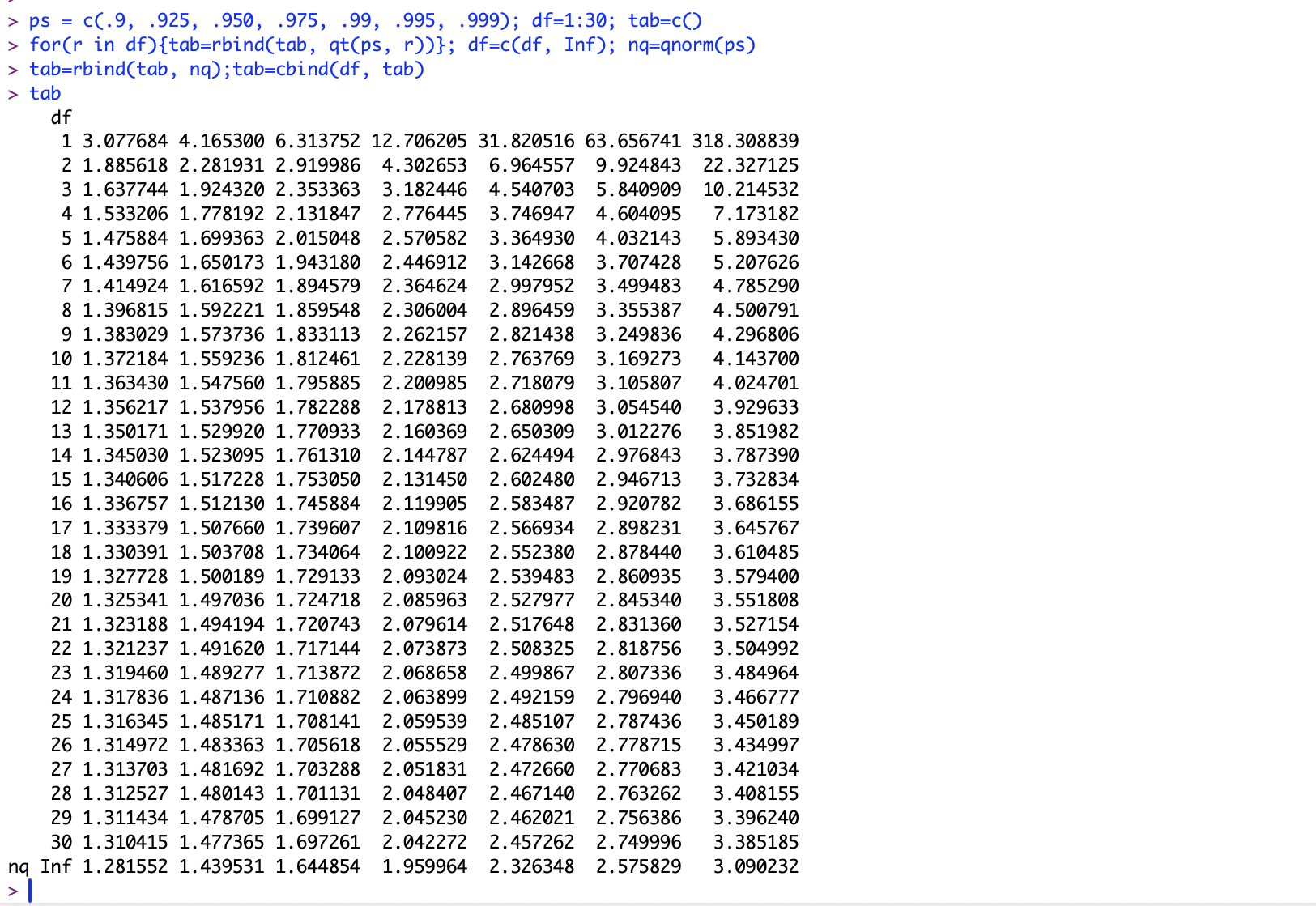 Rで作るt分布表
Rで作るt分布表
補足(Remark3.6.1)
$t$分布は,発明したW.S.Gossetのペンネームから,Studentの$t$分布とも呼ばれる.
$F$分布の導入
ここでは,$F$分布の定義と確率密度関数の導出を行う.
確率変数$U$と$V$が独立で,$U$は自由度$r_1$のカイ二乗分布に従い,$V$は自由度$r_2$のカイ二乗分布に従うとき,
$W= \frac{U/r_1}{V/r_2} $
は,自由度$r_1,r_2$の$F$分布に従うという.
このときの$r.v.W$の確率密度関数は
$g_1(w) = \begin{eqnarray} \left\{ \begin{array}{l} \frac{\Gamma[\frac{r_1+r_2}{2}](r_1/r_2)^{r_1/2}}{\Gamma[\frac{r_1}{2}]\Gamma[\frac{r_2}{2}]} \frac{w^{r_1/2-1}}{(1+r_1w/r_2)^{(r_1+r_2)/2}} &0< w<\infty \\ 0&elsewhere. \end{array} \right. \end{eqnarray} $ ・・・(3.6.6)
とかける.$F$分布は,パラメータ$r_1$および$r_2$から決まる.
補足
確率変数を$W$でなく$F$で表すことも多い.
確率密度関数の導出
最後に,(3.6.6)式の導出を行う.
定義にあるように,確率変数$U,V$および$W$を定めるとき,$U$と$V$の結合確率密度関数は
$h(u,v) = \begin{eqnarray} \left\{ \begin{array}{l} \frac{1}{\Gamma[\frac{r_1}{2}]\Gamma[\frac{r_2}{2}] 2^{(r_1+r_2)/2}} u^{r_1/2-1}v^{r_2/2-1}e^{-(u+v)/2}&0< u,v<\infty \\ 0&elsewhere. \end{array} \right. \end{eqnarray}^{※5} $
求める$W$の確率密度関数を$g_1(w)$とし,変数変換
$w=\frac{u/r_1}{v/r_2}, z=v$
を考えると,$(u,v)$と$(w,z)$とは一対一に対応し,
$ \mathcal{S} = \{(u, v):0< u<\infty,0< v<\infty\}$
は
$ \mathcal{T} = \{(w, z):0< w<\infty,0< z<\infty\}$
に写る.
また,
$u=\frac{r_1}{r_2}zw, v=z ^{※6}$ゆえ,ヤコビアンを計算すると
$|J| = (r_1/r_2)z ^{※7}$
以上より,$W$と$Z$の結合確率密度関数は
$g(w,z) = \begin{eqnarray} \left\{ \begin{array}{l} \frac{1}{\Gamma[\frac{r_1}{2}]\Gamma[\frac{r_2}{2}] 2^{(r_1+r_2)/2}}(\frac{r_1zw}{r_2})^{(r_1-2)/2}z^{(r_2-2)/2}exp[-\frac{z}{2}(\frac{r_1w}{r_2}+1)]\frac{r_1z}{r_2} &(w,z) \in \mathcal{T} \\ 0&elsewhere. \end{array} \right. \end{eqnarray}^{※8} $
したがって,$W$の周辺確率密度関数は
$\displaystyle\begin{eqnarray}
g_1(w)
&=&
\int_{-\infty}^{\infty} g(w,z)dz\\
&=&
\int_{0}^{\infty} \frac{(r_1/r_2)^{r_1/2}(w)^{r_1/2-1}}{\Gamma[\frac{r_1}{2}]\Gamma[\frac{r_2}{2}] 2^{(r_1+r_2)/2}}z^{(r_1+r_2)/2-1}exp\Big[-\frac{z}{2}\Big(\frac{r_1w}{r_2}+1\Big)\Big]dz
\end{eqnarray}
^{※9}
$
さいごに,
$y=\frac{z}{2}(\frac{r_1w}{r_2}+1)$
とおけば,
$\displaystyle\begin{eqnarray}
g_1(w)
&=&
\int_{0}^{\infty} \frac{(r_1/r_2)^{r_1/2}(w)^{r_1/2-1}}{\Gamma[\frac{r_1}{2}]\Gamma[\frac{r_2}{2}] 2^{(r_1+r_2)/2}}\Big(\frac{2y}{r_1w/r_2+1}\Big)^{(r_1+r_2)/2-1}e^{-y}\Big(\frac{2}{r_1w/r_2+1}\Big)dy\\
\\
&=&
\left\{
\begin{array}{l}
\frac{\Gamma[\frac{r_1+r_2}{2}](r_1/r_2)^{r_1/2}}{\Gamma[\frac{r_1}{2}]\Gamma[\frac{r_2}{2}]} \frac{w^{r_1/2-1}}{(1+r_1w/r_2)^{(r_1+r_2)/2}} &0< w<\infty
\\
0&elsewhere.
\end{array}
\right.
\end{eqnarray}
$
以下は補足
歪度と尖度
上で求めた平均と分散を用いて,歪度と尖度を求める.
$t$分布の歪度は$0$(ただし$r>3$)
$t$分布の尖度は$\frac{6}{r-4}$(ただし$r>4$)
以下,定義にあるように,確率変数$T,W,V$を定め,$T$の平均を$\mu$,分散を$\sigma^2$とする.
先に示した通り,$\mu=0(r>1),\sigma^2=\frac{r}{r-2}(r>2)$
下の定理を用いると,歪度と尖度はそれぞれ
$\frac{E[(T-\mu)^3]}{\sigma^3}=\frac{E[T^3]}{\sigma^3}=\frac{1}{\sigma^3}E[W^3](\frac{r}{2})^{3/2}\frac{\Gamma[(r-3)/2]}{\Gamma[r/2]}^{※10}=0(r>3)$
$\frac{E[(T-\mu)^4]}{\sigma^4}-3=\frac{E[T^4]}{\sigma^4}-3=\frac{1}{\sigma^4}E[W^4](\frac{r}{2})^{2}\frac{\Gamma[(r/2)-2]}{\Gamma[r/2]}^{※11}-3=\frac{6}{r-4}(r>4)$
確率変数$X$が標準正規分布に従うとき,$X$の中心積率は
$E[X^m]=\begin{eqnarray}
\left\{
\begin{array}{l}
(2k-1)\cdots5\cdot3\cdot1
&(m=2k, k=1,2,3,...)
\\
0&otherwise.
\end{array}
\right.
\end{eqnarray}
$
定理4より
$t$分布の尖度は,自由度$r$が大きいほど小さくなることがわかる.
さらに,自由度$r$を十分大きくすると尖度が$0$に収束することから,このときの分布は正規分布とみなすことができる.
