解析概論 練習問題 解答 1章～3章

$a_n>b_n>0$と仮定すると$a_{n+1}=\dfrac12(a_n+b_n)<\dfrac12(a_n+a_n)=a_n,$ $b_{n+1}=\sqrt{a_nb_n}>\sqrt{b_n^2}=|b_n|=b_n>0,$ $a_{n+1}-b_{n+1}=\dfrac12(\sqrt{a_n}-\sqrt{b_n})^2>0$より$a_n>a_{n+1}>b_{n+1}>b_n>0$から帰納的に$a_1>\cdots>a_n>\cdots>b_n>\cdots>b_1>0$。単調収束定理より$a_n\to\alpha,\ b_n\to\beta$とできる。$a_n=\dfrac{1}{2}\q(a_{n-1}+b_{n-1})$より$\alpha=\dfrac12\q(\alpha+\beta)$から$\alpha=\beta$。

$a_1=b_1$であれば明らか。$b_1>0$である。$a_1>b_1$のとき、$a_n>b_n>0$とすると$a_{n+1}< a_n,\ b_{n+1}=\sqrt{a_{n+1}b_n}=\sqrt{\dfrac{a_nb_n+b_n^2}2}>b_n>0$より問題1と同様にして示される。

1. このとき$a_1=\dfrac {b(1+\cos x)}2=b\cos^2\dfrac{x}2,\ b_1=b\cos\dfrac x2$。帰納法により$a_n=b_n\cos\dfrac x{2^n},b_n=b\displaystyle\prod_{k=1}^n\cos\dfrac x{2^k}$を示す。これを仮定すると
   \begin{align} b_{n+1}&=b_n\sqrt{\dfrac12\q(1+\cos\dfrac{x}{2^n})}=b_n\cos\dfrac{x}{2^{n+1}}=b\displaystyle\prod_{k=1}^{n+1}\cos\dfrac x{2^k},\\ a_{n+1}&=\dfrac{b_n}2\q(1+\cos\dfrac{x}{2^n})=\dfrac{b_n}2\cos^2\dfrac{x}{2^{n+1}}=b_{n+1}\cos \dfrac x{2^{n+1}} \end{align}
   より示すべきは$\displaystyle \prod_{k=1}^\infty\cos\dfrac x{2^k}=\dfrac{\sin x}x$。
   \begin{align} \sin\frac{x}{2^n}\prod_{k=1}^n\cos\dfrac x{2^k}&=\frac12 \sin\frac{x}{2^{n-1}}\prod_{k=1}^{n-1}\cos\dfrac x{2^k}\\ &=\cdots\\ &=\frac{1}{2^n}\sin x \end{align}
   より
   \begin{align} \prod_{k=1}^n\cos\dfrac x{2^k}&=\frac{\sin x}x\cdot \q(\frac {2^n}x\sin\frac x{2^n})^{-1}\to\frac{\sin x}x \end{align}
   から示される。
2. (1)と同様に示される。

$n>N$のとき、$\displaystyle a_n\leq\sup_{n>N}a_n,\ b_n\leq\sup_{n>N}b_n$から$\displaystyle a_n+b_n\leq\sup_{n>N}a_n+\sup_{n>N}b_n$。左辺の上界をとって、$\displaystyle \sup_{n>N}(a_n+b_n)\leq\sup_{n>N}a_n+\sup_{n>N}b_n$。$N\to\infty$として示される。下極限については$-a_n,-b_n$について考えればよい。

$a=\dfrac pq\in\mathbb{Q}$のとき、$\ve=\dfrac1q$とすると、任意の$\delta>0$に対して$\delta>\dfrac{\sqrt2}{N}$なる$N$をとり$x=a+\dfrac{\sqrt{2}}N$と定める。このとき$|x-a|=\dfrac{\sqrt{2}}N<\delta$だが$|f(x)-f(a)|=\dfrac1q\geq\ve$となるから$f(x)$は$x\in\mathbb{Q}$で不連続。
$a\in\mathbb{R}\setminus\mathbb{Q}$のとき、$\ve>0$に対して$\ve>\dfrac{1}N$となるような$N$を1つとり、$\delta=\displaystyle\min_{1\leq k\leq n\leq N}\q|a-\dfrac kn|$とすると$|x-a|<\delta\Rightarrow |f(x)-f(a)|=|f(x)|<\dfrac1N<\ve$より$f(x)$は$x\in\mathbb{R}\setminus\mathbb{Q}$で連続。

稠密の定義より$x\in[a,b]\setminus I$は$x=\lim x_n,\ x_n\in I$と表される。仮定より$f(x_n)=g(x_n)$で、$f,g$は$[a,b]$上連続だから両辺極限を取って$f(x)=g(x)$

$\hat{f}$が存在する$\iff f$が$I$上一様連続
であることを示す。

$(\Longleftarrow)$ $\q{x_n}\subset I$がCauchy列$\Longrightarrow$ $\q{f(x_n)}$がCauchy列を示す。$f$が$I$上一様連続だから、$\ve>0$に対し、ある$\delta>0$があって$|x-x'|<\delta\Rightarrow|f(x)-f(x')|<\ve$。$\q{x_n}$がCauchy列だからある$N$があって$n,m>N$ならば$|x_n-x_m|<\delta$なるように$N$をとれる。このとき、$n,m>N$ならば$|f(x_n)-f(x_m)|<\ve$となるから、$\q{f(x_n)}$もCauchy列。よって、$\q{f(x_n)}$は収束するから、
$\hat{f}(x)= \begin{eqnarray} \left\{ \begin{array}{l} f(x)\quad&(x\in I) \\ \lim f(x_n)&(x=\lim x_n\in[a,b]\setminus I,\ x_n\in I) \end{array} \right. \end{eqnarray} $が定まる。$\lim x_n=\lim x'_n$に対して$\lim f(x_n)=\lim f(x'_n)$を示す。$\lim f(x_n)\ne\lim f(x'_n)$とすると、$x''_{2n}=x_n,\ x''_{2n+1}=x'_n$に対して$x''_n$もまたCauchy列だが$\lim f(x''_n)$は収束せず$\q{f(x''_n)}$がCauchy列であることに反する。よって$\hat{f}(x)$はwell-defined。
$\hat{f}(x)$が$[a,b]$上連続であることを示す。任意の$\ve>0$をとり、任意の$n\in\mathbb{N}$に対して$|\hat{f}(\lambda_n)-f(\lambda'_n)|<\ve$を満たすような$\q{\lambda'_n}\subset I,\ \lambda_n'\to\lambda$をとる。($\q{\mu_{n,m}}\subset I,\ \ds\lim_{m\to\infty}\mu_{n,m}=\lambda_n$なる$\mu_{n,m}$をとると、$\ds\lim_{m\to\infty}f(\mu_{n,m})=\hat{f}(\lambda_n)$よりある$M$があって$m>M$ならば$|\hat{f}(\lambda_n)-f(\mu_{n,m})|<\ve$とできる。よって、$\lambda_n'=\mu_{n,M+1}$とすればよいから、このような$\lambda_n'$は存在する。)$\lambda_n'\to\lambda$だから、$|\hat{f}(\lambda_n)-f(\lambda'_n)|<\ve$より$|\lim \hat{f}(\lambda_n)-\hat{f}(\lambda)|<\ve$。$\ve$は任意だから、$\lim\hat{f}(\lambda_n)=\hat{f}(\lambda)$、つまり$\hat{f}$は連続。
$(\Longrightarrow)$ Heine-Cantorの定理より、$\hat{f}$は一様連続。つまり、$\forall \ve>0, \exists \delta>0, \forall x,x'\in[a,b]:\ |x-x'|<\delta\Longrightarrow |\hat{f}(x)-\hat{f}(x')|<\ve$だから、$x\in I$で$f(x)=\hat{f}(x)$より$\forall \ve>0, \exists \delta>0, \forall x,x'\in I:\ |x-x'|<\delta\Longrightarrow |f(x)-f(x')|<\ve$より$f$も一様連続。

$f(x)-lx$を考えることにより$l=0$としてよい。 $\ds\lim_{x\to\infty} (f(x+1)-f(x))=0$より、任意の$\ve>0$に対しある$L$があって$x>L$ならば$|f(x+1)-f(x)|<\dfrac\ve2$。$x$を十分大きくとって$n=\lfloor x\rfloor-L$とすれば$L\leq x-n< L+1$より
\begin{align} |f(x)|&=\q|\sum_{k=0}^{n-1} (f(x-k)-f(x-k-1))+f(x-n)|\\ &\leq \sum_{k=0}^{n-1} |f(x-k)-f(x-k-1)|+|f(x-n)|\\ &\leq \dfrac{n\ve}2+|f(x-n)|\\ &\leq\dfrac{x\ve}2+|f(x-n)| \end{align}
$[L,L+1]$における$|f(x)|$の最大値を$M$とすると、$x>\dfrac{2M}\ve$のとき
\begin{align} \q|\dfrac{f(x)}x|\leq\dfrac{\ve}{2}+\dfrac{M}x<\ve \end{align}
より示される。

$a\in K$を任意にとる。$g$が連続だから任意の$\ve>0$に対しある$\delta>0$があって$|y-f(a)|<\delta\Longrightarrow|g(y)-g(f(a))|<\ve$。$g\circ f$を考えるから$y=f(x)$とおけるとしてよく、このとき$|f(x)-f(a)|\Longrightarrow |g(f(x))-g(f(a))|<\ve$。$f$が連続だからある$\delta'$があって$|x-a|\Longrightarrow |f(x)-f(a)|<\delta$。よって$|x-a|<\delta'\Longrightarrow |g(f(x))-g(f(a))|<\ve$から$g\circ f$は連続。

$x,y$に収束する$\q{x_n},\q{y_n}\subset \QQ$をとると、$(a^{x_n})^{y_n}=a^{x_ny_n}$より、$a^u,\ u\in\QQ$の連続性より両辺極限とって示される。

$\varphi(t)=\dfrac{1}{t}+a-1$とすると$\varphi((0,1])=[a,\infty)$。$g=f\circ \varphi:(0,1]\to\RR$を$g(0)=g(1)$として$g$の定義域を拡張すると$\ds\lim_{t\to+0}g(t)=\lim_{x\to\infty}f(t)=f(a)=f(\varphi(1))=g(1)=g(0)$より$g$は$[0,1]$で連続。Rolleの定理よりある$\xi\in (0,1)$があって$g'(\eta)=f'(\varphi(\eta))\varphi'(\eta)=0$、よって$f'(\varphi(\eta))=0$。$\varphi(\eta)>a$から$\xi=\varphi(\eta)$とすればよい。

$P_1(x)=-2ax$であり、$P_n(x)$が$n$次の多項式であるとすると
\begin{align} \dvn{x}{n+1}\dfrac1{(1+x^2)^a}=\dv{x}\dfrac{P_n(x)}{(1+x^2)^{a+n}}=\dfrac{(1+x^2)P_n'(x)+P_n(x)}{(1+x^2)^{a+n+1}} \end{align}
より$P_{n+1}(x)=(1+x^2)P_n'(x)+P_n(x)$から$P_{n+1}(x)$は$n+1$次の多項式。よって帰納法から示される。
$f(x)=\dfrac{P_n(x)}{(1+x^2)^{a+n}}$とすると、$P_n(x)$と$f(x)$の根は一致する。$f^{(0)}(x)=\dfrac1{(1+x^2)^a},\ f^{(1)}(x)=\dfrac{-2ax}{(1+x^2)^{a+1}}$より$f^{(0)}(x)とf^{(1)}(x)$の根は全て異なる。$f^{(n)}(x)$が$\lambda_1<\cdots<\lambda_n$なる$n$個の根を持つとする。$f^{(n+1)}(\lambda_i)=\dfrac{P_n'(\lambda_i)}{(1+\lambda_i^2)^{a+n}}$であり、$\lambda_i$は$P_n(x)$の根で、$P_n(x)$は重解を持たないから$P_n'(\lambda_i)\ne0$。また、$1\leq i\leq n-1$で$P_n'(\lambda_i)<0$とすると$P_n'(\lambda_{i+1})>0$であり、$P_n'(\lambda_i)>0$とすると$P_n'(\lambda_{i+1})<0$であるから中間値の定理より$\lambda_i<\mu_i<\lambda_{i+1}$なる$\mu_i$があって$f^{(n+1)}(\mu_i)=0$。また、$\ds\lim_{x\to\pm\infty}f^{(n)}(x)=0=f^{(n)}(\lambda_1)=f^{(n)}(\lambda_n)$から問題1より$\mu_0<\lambda_1,\ \lambda_n<\mu_n$なる$\mu_0,\ \mu_n$があって$f^{(n+1)}(\mu_0)=f^{(n+1)}(\mu_n)=0$。よって、$f^{(n+1)}$は相異なる根$\mu_0<\cdots<\mu_n$を持ち、それらはいずれも$\lambda_i$とは一致しない。

前問題と同様。

$f_+^{(1)}(a)=l_1$のみ示せば同様の議論を繰り返すことができ示される。
$f(a)=l$とすれば$f(x)$は$[a,b)$で連続、$(a,b)$で微分可能より平均値の定理から
\begin{align} \dfrac{f(x)-f(a)}{x-a}=f'(\xi),\qquad a<\xi< x \end{align}
なる$\xi$がとれる。$x\to a+0$で$\xi\to a+0$から$f'_+(a)=l_1$。

$h,k\in\RR,\ (u,v)\in D,\ (u,v)\ne(a,b)$に対し$\Delta=f(u+h, v+k)-f(u+h,v)-f(u,v+k)+f(u,v)$と定める。$\vphi(x)=f(x, v+k)-f(x,v)$とすると、$\Delta=\vphi(u+h)-\vphi(u)$。$f_x$の存在より$\vphi(x)$は$[0,h]$で微分可能だから平均値の定理より$0<\theta<1$で
\begin{align} \Delta=h\vphi'(u+\theta h)=h\q(f_x\q(u+\theta h, v+k)-f_x\q(u+\theta h, v)) \end{align}
$f_{xy}$の存在より、平均値の定理から、ある$0<\theta'<1$があって$\dfrac{\Delta}{hk}=f_{xy}(u+\theta h, v+\theta' k)$。よって $h,k\to0$で$\dfrac{\Delta}{hk}\to f_{xy}(u,v)$。また、
\begin{align} \dfrac{\Delta}{hk}=\frac1h\q(\frac{f(u+h,v+k)-f(u+h,v)}{k}-\frac{f(u,v+k)-f(u,v)}k) \end{align}
において、$f_y$の存在より平均値の定理からある$ 0<\eta<1$があって
\begin{align} \dfrac{\Delta}{hk}=\frac{f_y(u+h, v+\eta k)-f_y(u,v+\eta k)}h \end{align}
$k\to0$として、左辺は$\dfrac{f_y(u+h,v)-f_y(u,v)}h$であるから、$h\to0$とすることで、$\dfrac{\Delta}{hk}\to f_{xy}(u,v)$より$f_{yx}$は存在し、$f_{xy}(u,v)=f_{yx}(u,v)$。 $(u,v)$は任意の$D\setminus\q{(a,b)}$の点だから$\ds\lim_{y\to b}f_{xy}(a,y)=\lim_{y\to b}f_{yx}(a,y),\ \lim_{x\to a}f_{xy}(x,b)=\lim_{x\to a}f_{yx}(x,b)$が成立する。
また、この極限が存在するとき、$g(y)=f_x(a,y)$とすればこれは定理23の仮定を満たすから題意が示される。

\begin{align} f_x(x,y)&=2x\Arctan \frac yx-y\\ f_y(x,y)&=-2y\Arctan \frac xy+x\\ f_{xx}(x,y)&=2\Arctan \frac yx-\dfrac{2xy}{x^2+y^2}\\ f_{yy}(x,y)&=-2\Arctan \frac xy+\dfrac{2xy}{x^2+y^2}\\ f_{xy}(x,y)&=f_{yx}(x,y)\\ &=\dfrac{x^2-y^2}{x^2+y^2} \end{align}
より
\begin{align} f_{xx}(0,0)=\lim{x\to0}f_{xx}(x,0)=0 f_{yy}(0,0)=\lim{y\to0}f_{yy}(0,y)=0 \end{align}
また、$f_{xy}$において$(x,y)^{\top}=r (\cos\theta,\sin\theta)^\top$とすると$(x,y)\to(0,0)$で$f_{xy}(x,y)=\cos2\theta$となるから $f_{xy}$は$(0,0)$で不連続。

$F(x)=f(g(x))$とする。$M>N>n$として、Taylorの定理より、$x\to a$で
\begin{align} F(x)-F(a)&=\sum_{n=1}^N \frac{F^{(n)}(a)}{n!}(x-a)^n+o(|x-a|^N)\tag{1}\\ &=\sum_{k=1}^N \frac{f^{(k)}(g(a))}{k!}(g(x)-g(a))^k + o(|x-a|^N)\\ &=\sum_{k=1}^N \frac{f^{(k)}(g(a))}{k!}\q(\sum_{m=1}^M \frac{g^{(m)}(a)}{m!}\q(x-a)^m +o\q(|x-a|^M))^k+o(|x-a|^N)\\ &=\sum_{k=1}^N \frac{f^{(k)}(g(a))}{k!}\q(\sum_{m=1}^M \frac{g^{(m)}(a)}{m!}\q(x-a)^m)^k+o\q(|x-a|^M)+o(|x-a|^N)\\ &=\sum_{k=1}^N \frac{f^{(k)}(g(a))}{k!}\sum_{\substack{i_1+\cdots+i_k=k\\i_1,\cdots,i_k\geq0}}\frac{k!}{i_1!\cdots i_k!} (x-a)^{1\cdot i_1+\cdots+k\cdot i_k}\prod_{j=1}^k\q(g^{\q(j)}\q(a))^{i_j}+o(|x-a|^N)\tag{2} \end{align}
より、式(1)と式(2)の$(x-a)^{n}$の係数を比較すると、
\begin{align} \frac{F^{(n)}(a)}{n!}&=\sum_{k=1}^N \frac{f^{(k)}(g(a))}{k!}\sum_{\substack{i_1+\cdots+i_k=k\\1\cdot i_1+\cdots+k\cdot i_k=n\\i_1,\cdots,i_k\geq0}}\frac{k!}{i_1!\cdots i_k!}\prod_{j=1}^k\q(g^{\q(j)}\q(a))^{i_j}\\ &=\sum_{k=1}^n \sum_{\substack{i_1+\cdots+i_k=k\\1\cdot i_1+\cdots+k\cdot i_k=n\\i_1,\cdots,i_k\geq0}}\frac{1}{i_1!\cdots i_k!}f^{(k)}(g(a))\prod_{j=1}^k\q(g^{\q(j)}\q(a))^{i_j}\\ &=\sum_{\substack{1\cdot i_1+\cdots+n\cdot i_n=n\\i_1,\cdots,i_n\geq0}}\frac{1}{i_1!\cdots i_k!}f^{(i_1+\cdots+i_n)}(g(a))\prod_{j=1}^k\q(g^{\q(j)}\q(a))^{i_j} \end{align}

まず根が1つであることを示す。中間値の定理より根は少なくとも1つ存在する。根が2つ以上あったとし、そのうち2つを$c_1,c_2,f(c_1)=f(c_2)=0$とする。このとき、Rolleの定理より$c_1< d< c_2, f'(d)=0$なる$d$が存在する。$d< x$で$f'(x)>0$、つまり$f(x)$が単調増加となり、$d< b$より$f(d)=0< f(b)$となり矛盾。よって根はただ1つ。それを$\xi$とする。
$a\leq t<\xi$ならば$f'(t)<0$を示す。$f'(t)=0$とすると$f''(x)>0$に反する。$f'(t)>0$とすると、$f''(x)>0$から$x\in[t,b]$で常に$f'(x)>0$、$a< t<\xi$より$f(t)>0$だから$f(b)>0$となり矛盾。よって$f'(t)<0$。
$(a_n, f(a_n))$における$y=f(x)$の接線の$x$切片は$y=xf'(a_n)-a_nf'(a_n)+f(a_n)$$x=a_{n+1}=a_n-\dfrac{f(a_n)}{f'(a_n)}$である。いま平均値の定理よりある$a< e< b$が$f(x)-f(a)=(x-a)f'(e)$を満たすが、$f''(x)>0$より$f(x)-f(a)>(x-a)f'(a)$、よって$f(x)>(x-a_n)f'(a_n)+f(a_n)$から$f(a_{n+1})>(a_{n+1}-a_n)f'(a_n)+f(a_n)=0=f(\xi)>(\xi-a_n)f'(a_n)+f(a_n)$。いま$a\leq a_n<\xi$ならば$y=(x-a_n)f'(a_n)+f(a_n)$は$x$について単調減少だから$a< a_n< a_{n+1}<\xi$。帰納的に$a< a_1<\cdots< a_n<\cdots<\xi$だから$a_n$は収束し、収束値を$\lambda$とすると$\lambda=\lambda-\dfrac{f(\lambda)}{f'(\lambda)}$より$f(\lambda)=0$、つまり$\lambda=\xi$。

$P,Q$は共通因数を持たないとして一般性を失わない。$[a,b]$で常に$Q(x)\ne0$とすると$(a,b)$で$f(x)$は連続だから$x=m$で最小値$f(m)$をとる。明らかに$m\ne a,b$だからこれは$(a,b)$で極値を持たないことに反する。よってある$c\in[a,b]$があって$Q(c)=0$。$P(c)=0$とすると因数定理より共通因数を持たないことに反するから$P(c)\ne0$。$Q(x)=0$なる$x=c_1,\cdots,c_n$をとる。$n=1$のとき、$a< x< c$で$f'(x)<0$、$c< x< b$で$f'(x)>0$より$f(x)\to-\infty$。$n>1$のとき、$I_0=(a,c_1),I_1=(c_1,c_2),\cdots,I_{n-1}=(a_{n-1},a_n),I_n=(a_n,b)$に対し$x\in I_k$ならば$f'(x)<0$だが$x\in I_{k+1}$ならば$f'(x)>0$なるような$k$が少なくとも1つ存在するから、$n=1$のときと同様に$c=c_{k+1}$とすれば$f(x)\to-\infty,\ $

1. \begin{align} &f_x=4x^3+12xy^2,f_y=4y^3+12x^2y-4y,\\ &f_{xx}=12x^2+12y^2,f_{xy}=24xy,f_{yy}=12y^2+12x^2-4 \end{align}
   より$\Delta(x,y)=f_{xx}f_{yy}-f_{xy}^2$とすると$f_x(x,y)=0\iff x=0 \lor x^2+3y^2=0$、$f_y(x,y)=0\iff y=0\lor 3x^2+y^2=1$。よって停留点は$(0,0),(0,\pm1)$。$\Delta(0,0)=0,\Delta(0,\pm1)=96>0$であり、$f_{xx}(0,\pm1)=12>0$より$(0,\pm1)$で極小となる。また、$f(x,0)=x^4,\ f(0,y)=y^2(y+\sqrt2)(y-\sqrt2)$から$(0,0)$の近傍で$f(x,y)$は正にも負にもなりうるから極値をとらない。よって$(0,\pm1,-1)$のみ。

$A(x_1,y_1), B(x_2,y_2),C(x_3,y_3)$とする。平面上の点を$P(x,y)$とすると、距離の和は$f(x,y)=\ds\sum_{i=1}^3\sqrt{(x-x_i)^2+(y-y_i)^2}$だから、$P\ne A,B,C$のとき$f$が極値を持つ必要条件は
$ \begin{eqnarray} \left\{ \begin{array}{l} \ds\frac{\partial f}{\partial x}=\sum_{i=1}^3\frac{x-x_i}{\sqrt{(x-x_i)^2+(y-y_i)^2}}=0 \\ \ds\frac{\partial f}{\partial y}=\sum_{i=1}^3\frac{y-y_i}{\sqrt{(x-x_i)^2+(y-y_i)^2}}=0 \end{array} \right. \end{eqnarray}\qquad\ (1)$
であるが、$\bm{v}_i=(x-x_i, y-y_i),\bm{e}_i=\dfrac{\bm{v}_i}{|\bm{v}_i|}$とすると、条件は$\bm{e}_1+\bm{e}_2+\bm{e}_3=\bm{0}$で$|\bm{e}_1|=|\bm{e}_2+\bm{e}_3|$から両辺2乗して$\bm{e}_2\cdot\bm{e}_3=-\dfrac12$。同様にして$\bm{e}_1\cdot\bm{e}_2=\bm{e}_3\cdot\bm{e}_1=-\dfrac12$から$\bm{e}_1,\bm{e}_2,\bm{e}_3$のうち任意の2つがなす角は$\dfrac{2}3\pi$。
また、$A$を中心とする半径$f(A)$の円の内部と周を$D$とすると、$P\in\RR\setminus D$に対し$f(P)>PA>f(A)$だから$P\in\RR^2$における$f(P)$の最小値は$P\in D$におけるものと一致するが、定理13より$P\in D$における最小値は存在するから、$f(x,y)$は$\RR^2$で最小値を持つ。

1. $\max\q{\angle A,\angle B,\angle C}<\dfrac23\pi$のとき
   まず、$\triangle ABC$の内部の点$F$があって$\angle AFB=\angle BFC=\angle CFA=\dfrac{2}3\pi$を満たすことを示す。辺$AB$の垂直二等分線上を動く点$N$を中心とし、$A,B$を通る円$\Gamma_N$を考え、$F$は$AB$に対して$C$と同じ側の弧$\stackrel{\huge\frown}{AB}$上にあるとする。
   
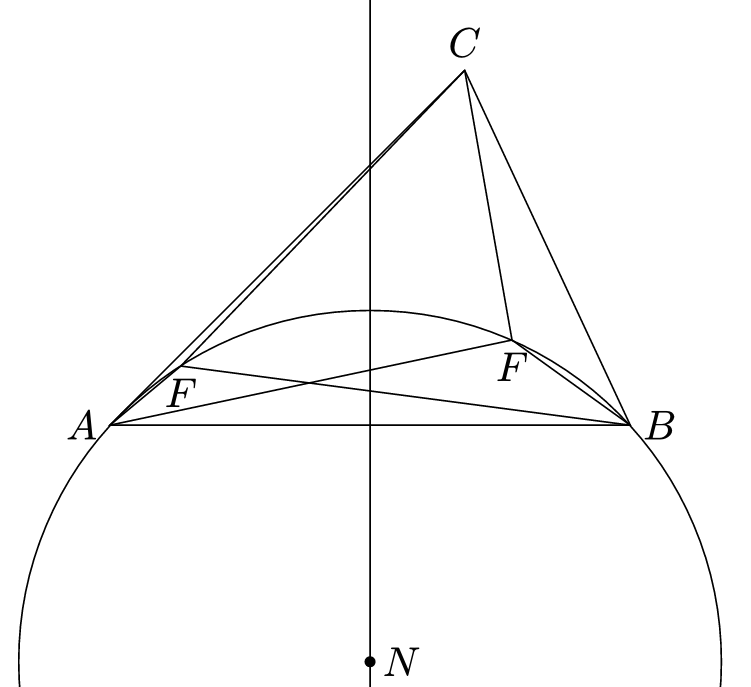
   このとき、円周角の定理より$\angle AFB$は$N$の位置のみに依存し、$N$が図において下に無限に行けば$\angle AFB\to\pi$で、$\Gamma_N$が円$ABC$と一致するとき$\angle AFB=\angle ACB<\dfrac23\pi$であるから、中間値の定理よりある$N$があって、$\angle AFB=\dfrac23\pi$を満たす。また、この$N$に対して、同じように弧$\stackrel{\huge\frown}{AB}$上に$F$をとると、$F=A$のとき$\angle AFC=\pi$であり、$F=B$のとき$\angle AFC=\angle ABC<\dfrac23\pi$であるから、中間値の定理より$\angle AFC=\dfrac23\pi$を満たす$F$が存在する。よって、示された。
   よって、この$F$は(1)の条件を満たすが、このような$F$の一意性は明らかであるから、$f(x,y)$が最小値を持つことより、最小値を取る点の候補は$F,A,B,C$。いま余弦定理より$AB^2=FA^2+FB^2+FA\cdot FB, AC^2=FA^2+FC^2+FA\cdot FC$だから、$a=FA,b=FB,c=FC$とすると
   \begin{align} f(A)^2-f(F)^2&=(AB+AC)^2-(FA+FB+FC)^2\\ &=2AB\cdot AC+a^2+b^2+ab+a^2+c^2+ca-a^2-b^2-c^2-2ab-2bc-2ca\\ &=2\sqrt{(a^2+b^2+ab)(a^2+c^2+ca)}+a^2-ab-2bc-ca\\ \end{align}
   ここで
   \begin{align} &4(a^2+b^2+ab)(a^2+c^2+ca)-(-a^2+ab+2bc+ca)^2\\ &=4(a^4+(b+c)a^3+(b^2+bc+c^2)a^2+abc(b+c)+b^2c^2)-(a^4+2(b+c)a^3+(b^2-2bc+c^2)a^2+4abc(b+c)+4bc^2)\\ &=a^2(3a^2+2(b+c)a+(b+c)^2)\\ &=a^2\q(3\q(a+\frac{b+c}3)^2+\frac23\q(b+c)^2)\\ &>0 \end{align}
   から$4(a^2+b^2+ab)(a^2+c^2+ca)-(-a^2+ab+2bc+ca)^2>0$より$2\sqrt{(a^2+b^2+ab)(a^2+c^2+ca)}+a^2-ab-2bc-ca>0$だから($x^2>y^2$のとき、$x>0$であれば$y$の符号に関わらず$x>y$)$f(A)^2-f(F)^2>0$、$f(A),f(F)>0$だから$f(A)>f(F)$。同様にして$f(B),f(C)>f(F)$だから$f(F)$が最小値。よって、求める点は$F$。
2. $\max\q{\angle A,\angle B,\angle C}\geq\dfrac23\pi$のとき
   このとき、(1)を満たす$P$が存在したとするとある点$F$があって$\angle AFB=\angle BFC=\angle CFA=\dfrac23\pi$を満たすが、そのような$F$が内部または周上にあることは$\max\q{\angle A,\angle B,\angle C}\geq\dfrac23\pi$よりありえず、外部にあるとすると図のようになり$\dfrac23\pi+\dfrac23\pi=\dfrac23\pi$から不適。よって(1)をみたす$P$は存在しない。
   
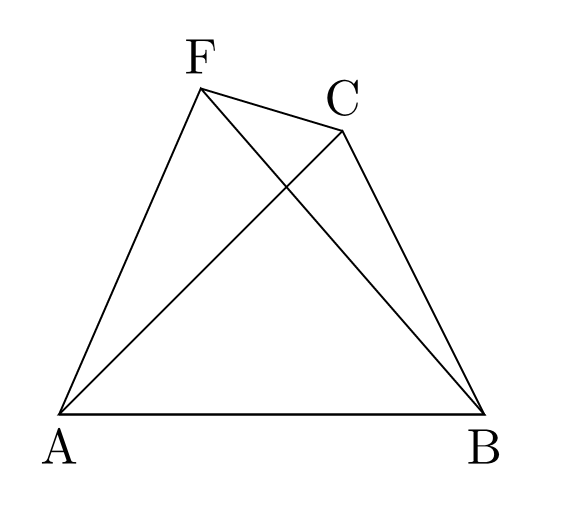
   よって$f$は極値を持たないが、最小値を持つからその候補は$A,B,C$。$\max\q{\angle A,\angle B,\angle C}=\angle A>\dfrac23\pi$として一般性を失わない。このとき、
   \begin{align} BC^2=AB^2+AC^2-2AB\cdot AC\cos\angle A \end{align}
   より
   \begin{align} AB+AC-(AB+BC)&=AC-BC\\ &=AC-\sqrt{AB^2+AC^2-2AB\cdot AC\cos\angle A}\\ &=\dfrac{AB(2AC\cos\angle A-AB)}{AC+\sqrt{AB^2+AC^2-2AB\cdot AC\angle A}}\\ &<0\quad (\because \cos\angle A<-\frac12<0)\\ AB+AC-(AC+BC)&=AB-BC\\ &=AB-\sqrt{AB^2+AC^2-2AB\cdot AC\cos\angle A}\\ &=\dfrac{AC(2AB\cos\angle A-AC)}{AB+\sqrt{AB^2+AC^2-2AB\cdot AC\angle A}}\\ &<0\quad (\because \cos\angle A<-\frac12<0)\\ \end{align}
   から、$f(A)$が最小、よって求める点は$A$。

1. \begin{align} \int x^n e^{ax}e^{ibx}dx &=\int x^ne^{ax}\cos bxdx+i\int x^ne^{ax}\sin bxdx\\ &=\frac{x^n e^{(a+ib)x}}{a+ib}-\frac{1}{a+ib}\int x^{n-1}e^{(a+ib)x}dx \end{align}
   で$\ds\int e^{(a+ib)x}dx=\frac{e^{a+ib}x}{a+ib}$より帰納的に示される。
2. $\ds\int\prod_{k=1}^p \cos^{e_k} a_kx \prod_{l=1}^q\sin^{e'_l} b_lx dx$が積分できることを示せば十分。いま
   \begin{align} \cos \alpha\cos \beta&=\dfrac{\cos(\alpha+\beta)+\cos(\alpha-\beta)}2\\ \cos\alpha\sin\beta&=\dfrac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}\\ \sin\alpha\sin\beta&=\dfrac{\cos(\alpha-\beta)-\cos(\alpha+\beta)}{2} \end{align}
   より、結局$\ds\int\cos\lambda x dx$または$\ds\int\sin\mu x dx$の形になるから、これは積分できる。
3. (2)と同様にして、結局$\ds\int e^{cx}Q(x)\cos xdx,\ \int e^{cx}Q(x)\sin x dx$の形になり、これは(1)より積分できる。
4. \begin{align} \int R'(x)\log xdx&=R(x)\log x-\int \frac{R(x)}x dx\\ \int R'(x)\arctan xdx&=R(x)\arctan x-\int \frac{R(x)}{1+x^2}dx\\ \int R'(x)\arcsin xdx&=R(x)\arcsin x-\int \frac{R(x)}{\sqrt{1-x^2}}dx\\ &=R(x)\arcsin x -\int R(\sin u)du \quad (x=\sin u) \end{align}
   より、(2)からこれは積分できる。

$\cos x = \q(\dfrac{e^{ix}+e^{-ix}}2)$より、
\begin{align} \int \cos^n x dx&=\int \q(\dfrac{e^{ix}+e^{-ix}}2)^n dx\\ &=2^{-n}\int\sum_{k=0}^n \binom{n}{k} e^{ikx}e^{-(n-k)ix}dx\\ &=2^{-n}\sum_{k=0}^n \binom{n}{k} \int e^{(2k-n)ix}dx \end{align}
$n$が偶数のとき、
\begin{align} \phantom{\int \cos^n x dx}&=2^{-n}\q(\sum_{k=0}^{\frac n2-1}\binom{n}{k} \frac{e^{(2k-n)ix}}{(2k-n)i}+\binom{n}{\frac n2}x+\sum_{k=\frac n2+1}^n \binom{n}k \frac{e^{(2k-n)ix}}{(2k-n)i})\\ &=2^{-n}\q(\sum_{k=0}^{\frac n2-1}\binom{n}{k} \frac{e^{(2k-n)ix}}{(2k-n)i}+\binom{n}{\frac n2}x+\sum_{k=0}^{\frac{n}2-1} \binom{n}{n-k} \frac{e^{(n-2k)ix}}{(n-2k)i})\\ &=2^{-n}\q(\sum_{k=0}^{\frac n2-1}\binom{n}{k}\frac{e^{(2k-n)ix}-e^{-(2k-n)ix}}{(2k-n)i}+\binom{n}{\frac n2}x)\\ &=2^{-n}\q(\sum_{k=0}^{\frac n2-1}\binom{n}{k}\frac{2\sin(2k-n)x}{(2k-n)}+\binom{n}{\frac n2}x) \end{align}
$n$が奇数のとき、
\begin{align} \phantom{\int \cos^n x dx}&=2^{-n}\q(\sum_{k=0}^n \binom{n}{k} \frac{e^{(2k-n)ix}}{(2k-n)i})\\ &=2^{-n}\q(\sum_{k=0}^{\frac{n-1}2} \binom{n}{k} \frac{e^{(2k-n)ix}}{(2k-n)i}+\sum_{k=\frac{n+1}2}^n \binom{n}{k} \frac{e^{(2k-n)ix}}{(2k-n)i})\\ &=2^{-(n+1)}\sum_{k=0}^{\frac {n-1}2}\binom{n}{k}\frac{\sin(2k-n)x}{(2k-n)} \end{align}

\begin{align} \int \sin^{\alpha-1}x\cos(\alpha+1)xdx&=\int \q(\sin^{\alpha-1}x\cos\alpha x\cos x-\sin^{\alpha-1}x\sin\alpha x\sin x)dx\\ &=\int \frac1\alpha (\sin^{\alpha x})'\cos \alpha x dx-\int\sin^{\alpha}x\sin\alpha xdx\\ &=\frac1\alpha\sin^{\alpha x}\cos \alpha x \end{align}
となる。他も同様。

多項式$P$を$P(x,y)=\ds\sum_{i=0}^nx^i\q(\sum_{j=0}^m a_{ij}y^{2j}+\sum_{j=0}^mb_{ij}y^{2j+1})$とすると
\begin{align} P(\cos\theta,\sin\theta)&=\sum_{i=0}^n\cos^i\theta\q(\sum_{j=0}^m a_{ij}\sin^{2j}\theta+\sum_{j=0}^mb_{ij}\sin^{2j+1}\theta)\\ &=\sum_{i=0}^n\cos^i\theta\sum_{j=0}^m a_{ij}(1-\cos^2\theta)^j+\q(\sum_{i=0}^n\cos^i\theta\sum_{j=0}^m b_{ij}\q(1-\cos^2\theta)^j)\sin\theta \end{align}
より$P(\cos\theta,\sin\theta)=\alpha_P(\cos\theta)+\beta_P(\cos\theta)\sin\theta$と表される。よって、
\begin{align} F(\cos x,\sin x)&=\frac{P(\cos x,\sin x)}{Q(\cos x,\sin x)}\\ &=\frac{\alpha_P+\beta_P\sin x}{\alpha_Q+\beta_Q\sin x}\\ &=\frac{(\alpha_P+\beta_P\sin x)(\alpha_Q-\beta_Q\sin x)}{\alpha_Q^2-\beta_Q^2(1-\cos^2 x)}\\ &=\frac{\alpha_P\alpha_Q-\beta_P\beta_Q(1-\cos^2x)+(\alpha_Q\beta_P-\alpha_P\beta_Q)\sin x}{\alpha_Q^2-\beta_Q^2(1-\cos^2 x)} \end{align}
から示される。また、多項式$P$が$P(\cos\theta)=\alpha_P(\cos^2\theta)+\beta_P(\cos^2\theta)\cos\theta$と分解できるのは明らか。
\begin{align} f(\cos x)&=\dfrac{R(\cos x)}{S(\cos x)}\\ &=\dfrac{\alpha_R+\beta_R\cos x}{\alpha_S+\beta_S\cos x}\\ &=\dfrac{\alpha_R\alpha_S-\beta_R\beta_S\cos^2x+(\alpha_S\beta_R-\alpha_R\beta_S)\cos x}{\alpha_S^2-\beta_S^2\cos^2x} \end{align}
から示される。

1. \begin{align} (p+q+1)I_{p,q}-qbI_{p,q-1}&=(p+q+1)\int t^p(at+b)^qdt-qb\int t^p(at+b)^{q-1}dt\\ &=\int t^p(at+b)^{q-1}((p+q+1)(at+b)-qb)dt\\ &=\int t^p(at+b)^{q-1}((p+1)(at+b)-atq)dt\\ &=\int \q(\q(p+1)t^p\q(at+b)^q-atqt^p\q(at+b)^{q-1})dt\\ &=t^{p+1}(at+b)^q \end{align}
2. (1)と同様。

1. $a=0$のとき明らか。$a\ne0$のとき、
   \begin{align} \int_0^\pi \frac{\sin x}{\sqrt{1-2a\cos x+a^2}}dx &=\int_{-1}^1 \frac{dt}{\sqrt{-2at+a^2+1}}\quad (t=\cos x)\\ &=\left.-\frac{\sqrt{-2at+1+a^2}}{a}\right|_{-1}^1\\ &=-\frac{|a-1|-|a+1|}{a}\\\\ &=\left\{ \begin{array}{l} 2,\quad&|a|\leq1\\ \dfrac{2}{|a|},&|a|\geq1 \end{array} \right. \end{align}
2. \begin{align} \int_0^1 \frac{x\log x}{(1+x)^4}dx&=\int_1^2 \frac{(t-1)\log(t-1)}{t^4}dt\\ &=\int_1^2 \q(\frac{\log\q(t-1)}{t^3}-\frac{\log\q(t-1)}{t^4}) \end{align}
   であり、
   \begin{align} \int \frac{\log(t-1)}{t^3} &=-\frac{\log(t-1)}{2t^2}+\int\frac{dt}{2t^2(t-1)}\\ &=-\frac{\log(t-1)}{2t^2}+\frac12\int\q(\frac{-t-1}{t^2}+\frac1{t-1})\\ &=-\frac{\log(t-1)}{2t^2}+\frac12\q(-\log t+\frac1t+\log(t-1))\\ &=\frac{1}{2}\q(-\frac{(t+1)(t-1)\log(t-1)}{t^2}-\log t+\frac1t)\\ \int \frac{\log(t-1)}{t^4} &=-\frac{\log(t-1)}{3t^3}+\int\frac{dt}{3t^3(t-1)}\\ &=-\frac{\log(t-1)}{3t^3}+\frac13\int\q(-\frac{t^2+t+1}{t^3}+\frac{1}{t-1})\\ &=-\frac{\log(t-1)}{3t^3}+\frac13\q(\log\q(t-1)-\log t+\frac1t+\frac1{2t^2})+\text{Const}\\ &=\frac13\q(-\frac{(t^2+t+1)(t-1)\log(t-1)}{t^3}-\log t+\frac1t+\frac1{2t^2}) \end{align}
   から、$[1,2]$で積分して
   \begin{align} \int_1^2 \frac{\log(t-1)}{t^3}&=\frac12\q(-\log2-\frac12)\\ \int_1^2 \frac{\log(t-1)}{t^4}&=\frac13\q(-\log2-\frac78) \end{align}
   より示される。

1. \begin{align} \int_a^b \frac{dx}{\sqrt{(x-a)(b-x)}} &=\int_0^1\frac{dt}{\sqrt{t(1-t)}}\quad (x=ta+(1-t)b)\\ &=\int_0^1\frac{2du}{\sqrt{1-u^2}}\quad(t=u^2)\\ &=2\arcsin u\bigg|_0^1\\ &=\pi \end{align}
2. \begin{align} \int_{-1}^1 \frac{dx}{(a-x)\sqrt{1-x^2}} &=\int_{0}^\pi \frac{dt}{a-\cos t}\quad (x=\cos t)\\ &=2\int_0^\infty \frac{dt}{(a+1)t^2+a-1}\quad \q(u=\tan \frac t2)\\ &=\frac{2}{a-1}\sqrt{\frac{a-1}{a+1}}\eval{\arctan\sqrt{\frac{a+1}{a-1}}t}_0^\infty\\ &=\frac{\pi}{a-1}\sqrt{\frac{a-1}{a+1}}\\ &=\frac{\pm\pi}{\sqrt{(a-1)^2}}\sqrt{\frac{a-1}{a+1}}\\ &=\frac{\pm\pi}{\sqrt{a^2-1}} \end{align}
   ただし$\pm$は$a$の符号。
3. $\S34$[例3]より、
   \begin{align} \int_0^{\frac\pi2} \q(\frac\pi2-x)\tan xdx &=\int_0^{\frac\pi2} \frac{u}{\tan u}\quad\q(u=\frac\pi2-x)\\ &=u\log\sin u\bigg|_0^{\frac\pi2}-\int_0^{\frac\pi2} \log \sin u du\\ &=\frac{\pi}2\log 2 \end{align}
4. \begin{align} \int_0^1\frac{\log x}{x^\alpha}dx &=\eval{\frac{\log x}{(1-\alpha)x^{\alpha-1}}-\frac{1}{(1-\alpha)^2x^{\alpha-1}}}_0^1\\ &=\frac{-1}{(1-\alpha)^2}\quad (\because 0<\alpha<1) \end{align}

$1<\nu<2$のとき、
\begin{align} \int_0^\infty \abs{\frac{\sin x}{x^\nu}}dx &\leq\int_0^1\frac{\sin x}{x^\nu}dx+ \int_1^\infty \frac{dx}{x^\nu}\\ &\leq\int_0^1 \frac{dx}{x^{\nu-1}}+\int_1^\infty \frac{dx}{x^\nu}\quad(\because \sin x\leq x)\\ &<\infty \end{align}
より絶対収束。
$0<\nu\leq1$のとき、$0< s< t$に対して
\begin{align} \abs{\int_s^t \frac{\sin x}{x^\nu}dx} &=\abs{-\eval{\frac{\cos x}{x^\nu}}_s^t-\int_s^t\frac{\nu\cos x}{x^{\nu+1}}}\\ &=\abs{\frac{\cos t}{t^\nu}-\frac{\cos s}{s^\nu}+\int_s^t\frac{\nu\cos x}{x^{\nu+1}}}\\ &\leq\abs{\frac{\cos t}{t^\nu}}+\abs{\frac{\cos s}{s^\nu}}+\abs{\int_s^t\frac{\nu\cos x}{x^{\nu+1}}}\\ &\leq\frac{1}{t^\nu}+\frac{1}{s^\nu}+\int_s^t \frac{1}{x^{\nu+1}}dx\\ &\leq \frac{2}{s^\nu}-\eval{\frac{1}{\nu x^\nu}}_s^t\\ &=\frac{2}{s^\nu}-\frac{1}{\nu t^\nu}+\frac{1}{\nu s^\nu}\\ &\leq \q(2+\frac1\nu)s^{-\nu}\\ &\to 0\quad (s\to \infty) \end{align}
よりCauthyの収束条件からこれは収束する。
$\ds\int_0^\infty \abs{\frac{\sin x}{x^{\nu}}}dx$が収束しないことを示す。
\begin{align} \int_{n\pi}^{(n+1)\pi} \abs{\frac{\sin x}{x^{\nu}}}dx &=\int_0^\pi\abs{\frac{\sin x}{(n\pi+u)^\nu}} \quad (u=x-n\pi)\\ &>\frac{2}{(n+1)^\nu\pi^\nu} \end{align}
だから、
\begin{align} \int_0^\infty \abs{\frac{\sin x}{x^{\nu}}}dx &=\sum_{n\geq0}\int_{n\pi}^{(n+1)\pi} \abs{\frac{\sin x}{x^{\nu}}}dx\\ &>\sum_{n\geq0}\frac{2}{(n+1)^\nu\pi^\nu}\\ &=\frac{2}{\pi^\nu}\sum_{n\geq1}\frac{1}{n^\nu}\\ &=\infty \end{align}
からこれは収束しない。よって、$0<\nu\leq1$で条件収束。

\begin{align} \int_{n\pi}^{(n+1)\pi} \abs{\frac{x}{1+x^6\sin^2 x}}dx &\leq(n+1)\pi\int_{n\pi}^{(n+1)\pi} \frac{dx}{1+(n\pi)^6\sin^2 x}\\ &=(n+1)\pi\int_0^\pi \frac{du}{1+(n\pi)^6\sin^2 u}\quad (u=x-n\pi)\\ &=2(n+1)\pi\int0^{\frac\pi2}\frac{du}{1+(n\pi)^6\sin^2 u}\\ &=2(n+1)\pi\int_0^\infty \frac{dt}{((n\pi)^6+1)t^2+1} \quad(t=\tan u)\\ &=2(n+1)\pi\eval{\frac{1}{\sqrt{(n\pi)^6+1}}\arctan \sqrt{(n\pi)^6+1}t}_0^\infty\\ &=\frac{(n+1)\pi^2}{\sqrt{(n\pi)^6+1}}\\ \end{align}
いま
\begin{align} \frac{1}{n^4}-\q(\frac{(n+1)\pi^2}{\sqrt{(n\pi)^6+1}})^2 &=\frac{(n\pi)^6+1-n^4(n+1)^2\pi^4}{n^4((n\pi)^6+1)}\\ &=\frac{n^4\pi^4((\pi-1)n-1)((\pi+1)n+1)+1}{n^4((n\pi)^6+1)}\\ &>0 \end{align}
から$\ds\frac{(n+1)\pi^2}{\sqrt{(n\pi)^6+1}}<\frac{1}{n^2}$
より
\begin{align} \int_0^\infty \abs{\frac{x}{1+x^6\sin^2 x}}dx<\int_0^\pi\abs{\frac{x}{1+x^6\sin^2 x}}dx+\sum_{n>0}\frac{1}{n^2}<\infty \end{align}

\begin{align} J_n&=\int_0^1 \frac{x^n}{\sqrt{1-x^4}}dx\\ &=\int_0^{\frac\pi2}\frac{\sin^{\frac n2}u}{\cos u}\cdot\frac{\cos u}{2\sqrt{\sin u}}\quad(x=\sqrt{\sin u})\\ &=\frac12\int_0^{\frac\pi2} \sin^{\frac{n-1}2}udu\\ &=\frac12\int_0^{\frac\pi2} -\sin^{\frac{n-3}2}u(\cos u)'du\\ &=\frac12\q(-\sin^{\frac{n-3}2}u\cos u\bigg|_0^\frac{\pi}2+\frac{n-3}2\int_0^{\frac\pi2}\sin^{\frac{n-5}2}u\q(1-\sin^2 u)du)\\ &=\frac{n-3}2\q(\frac12\int_0^{\frac\pi2} \sin^{\frac{n-5}2}udu-\frac12\int_0^{\frac\pi2} \sin^{\frac{n-1}2}udu)\\ &=\frac{n-3}2\q(J_{n-4}-J_n) \end{align}

$g(x)$が定数関数$g(x)=0$ならば明らか。そうでないとき、$f,g$が可積分だから$\lambda\in\RR$に対して$(f(x)+\lambda g(x))^2$も可積分。よって、
\begin{align} \int_a^b (f(x)+\lambda g(x))^2dx=\int_a^b f(x)^2dx+2\lambda\int_a^b f(x)g(x)dx+\lambda^2\int_a^b g(x)^2dx\geq0 \end{align}
から、これを$\lambda$の2次式と見て
\begin{align} \q(\int_a^b f\q(x)g\q(x)dx)^2-\q(\int_a^b f\q(x)^2dx)\q(\int_a^b g\q(x)^2dx)\leq0 \end{align}
から示される。等号は、$f=0$または$g=0$または$\lambda$の2次式が重解$\xi$を持つときで、$f,g$が連続ならばこれは$f+\xi g=0$と同値。これはつまり$f,g$の比が定数であることである。

$A=(a_{ij})$とし、$A$の二次形式を$q_A(\bm{x})$とすると、
\begin{align} \int_a^b \q(\sum_{i=1}^n u_if_i\q(x))^2dx &=\sum_{i=1}^n\sum_{j=1}^n u_iu_j \int_a^b f_i(x)f_j(x)dx\\ &=q_A(\bm{x})\\ &\geq0 \end{align}
より、$A$の2次形式が非負だから$|A|\geq0$。また、$f_1,\cdots,f_n$が連続ならば$\ds\sum_{i=1}^n u_if_i\ne0$のとき$q_A(\bm{x})>0$だから$|A|>0$。よって、$|A|=0$ならばある$\bm{x'}\ne\bm{0}$があって$q_A(\bm(x'))=0$を満たすから$\bm{u}(x)=(f_1(x),\cdots,f_n(x))$とすると$\bm{x'}\cdot\bm{u}=0,\bm{x'}\ne0$を満たし、示される。

$m\leq n$として一般性を失わない。$H_n'(x)=2nH_{n-1}(x)$を示す。帰納法による。$H_0(x)=1,H_1(x)=2x$より$n=1$では明らか。$H_n'(x)=2nH_{n-1}(x)$を仮定すると、
\begin{align} H_n'(x)&=(-1)^n2xe^{x^2}\dvn{x}{n}e^{-x^2}-(-1)^{n+1}e^{x^2}\dvn{x}{n+1}e^{-x^2}\\ &=2xH_n(x)-H_{n+1}(x) \end{align}
の両辺微分して
\begin{align} H_{n+1}'(x)&=2H_n(x)+2xH_n'(x)-H_n''(x)\\ &=2H_n(x)+2x2nH_{n-1}(x)-2nH_{n-1}'(x)\\ &=2H_n(x)+2n(2xH_{n-1}(x)-H_{n-1}'(x))\\ &=2(n+1)H_n(x) \end{align}
から示される。$x^{k}\dvn{x}{n}e^{-x^2}\to0\ \ (n\to\pm\infty)$を示す。練習問題(2)-(3)より、$H_n(x)$は$n$次の多項式だから
\begin{align} \q|x^{k}\dvn{x}{n}e^{-x^2}| &=\q|x^kH_n(x)(-1)^ne^{-x^2}|\\ &\leq\q|nx^{n+k}e^{-x^2}|\\ &\to0 \end{align}
から示される。以上より、
\begin{align} \int_{-\infty}^{\infty}H_m(x)H_n(x)e^{-x^2} &=\int_{-\infty}^{\infty}H_m(x)(-1)^ne^{x^2}\q(\dvn{x}{n}e^{-x^2})e^{-x^2}dx\\ &=(-1)^n\int_{-\infty}^{\infty} H_m(x)\dvn{x}{n}e^{-x^2}dx\\ &=(-1)^n\left(H_m(x)\dvn{x}{n-1}e^{-x^2}\bigg|_{-\infty}^\infty-\int_{-\infty}^\infty H_m'(x)\dvn{x}{n-1}e^{-x^2}dx\right)\\ &=(-1)^{n+1}2m\int_{-\infty}^\infty H_{m-1}(x)\dvn{x}{n-1}e^{-x^2}dx\\ &=(-1)^{n+m}2^mm!\int_{-\infty}^\infty \dvn{x}{n-m}e^{-x^2}dx\\ &=\left\{\begin{array}{l} 2^nn!\ds\int_{-\infty}^\infty e^{-x^2}dx\quad&(n=m)\\ \ds(-1)^{n+m}2^mm!\int_{-\infty}^\infty \dvn{x}{n-m}e^{-x^2}dx&(n\ne m) \end{array}\right.\\ &=\delta_{mn}2^nn!\sqrt{\pi} \end{align}

$D=\dv x$とする。$n\leq m$として一般性を失わない。$a,b,p\in \mathbb{Z}_{>0}, b\geq p$のとき
\begin{align} x^a D^p x^be^{-x}dx\bigg|_0^\infty=0 \end{align}
を示す。
\begin{align} x^a D^p x^be^{-x}dx &=x^a\sum_{k=0}^p \binom{p}{k}\q(D^{k}x^b)\q(D^{p-k}e^{-x})\\ &=x^a\sum_{k=0}^p \binom{p}{k}\frac{b!}{(b-k)!}x^{b-k}(-1)^{p-k}e^{-x} \end{align}
より、$x\to\infty,0$で各項$0$に飛ぶから示される。また、$q>0,c\geq p,d\geq q$として
\begin{align} e^x(D^px^ce^{-x})(D^qx^de^{-x})\bigg|_0^\infty=0 \end{align}
も同様に示される。よって、
\begin{align} \int_0^\infty L_m(x)L_n(x)e^{-x}dx &=\int_0^\infty L_m(x)e^x\q(D^n x^ne^{-x})e^{-x}dx\\ &=\int_0^\infty L_m(x)D^n x^ne^{-x}dx\\ &=\int_0^\infty e^x(D^mx^me^{-x})(D^n x^ne^{-x})dx\\ &=e^x(D^mx^me^{-x})(D^{n-1}x^ne^{-x})\bigg|_0^\infty -\int_0^\infty D(e^x(D^mx^me^{-x}))(D^{n-1}x^ne^{-x})dx\\ &=-\int_0^\infty D(e^xD^mx^me^{-x})(D^{n-1}x^ne^{-x})dx\\ &=(-1)^n\int_0^\infty D^n(e^xD^mx^me^{-x})x^ne^{-x}dx\\ &=(-1)^n\int_0^\infty \sum_{k=0}^n \binom{n}{k}e^x(D^{m+k}x^me^{-x})x^ne^{-x}dx\\ &=(-1)^n\sum_{k=0}^n \binom{n}{k}\int_0^\infty x^nD^{m+k}x^me^{-x}dx\\ &=(-1)^n\sum_{k=0}^n \binom{n}{k}\q(x^nD^{m+k-1}x^me^{-x}\bigg|_0^\infty-\int_0^\infty nx^{n-1}D^{m+k-1}x^me^{-x}dx)\\ &=(-1)^n\sum_{k=0}^n \binom{n}{k}(-1)^nn!\int_0^\infty D^{m+k-n}x^me^{-x}dx\\ &=n!\sum_{k=0}^n \binom{n}{k}\int_0^\infty D^{m+k-n}x^me^{-x}dx \end{align}
ここで、Gamma関数の定義より
\begin{align} \int_0^\infty D^{m+k-n}x^me^{-x}dx &=\left\{\begin{array}{l} m!\quad&(m+k-n=0)\\ 0\quad&(m+k-n>0) \end{array}\right. \end{align}
であり、$n=m+k\iff n\geq m$、いま$n\leq m$としているから$n=m,k=0$。よって、
\begin{align} \int_0^\infty L_m(x)L_n(x)e^{-x}dx &=n!\sum_{k=0}^n \binom{n}{k}\delta_{nm}\delta_{k0}m!\\ &=\delta_{nm}n!m!\\ &=\delta_{nm}(n!)^2 \end{align}

\begin{align} \int_0^1 f(x) &=\lim_{n\to\infty}\frac{1}{2^n}\sum_{k=0}^{2^n}f\q(\frac{k}{2^n}) \end{align}
より
\begin{align} 2^{-n}\sum_{k=0}^{2^n}f\q(\frac{k}{2^n}) &=2^{-n}\q(f\q(\frac{1}{2^n})+f\q(\frac{2}{2^n})+\cdots+f\q(\frac{2^n}{2^n}))\\ &=20^{-n}\q(1+10+11+\cdots+10^n)\\ &=20^{-n}\q(\sum_{k=0}^{n-1}2^{n-1}10^k+10^n)\\ &=20^{-n}\q(\dfrac{2^{n-1}(10^n-1)}{9}+10^n)\\ &=\dfrac{1-10^{-n}}{18}+2^{-n}\\ &\to\dfrac1{18} \end{align}
から示される。