スピン群入門の入門

サークルのアドカレ企画 で記事を書くことになったので，スピン群の紹介記事を書きます．
自分はスピン幾何を専門として勉強してる修士1年です．スピン幾何を勉強する仲間が増えたら嬉しいです．

スピン群とは特殊直交群$\SO(n)$の二重被覆群のことです．(詳細は後述)
この記事ではスピン群を具体的に構成し，簡単に性質などを説明することを目標とします．
スピン群を定義するために，まずクリフォード代数について説明します．

記法

$e_1, \cdots, e_n \in \R^n$を標準基底とします．$\R^n$の通常の内積を$\langle v, w\rangle$のようにカッコで表します．$n\times n$の正則な実行列全体がなす群を一般線形群と呼び$\GL(\R^n)$と表します．また
$$ \O(n) = \{A \in \GL(\R^n) \mid {}^tAA = I\}$$
を直交群と言います．直交群の要素は行列式が$\pm 1$になっていますが，そのうち行列式が1のものだけからなる群を特殊直交群と言い$\SO(n)$と表します．
$$\SO(n) = \{A \in \GL(\R^n) \mid {}^tAA = I, \det(A) = 1\}$$

クリフォード代数

定義

まずクリフォード代数の定義を雑に説明します．代数の知識がある人のためにちゃんとした(厳密な)定義を後で与えます．
ベクトル$v,w \in \R^n$に対して，それらの積$vw$を考えます．この積は内積や外積ではなく，2つのベクトルを形式的に並べているだけです．ただし次のような計算規則を与えます．
$$ vw + wv = -2\langle v, w\rangle$$
この計算規則の意味を理解するために，$v=e_i, w=e_j$の場合を考えてみると
$i \neq j$のとき$e_ie_j + e_je_i = 0$，すなわち$e_ie_j = -e_je_i$となります．一方で$i=j$のとき$e_ie_i + e_ie_i = -2$，すなわち$e_ie_i = -1$となります．

このような積を考えることで作られる要素全部を集めた集合をクリフォード代数といい$\Cl_n$と表します．クリフォード代数は和とスカラー倍が定義されていてベクトル空間になります．例えば次は$\Cl_3$の基底になります．
$$ 1,\, e_1,\, e_2,\, e_3,\, e_1e_2,\, e_1e_3,\, e_2e_3,\, e_1e_2e_3$$
したがって$\Cl_3$はベクトル空間としては8次元です．一般の$n$でも同じように基底が作れて，$\Cl_n$は$2^n$次元のベクトル空間になります．またこれからわかる通り自然に$\R^n \subset \Cl_n$とみなせます．

鏡映

クリフォード代数には色々な面白い性質があるのですが，その中でも今回の内容に関連する性質を1つ紹介しておきます．
$v,a \in \R^n\,\, (a \neq 0)$とし，$a$に直交する超平面($(n-1)$次元部分空間)に関する$v$の鏡映を$\Ref_a(v) \in \R^n$と表します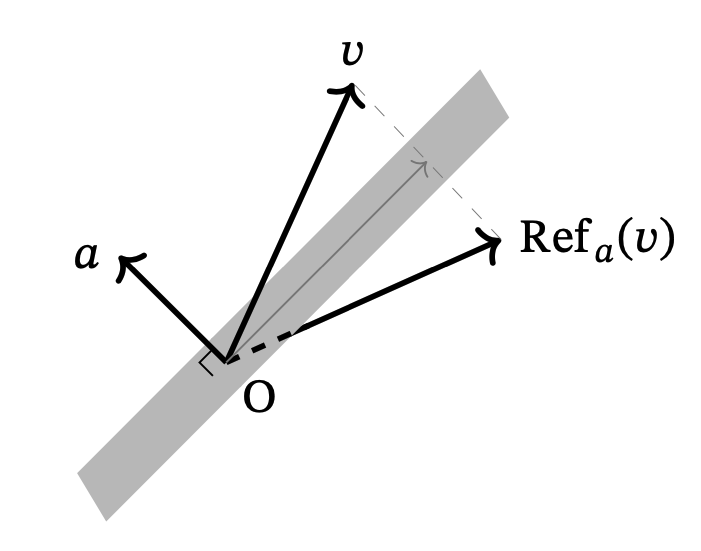． 鏡映
線形代数でよく知られていることですが
$$ \Ref_a(v) = v - 2\frac{\langle v, a\rangle}{\|a\|^2}a$$
と表すことができます(知らない人は図を見ながら考えてみてください)．実はこれはクリフォード代数を用いるともっと簡潔に表すことができます．

スピン群

定義

まずスピン群$\Spin(n)$の定義を与えます．

定義だけ見てもよくわからないかもしれないですが，実はこれは$\SO(n)$の二重被覆になっています．すなわち(局所微分同相な)2:1の全射群準同型$\xi \colon \Spin(n) \to \SO(n)$が存在します．

二重被覆であること

ではどうやってこの二重被覆$\xi$を得るかですが，これに上で述べた鏡映の話が関わってきます．$a \in \R^n \setminus\{0\}$に対して$\Ref_a \colon \R^n \to \R^n$は全単射なので線形同型です．すなわち$\Ref_a \in \GL(\R^n)$です．さらに$\Ref_a$は反射させているだけなので内積を保ちます:
$$\langle \Ref_a(v) ,\Ref_a(w)\rangle = \langle v,w\rangle \quad (\forall v,w \in \R^n)．$$
したがって$\Ref_a \in \O(n)$です．しかしながら鏡映は"向き"を変えてしまうので$\Ref_a \notin \SO(n)$です．(直感的には右手と左手は鏡映の関係にあり，重ねることはできないのと同じです．)結局次がわかります．

ということはベクトルを2つ$a_1,a_2 \in \R^n \setminus \{0\}$用意すれば$$ \det(\Ref_{a_1} \circ \Ref_{a_2}) = (-1)^2 = 1$$
なので$$ \Ref_{a_1} \circ \Ref_{a_2} \in \SO(n)$$となります！
そこで$\xi \colon \Spin(n) \to \SO(n)$を次のように定めます．

スピン群の元はベクトルの偶数個の積で表されていたので，必ず$\xi(a_1a_2 \cdots a_{2m}) \in \SO(n)$となります．

そして$\ker \xi = \{\pm 1\}$なので$\xi$は2:1の写像になっています．つまり$g \in \Spin(n)$に対して$\xi(g) = \xi(-g)$というわけです．また$\xi$が全射であることは次の Cartan–Dieudonnéの定理 から従います．

よく知られている群との同型

とりあえずスピン群の定義はできたわけですが，これだけだとその正体はいまいち掴めません．実は低次のスピン群はよく知られている群と同型になります．

ここで$S^n$は$n$次元球面
$$ S^n = \{(x_1, \cdots, x_{n+1}) \in \R^{n+1} \mid x_1^2 + \cdots + x_{n+1}^2 = 1\},$$
$\U(n), \SU(n)$はそれぞれ$n$次ユニタリ群，$n$次特殊ユニタリ群
\begin{eqnarray} \U(n) &=& \{A \in \GL(\C^n) \mid {}^t\bar{A}A = I\},\\ \SU(n) &=& \{A \in \GL(\C^n) \mid {}^t\bar{A}A = I, \,\,\det(A) = 1\}, \end{eqnarray}
$\Sp(n)$は$n$次シンプレクティック群
$$ \Sp(n) = \{A \in \GL(\H^n) \mid {}^t\bar{A}A = I\},$$
を表します．シンプレクティック群はあまり馴染みがないかもしれませんが，直交群やユニタリ群と同様に$\H^n$上の四元数エルミート内積を保つもの全体のことです．特に$\Sp(1)$は
$$ \Sp(1) = \{a+bi+cj+dk \in \H \mid a^2+b^2+c^2+d^2=1\}$$
です．このことから$S^3 \cong \Sp(1)$であることは明らかです．

よりイメージを掴みやすくするために$n=1,2,3$の場合についてもう少し詳しく説明します．

$\Spin(1)$

$\Spin(1) = \{\pm 1\}$です．$\SO(1) = \{1\}$なので，これはちゃんと二重被覆になっています．
$\Spin(1) \to \SO(1)$

$\Spin(2)$

$\Spin(2) \cong S^1 (\cong \U(1)$)です．$\SO(2) \cong S^1$なので，これだけ見ると二重になってないように思ってしまうかもしれませんがそうではありません．$S^1 = \{z \in \C \mid |z| = 1\}$で表したとき，$\xi$は$z^2$になります．つまり
$$\xi \colon \Spin(2) \cong S^1 \to S^1 \cong \SO(2), \quad \xi(z) = z^2$$
です．図で表すと次のような感じになります． $\Spin(2) \to \SO(2)$

$\Spin(3)$

このへんからは図が描けないので，ある程度知識がある方向けの説明になります．ですが，スピン群のカタチを理解するにはこの例を理解するのが一番わかりやすいと思います．
$\Spin(3) \cong S^3$です．一方で$\SO(3) \cong \R P^3$(実射影空間)ということが知られています．射影空間の定義を思い出すと，$S^3$の中心を挟んだ反対側の点どうしを同一視して得られる空間が$\R P^3$でした． $\R P^3$($S^3$は描けないので$S^2$で$S^3$を表しています．)
なので定義からして$S^3$は$\R P^3$の二重被覆になっているわけです．逆に言えば，$\SO(3) (\cong \R P^3)$の重なっているところを引き剥がしたものが$\Spin(3) (\cong S^3)$であると思うこともできます．

スピン群の性質

まず重要なのは次の性質です．

(i)と(ii)は上の例からわかる通りです．(iii)に関しては$n=3$の場合の具体例から納得できると思います．一般の$n$については少し難しいのですが，$n \geq 3$のとき$\SO(n)$の基本群は$\pi_1(\SO(n)) \cong \Z/2\Z$であるという事実があります．被覆空間の一般論からこれは$\SO(n)$が単連結な二重被覆を持つことを意味します．

スピン群はコンパクトLie群です．また上の具体例からもわかる通り$\Spin(n)$と$\SO(n)$は局所的には同じものとみなせます．したがってそのLie代数は自然に同型になります．
\begin{eqnarray} \xi_{\ast} \colon \mathfrak{spin}(n) \cong \mathfrak{so}(n), \quad \xi_{\ast}(e_ie_j) = 2e_i \wedge e_j\\ (\mathrm{ただし}(e_i \wedge e_j)(x) = \langle e_j, x\rangle e_i - \langle e_i, x\rangle e_j) \end{eqnarray}
ここで$\xi_{\ast}$は$\xi$の微分です．

スピン群の表現

最後におまけで表現について簡単に書いておきます．
Lie群$G$に対して，ベクトル空間$V$とLie群の準同型$\rho \colon G \to \GL(V)$の組$(V, \rho)$をLie群$G$の表現と言います．$\SO(n)$の表現は$\xi$を通すことで自然に$\Spin(n)$の表現になります．すなわち$\rho' \colon \SO(n) \to \GL(V)$が与えられたとき，
$$ \rho := \rho' \circ \xi \colon \Spin(n) \to \GL(V)$$
は$\Spin(n)$の表現です．逆は一般には言えません．$\Spin(n)$の表現$\rho \colon \Spin(n) \to \GL(V)$がもし$\rho(g) = \rho(-g) \, (\forall g \in \Spin(n))$を満たすなら$\rho$は$\SO(n)$上の写像として定義できるので$\SO(n)$の表現になります．
クリフォード代数の既約表現を$\Spin(n)$に制限すると$\Spin(n)$の表現ができるのですが，この表現は上の条件を満たさないため$\SO(n)$の表現になりません．この$\Spin(n)$特有の表現をスピノール表現と言います．