便利さんの積分・級数botを解く⑥
積分を解く
どうも、らららです。
積分・級数botの積分を解きます
今回の積分を解くときに参考にした
動画
解く積分
$$\int_{0}^{\infty}\frac{\sinh x}{x\cosh\frac{x}{a}}dx=\log\cot\frac{\pi(1-a)}{4}$$
積分を解く
留数定理を用いて解いていきます
まず分数をなくすために$x\mapsto ax$と置換します
\begin{align}
I&=\int_{0}^{\infty}\frac{\sinh ax}{ax\cosh x}adx
\\&=\int_{0}^{\infty}\frac{\sinh ax}{x\cosh x}dx
\\&=\int_{0}^{\infty}\frac{e^{ax}-e^{-ax}}{x\left(e^x+e^{-x}\right)}dx
\end{align}
後で理由がわかるんので説明しませんが$f(z)+f(-z)$が被積分関数になれば求めたい積分になるのでそのような$f(z)$を設定します
$\di f(z)=\frac{e^{az}}{z(e^z+e^{-z})}$とすれば
\begin{align}
f(z)+f(-z)&=\frac{e^{az}}{z(e^z+e^{-z})}+\frac{e^{-az}}{-z(e^{-z}+e^z)}
\\&=\frac{e^{az}-e^{-az}}{z(e^z+e^{-z})}
\end{align}
となり$f(z)+f(-z)$が被積分関数になっています
積分経路は半径$R$の半円にします。
そのまま半円だと$z=0$の特異点が経路上にきてしまうので回避します
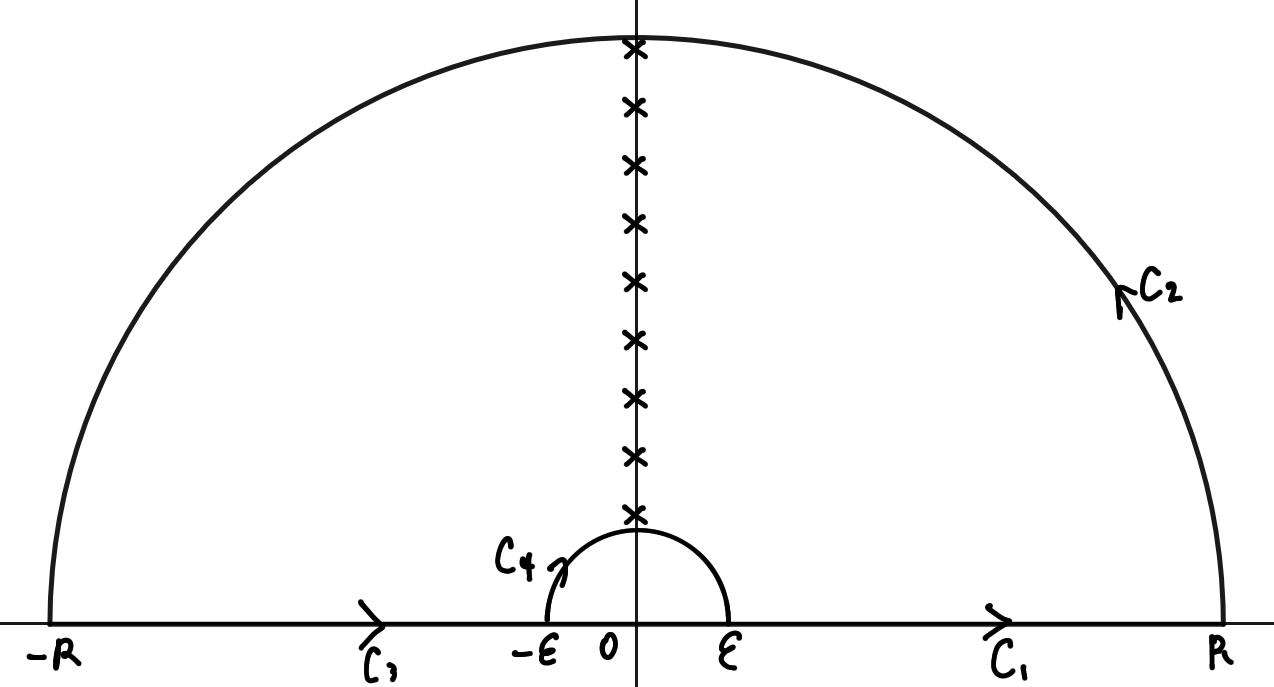 積分経路
積分経路
全体の積分を$C$としておきます
虚軸に×がたくさんあるのは$f(z)$の特異点、つまり$\cosh z=0$となる$z$が$\di i\pi\left(n+\frac12\right)$だからです
それでは計算していきます
\begin{align}
\int_{C_1+C_3}&=\int_{-R}^{-\varepsilon}f(z)dz+\int_{\varepsilon}^{R}f(z)dz
\\&=\int_{\varepsilon}^{R}f(-z)dz+\int_{\varepsilon}^{R}f(z)dz
\\&=\int_{\varepsilon}^{R}\big(f(z)+f(-z)\big)dz
\\&=I\quad(\varepsilon\to0,R\to\infty)
\end{align}
\begin{align}
\lim_{R\to\infty}\int_{C_2}=0
\end{align}
$0$になることの証明は読者への課題とします
\begin{align}
\lim_{\varepsilon\to0}\int_{C_4}&=-i\lim_{\varepsilon\to0}\int_{0}^{\pi}\frac{e^{a\varepsilon e^{i\theta}}}{e^{\varepsilon e^{i\theta}}-e^{-\varepsilon e^{i\theta}}}d\theta
\\&=-i\int_{0}^{\pi}\lim_{\varepsilon\to0}\frac{e^{a\varepsilon e^{i\theta}}}{e^{\varepsilon e^{i\theta}}-e^{-\varepsilon e^{i\theta}}}d\theta
\\&=-i\int_{0}^{\pi}\frac12d\theta
\\&=-\frac{\pi}{2}i
\end{align}
$R\to\infty$とするので特異点は全て入っていると考える
\begin{align}
\oint_{C}&=2\pi i\sum_{n=0}^{\infty}\underset{z=i\pi(n+\frac12)}{\mathrm{Res}}\frac{e^{az}}{z(e^z+e^{-z})}
\\&=2\pi i\sum_{n=0}^{\infty}\lim_{z\to i\pi(n+\frac12)}\frac{e^{az}}{(e^z+e^{-z})+z(e^z-e^{-z})}
\\&=2\pi i\sum_{n=0}^{\infty}\frac{e^{ia\pi(n+\frac12)}}{i\pi(n+\frac12)2(-1)^ni}
\\&=-2i\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}\left(e^{-\frac{ia\pi}{2}}\right)^{2n+1}
\\&=-2i\arctan e^{-\frac{ia\pi}2}
\end{align}
$$I-\frac{\pi}{2}i=-2i\arctan e^{-\frac{ia\pi}2}$$
\begin{align}
I&=i\left(\frac{\pi}2-2\arctan e^{-\frac{ia\pi}2}\right)
\\&=i\left(\frac{\pi}2-\arctan e^{-\frac{ia\pi}2}–\arctan e^{-\frac{ia\pi}2}\right)
\\&=i\left(\arctan e^{\frac{ia\pi}2}-\arctan e^{-\frac{ia\pi}2}\right)
\\&=i\arctan\frac{e^\frac{ia\pi}2-e^{\frac{ia\pi}2}}{1+e^{\frac{ia\pi}2}e^{-\frac{ia\pi}2}}
\\&=i\arctan i\sin\frac{a\pi}2
\\&=-\mathrm{arctanh}\sin\frac{a\pi}2
\\&=\frac12\log\frac{\cos\frac{(1-a)\pi}2-1}{\cos\frac{(1-a)\pi}2+1}
\\&=\log\cot\frac{\pi(1-a)}{4}
\end{align}
でたーーー!!
留数定理気持ち良すぎだろ!!
おしまい!!
