【正の奇数が重複なくもれもなく現れる、コラッツ予想の計算を参照できる表】一般項に二変数をインプットして求めたコラッツ表をどうぞ！

103

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

コラッツ予想とは、こんな予想です↓

任意の正の整数ｎに対して、以下で定められる操作について考える。
・ｎが偶数の場合、ｎを２で割る
・ｎが奇数の場合、ｎに３をかけて１を足す
このとき、どんなｎから始めても、有限回の操作のうちに必ず１に到達する。

例えば、nが11であるときに、計算してみると・・・
11×3＋1=34
34÷2=17
17×3+1=52
52÷2=26
26÷2=13
13×3+1=40
40÷2=20
20÷2=10
10÷2=5
5×3+1=16
16÷2=8
8÷2=4
4÷2=2
2÷2=1

このコラッツの計算において、奇数だけを下のコラッツテーブル奇数表で答え合わせができます。
この奇数表では、s,tが自然数であるとき、正の奇数を表せます。
計算において、奇数の次の奇数をこの表で参照できます。奇数を表から見つけ、その列の上のピンクの文字が次の奇数です（グレー行の奇数の場合にはグレーの「6t-5」のピンク文字の数、ホワイト行の奇数の場合にはホワイトの「6t-1」のピンク文字の数を参照します）
奇数すべてを順にたどると、最後には必ず1に到達します。
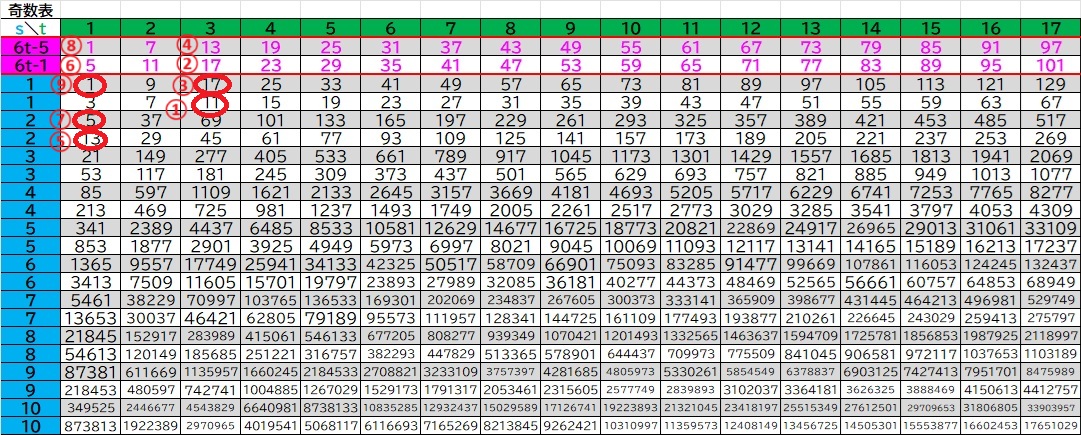コラッツテーブル奇数表