グリーン・タオの定理4　ハイパーグラフ除去補題の利用

こんにちは,itouです.
今回は前回確認した

の流れを

へと一般化したものを見ていきます.少しで分かりにくいと思ったら前回の記事を参照してください.以下で$k=3,r=2$としたものが前回の流れです.

定義

下のある図も参考にして下さい.直積や非交和が出てくるので,混同しないようにしてください.説明の都合上,一部私が導入した記号,用語が出てきます.

以下$J$を頂点集合の記号として用いますが,$J=[k]$として考えてもらってよいです.

$D_H$は私のオリジナルの記号です.$H$が($k$頂点)完全$r$グラフなら,$k$部$r$グラフデータに一致します.

$H=K^{(r)}_k$の場合は$E={J \choose r}$となります.

理解を助けるために,以下のように本書にはない用語を設定します.

$E$と$E_e$が出てきて紛らわしいですが,${J \choose r}$の部分集合が$E$で,$e\in E$によって$\sharp J$個の頂点小集合のうちどの$r$個を選ぶか指定し,その直積の部分集合を辺小集合$E_e$というのです.$D=((V_j)_{j\in J};(E_e)_{e\in E},(\varnothing)_{e\in {J \choose r}\backslash E})$とかいているのは,$H=K^{(r)}_k$の場合とは違って選んでいない$r$個の頂点小集合の組がある(つまり$ (\varnothing)_{e\in {J \choose r}\backslash E}$が空でない)からです.それら選んでいない辺を除いたのが$H$型の$k$部$r$グラフデータ$D_H=((V_j)_{j \in J};(E_e)_{e\in E})$です.

「三角形」に対応する言葉を導入しておきます.

$H(D_H)$は除去すべき$H$のコピーの頂点集合の集まりです.

イメージ

$k=4,r=3$の場合のイメージです.
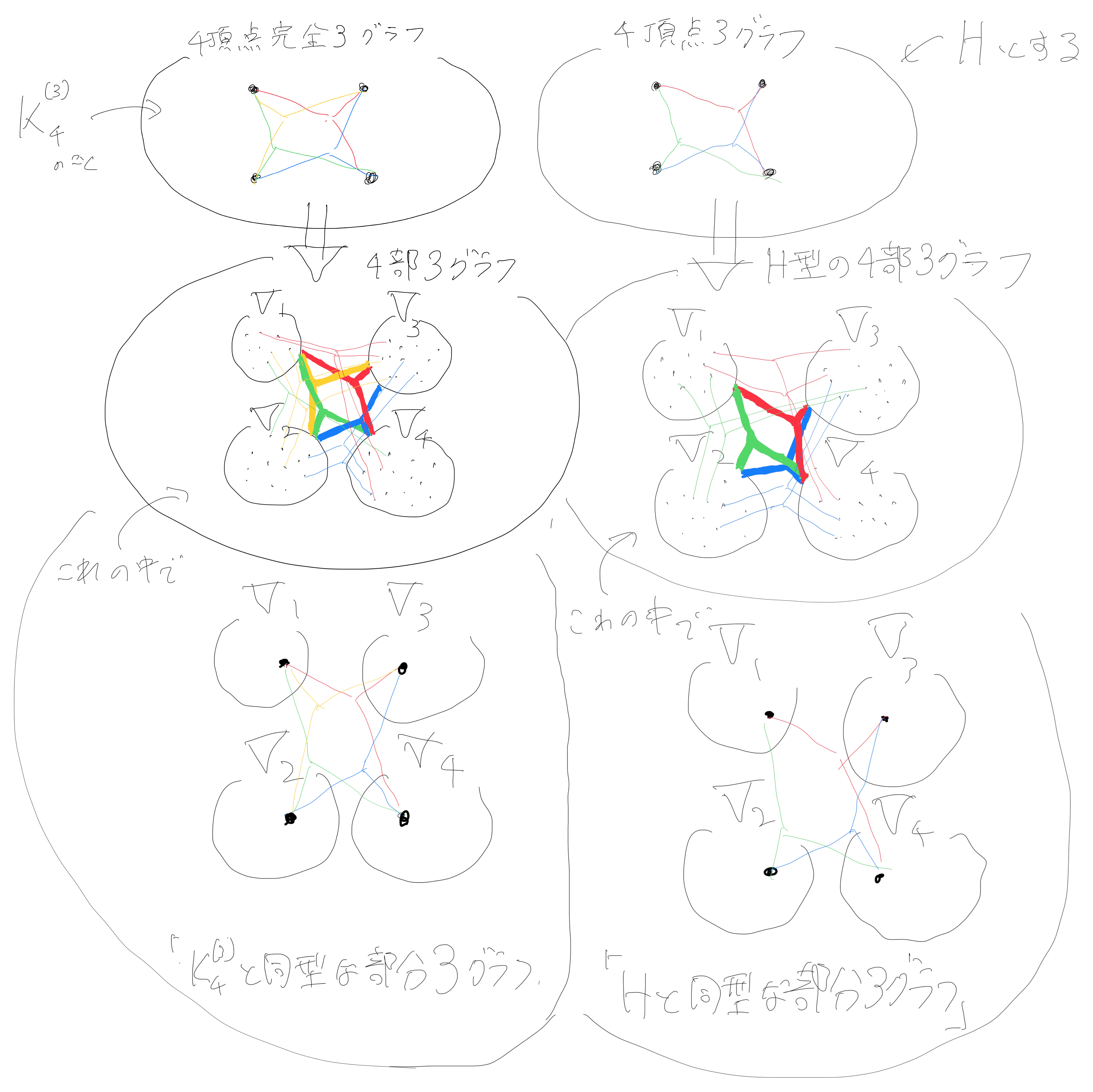イメージ

図中の「$K_4^{(3)}$と同型な部分3グラフ」が「$K_4^{(3)}$のコピー」,「$H$と同型な部分3グラフ」が「$H$のコピー」です.

本題

三角形除去補題と同様ハイパーグラフ除去補題にも2つのバージョンがありますが,以降単にハイパーグラフ除去補題と言ったら後者のグラフの言葉で書かれたものを指すことにします.

ハイパーグラフ除去補題$\Rightarrow$多次元コーナー定理

$r = 1$ならば多次元コーナー定理は自明.よって$r\geq 2$とします.実数$0<\delta \leq 1$を任意にとり,$N_{CT}(r,\delta)=\lceil\frac{1}{r}(\frac{1}{\delta'}+r-1)\rceil$と定義します.ただし,$\delta'=\delta_{PHRL}(r+1,\frac{\delta}{r^2+1})$.$N\geq N_{CT}(r,\delta)$とし,$\sharp A\geq \delta N^r$を満たす集合$A\subset [N]^r$をとります.

$A$からグラフをつくっていきます.
頂点集合については,各$j\in [r]$に対し,$V_j$を
\begin{align} V_j&=\{H_j(a):a\in [N]\} \\ \end{align}
と定義し,
\begin{align} V_{r+1}&=\{H_{r+1}(a):\in[r,rN]\} \\ \end{align}

とします.

ここで,$j\in [r]$のときは

\begin{align} H_{j}(a)&=\{(x_i)_{i\in[r]}\in \mathbb Z^r:x_j=a\} \\ \end{align}
$j=r+1$のときは
\begin{align} H_{r+1}(a)&=\{(x_i)_{i\in[r]}\in \mathbb Z^r:\sum_{i\in [r]}x_i=a\} \\ \end{align}

とします.$H_i(a)$は$\mathbb R^r$上の超平面の格子点からなる集合です.これを単に超平面ということにします.定義から$j\in [r]$のときは$\sharp V_j=N$,$\sharp V_{r+1}=rN-r+1$です.

辺集合を以下のようにしましょう.
$i\in [r+1]$ごとに$e_i=[r+1]\backslash \{i\}\in {[r+1]\choose r}$とおき,集合$E_{e_i}\subset \prod_{j\in e_i}V_j$を以下のように定義します.
$j\in e_i$ごとに超平面$H_j\in V_j$をとるとき,定義から$\bigcap_{j\in e_i}H_j$は1元集合です.そこで

\begin{align} (H_j)_{j\in e_i}\in E_{e_i}\Leftrightarrow \text{$\bigcap_{j\in e_i}H_j$は1元集合で$A$に含まれる} \end{align}

とします.まとめると,

このとき,集合$\mathcal H=K^{(r)}_{r+1}((V_j)_{j\in [r+1]};(E_{e_i})_{i\in [r+1]})$は,対応
\begin{align} (H_j(a_j))_{j\in [r+1]}\mapsto\left\{ (a_i)_{i\in[r]}+(a_{r+1}-\sum_{i\in [r]}a_i)\epsilon_j:j\in [r+1] \right\} \end{align}
によって,$A$に含まれる$r$次元コーナー全体の集合と1対1対応します.
ただし$\epsilon_i$は$r$次元の標準基底です(上から$i$番目の要素が1,他が0の列ベクトルを考えてください.$\epsilon_{r+1}$は0ベクトルとします).

前回同様$A$が非自明なコーナーを含むことを背理法で示しましょう.上の対応において$\mathcal H$の任意の元が自明な$r$次元コーナーに対応していると仮定します.

このとき,

\begin{align} \sharp\mathcal H=\sharp A\leq N^r\leq \delta_{PHRL}(r+1,\frac{\delta}{r^2+1})\prod_{j\in [r+1]}\sharp V_j \end{align}
であるので,ハイパーグラフ除去補題より,各$i\in [r+1]$に対して$E'_{e_i}\subset \prod_{j\in e_i}V_j $が存在して,$\mathcal H'=K^{(r+1)}_{r+1}((V_j)_{j\in [r+1]};(E'_{e_i})_{i\in [r+1]})=\varnothing$かつ任意の$i\in [r+1]$に対して
\begin{align} \sharp(E_{e_i}\backslash E'_{e_i})\leq \frac{\delta}{r^2+1}\prod_{j\in e_i}\sharp V_j \end{align}
が成立します.

ここで$D'_H=((V_j)_{j\in [r+1]};(E'_{e_i})_{i\in [r+1]})$は$r$グラフ型をすべて除去し終えたグラフです.
\begin{align} \sharp(E_{e_i}\backslash E'_{e_i}) \quad(i\in [r+1]) \end{align}
は除去すべき$r$グラフ型の個数のことです.

仮定は$\mathcal H$の任意の元が自明な$r$次元コーナーに対応していることを意味していました.$\mathcal H$の元である$r+1$個の超平面の組は,そのうちの$r$個から残りの1個が一意的に決まります.
よって次の写像:
\begin{align} \mathcal H\rightarrow\prod_{i\in[r+1]} (E_{e_{i}}\backslash E'_{e_{i}}) \end{align}
は単射です.

よって,
\begin{align} \sharp \mathcal H\leq\sum_{i\in[r+1]}\sharp(E_{e_{i_x}}\backslash E'_{e_{i_x}})\leq \frac{\delta}{r^2+1}\{(r^2+1)N^r-r(r-1)N\}<\delta N^r \end{align}
となりますが,これは$\sharp A \geq \delta N^r$に矛盾し,証明が完了します.

多次元コーナー定理$\Rightarrow$有限版多次元セメレディの定理に入る前に

本書では多次元コーナー定理$\Rightarrow$有限版多次元セメレディの定理の証明に,加群,短完全系列,切断といった用語を用いていますが,なるべくそれらを使わず説明します.(加群だけ使います)(これらの概念はこれより後には出てきませんし,この証明を理解するには大きすぎる牛刀といったところなので詳しくはやりません).ベクトル空間が分かれば十分です.

ベクトル空間の説明(高校数学の美しい物語)
ベクトル空間とは体$K$を用意して,$K$の元を係数として代数構造をつくったものです.この係数として用意する集合を体ではなく環$R$としたものを加群といいます.$R=\mathbb Z$のとき,$\mathbb Z-$加群といいます.このあとは$\mathbb Z-$加群しか出てきません.

1については$\mathbb Z^n$の 標準基底 をとることを考えるというだけです.

2については下の図を見て納得してください.
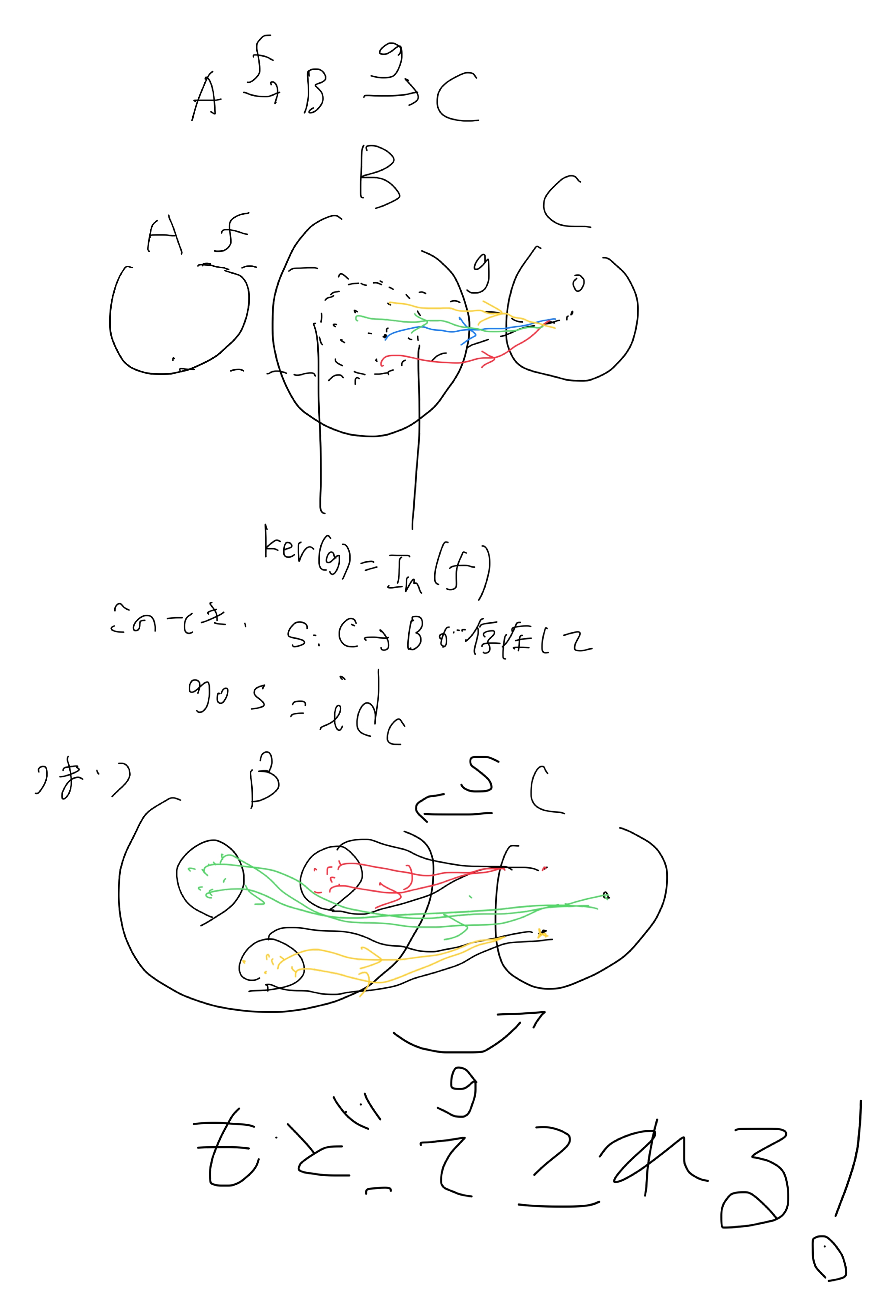短完全系列のイメージ
$C$より$B$の方が大きいので,$C$から$B$にいっても$C$に戻ってくることができるというだけです.

(星座の)標準形状というものを導入します.

星座の形状は標準形状であるとして一般性を失わないことを確認しましょう.というのも任意の星座$S$に対して,$S$に$0$が含まれていなければ$0$を追加し,さらに高々$d$個の元を付け加えることで,得られる集合$S'(\subset S)$が自由$\mathbb Z$加群を生成するようにします.すると$\tilde{S}=S'\cup(-S')$は標準形状なので,$ \tilde{S}$星座が目的の集合内に存在するならその部分集合として,$S$が含まれていることが示されます.よって標準形状の場合を考えて問題ありません.

多次元コーナー定理$\Rightarrow$有限版多次元セメレディの定理

さて,証明に入ります.標準形状$S\subset \mathbb Z^d$と実数$0<\delta \leq 1$を任意にとります.$r=\sharp S-1$とし,$S=\{s_1,\cdots,s_r,s_{r+1} \}$と元にインデックスを振っておきます.(ただし$s_{r+1}=0$)$\mathbb Z$加群の全射写像$\phi_S:\mathbb Z^r$を,各$i\in [r]$に対して$\phi_S(\epsilon_i)=s_i$として定めます.($(\epsilon_i)_{i\in \mathbb [r]}$は標準基底で$\epsilon_{r+1}$は0ベクトル)

このとき,集合の列:
$\ker(\phi_S)\rightarrow \mathbb Z^r \rightarrow \mathbb Z^d$
を考えます.

上で確認した通り,写像$\sigma:\mathbb Z^r \rightarrow \mathbb Z^d(g\circ \sigma=id _{\mathbb Z^d})$が存在します.1つ取って固定します.$\ker (\phi_S)$は$\mathbb Z-$加群$\mathbb Z^{r-d}$とみなすことができます.このことは$r$個の未知数に対し$d$個の関係式を与えれば,自由度が$r-d$になることよりわかります.
そのため基底$w_1,\cdots,w_{r-d}$をとることができ,$\sigma(\epsilon'_1),\cdots,\sigma(\epsilon'_d),w_1,\cdots,w_{r-d}$が$\mathbb Z^r$の基底となっていることが分かります.ただし,$(\epsilon'_i)_{i \in [d]}$は$\mathbb R^d$の標準基底です.
($\sigma(\epsilon'_1),\cdots,\sigma(\epsilon'_d),w_1,\cdots,w_{r-d}$が$\mathbb Z^r$が1次独立であることは,$\phi_S(w_i)=0$と$\phi_S(\sigma(\epsilon'_j))=\epsilon'_j$よりわかります).

この$\mathbb Z^r$の基底をなす$r$個のベクトルをそれぞれ基底$(\epsilon_i)_{i \in [r]} $に関して成分表示した際の各成分の絶対値の最大値の$r$倍を$U$とします.

すなわち,
\begin{align} \sigma(\epsilon'_i)&=\sum_{j\in [r]}x_j\epsilon_j\\ w_i&=\sum_{j\in [r]}y_j\epsilon_j\\ \end{align}
と成分表示するとき,$x_j,y_j$たちの中の絶対値の最大値の$r$倍を$U$とします.
そして,$N_{MST}(d,S,\delta)=\frac{1}{3U}N_{CT}(r,\frac{\delta}{(3U)^r})$と定めます.

$N\geq N_{MST}(d,S,\delta)$を満たす任意の整数$N$および$\sharp A\geq \delta N^d$であるような集合$A\subset [N]^d$をとります.$a\in [N]^d$に対して,
\begin{align} V(a)=\left\{ \sigma(a)+\sum_{i\in [r-d]} b_i w_i\in \mathbb Z^r:\forall i \in [r-d],b_i\in [N] \right\} \end{align}
とおきます.このとき,$\sharp V(a)=N^{r-d}$および$V(a)\subset \phi^{-1}_S(a)$が成り立っています.($\phi_S(w_i)=0$なので)

$\sigma (a)\in \mathbb Z^r$の$(\epsilon_i)_{i\in [r]}$に関する各成分の絶対値は$dUN/r$以下です.これは$a=\sum_{j\in [d]}a_j\epsilon'_j(a_j\in [N])$であるとき,$\sigma(a)=\sum_{j\in [d]}a_j\sigma(\epsilon'_j)$において,各$\sigma(\epsilon'_j)$をさらに$(\epsilon_i)_{i\in [r]}$に関する1次結合で表して展開すると,$a_j\leq N$と$d$倍することに注意してわかります.

同様に,$\sum_{i\in [r-d]}b_iw_i$に関する各成分の絶対値は$(r-d)UN/r$以下です.

以上により,$V(a)$の元の$(\epsilon_i)_{i\in [r]}$に関する各成分の絶対値は$dUN/r+(r-d)uN/r=UN$で上から抑えられます. よって,$ V(a)\subset [-UN,UN]^r$がわかりました.したがって,
\begin{align} \sharp (\phi^{-1}_S(a)\cap[-UN,UN]^r)\geq V(a)=N^{r-d} \end{align}
であり,$a\in A\subset [N]^d$なるすべての$a$にも上の不等式が成立するので,
\begin{align} \sharp (\phi^{-1}_S(A)\cap[-UN,UN]^r)\geq \sharp A\cdot N^{r-d} \end{align}
が示されました.$h=(UN+1)\sum_{i\in [r]}\epsilon_i\in \mathbb Z^r$とし,
\begin{align} B=h+(\phi^{-1}_S(A)\cap[-UN,UN]^r) \end{align}
として$B$を定めると,$B\subset [2UN+1]^r\subset [3UN]^r$
となっています.および$A$に関する条件から,
\begin{align} \sharp B\geq \sharp A\cdot N^{r-d}\geq \delta N^r=\frac{\delta}{(3U)^r}\cdot (3UN)^r \end{align}
とできます.$3UN\geq N_{CT}(r,\frac{\delta}{(3U)^r})$なので,
多次元コーナー定理(定理3のステートメントで$\delta$を$\frac{\delta}{(3U)^r}$,$N$を$(3UN)^r$とした)より,$B$は非自明な$r$次元コーナー$\{a+l\epsilon_i:i \in[r+1] \}(a\in \mathbb Z^r,l \in\mathbb Z\backslash\{0\})$を含みます.これを$\phi_S$で$\mathbb Z$で射影すると,$A$が$\{\phi_S(a-h)+ls_i:i\in [r+1]\}=\phi_S(a-h)+lS$を含むことがわかります.$l$は負である可能性もありますが,$S=-S$であったので,これは$S$星座です.

これで多次元コーナー定理$\Rightarrow$有限版多次元セメレディの定理
も示されました.

感想

結構大変でした.次はいよいよハイパーグラフ除去補題の証明にとりかかります.30ページぐらいあるので,一部を解説するだけになるかも.やる気次第です.

謝辞

ここまで読んで下さりありがとうございました。誤植等指摘お願いいたします.