文献あり

ポンスレ束について

1033

はじめに

　初等幾何について調べていると,「～双曲線」なるものに出合うことがあります. 例えば, フェルマー点やナポレオン点の拡張であるキーペルトの定理に関連して, キーペルト双曲線というものが知られています. また, フォイエルバッハの定理などに関連して, ジェラベク双曲線やフォイエルバッハ双曲線というものも知られています.
　実はこれらは全てポンスレ束というグループに属しており, 等角共役やシムソン線と深い関わりがあります. この記事では, 初等幾何の側面からこれらの双曲線について紹介します.

等角共役とその性質

等角共役の定義

等角共役

内心を $I$ とする三角形 $A B C$ と点 $P$ をとる. このとき, 直線 $A I, B I, C I$ に関して $A P, B P, C P$ と対称な直線は1点で交わる. この交点を $P$ の等角共役 (isogonal conjugate)という.（断りがない限り, この記事では $P$ の等角共役を $P^{'}$ で表す.）

　証明は『等角共役点とその証明』などを参考にしてください. 以下, $P$ が特殊な位置にある場合の $P^{'}$ について考えます.

辺上にあるとき

　 $P$ が三角形 $A B C$ の辺上にあるとき, $P^{'}$ は頂点に一致します. 例えば, $P \neq B, C$ が $B C$ 上にあるとき, $P^{'} = A$ となります. これは等角共役の定義からすぐに分かります.

頂点に一致するとき

　 $P$ が三角形 $A B C$ の頂点に一致するとき, $P^{'}$ は定義されません. 実際, $P = A$ のとき直線 $A P$ なんてものは取れません.

外接円上にあるとき

　 $P$ が円 $A B C$ 上にあるとき, $A P, B P, C P$ を対称移動させた直線は全て平行になります. 従って, $P^{'}$ はこの平行線から定まる無限遠点です.
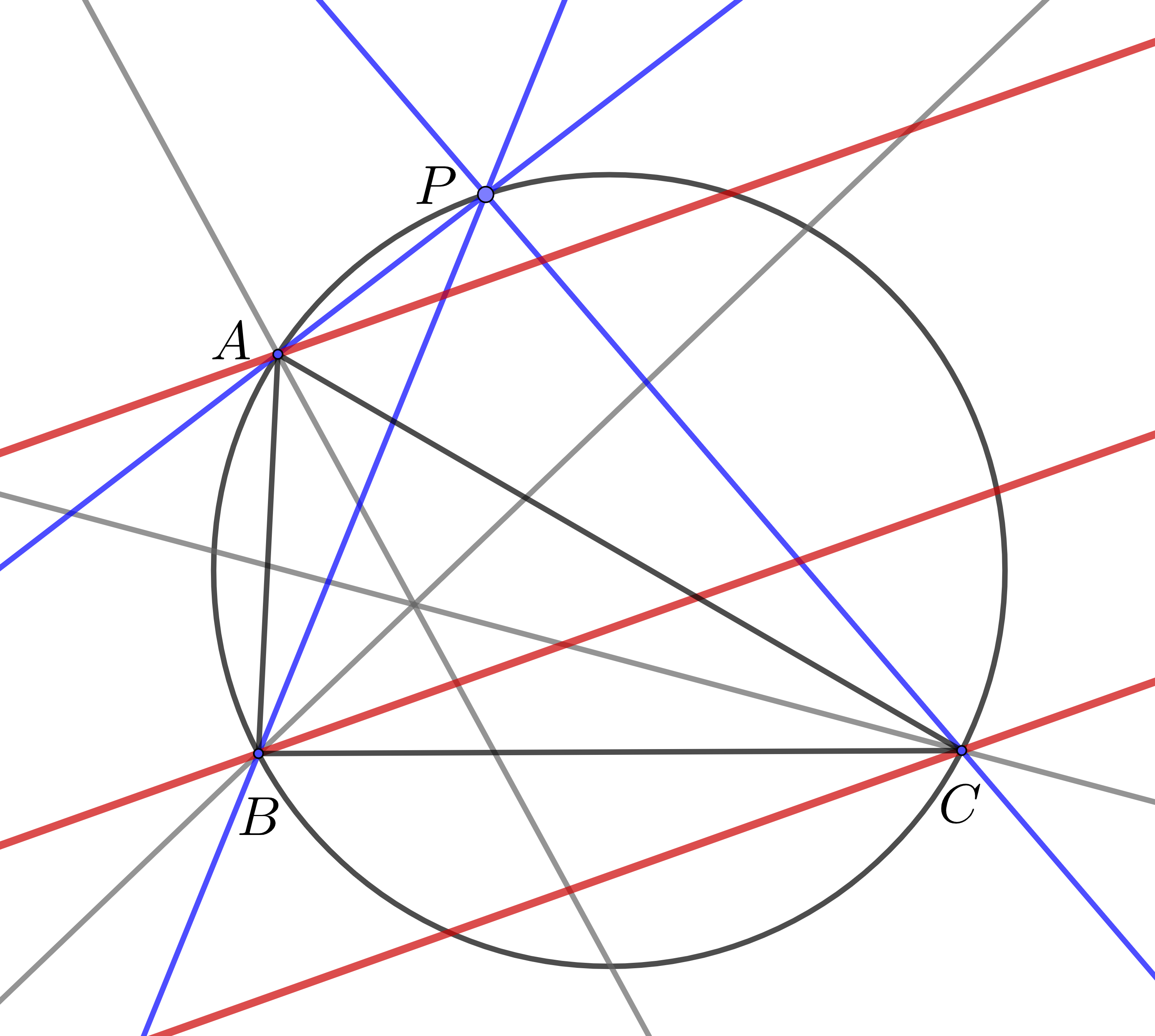　赤線の方向の無限遠点に移る

無限遠点のとき

　等角共役は2回施すと元に戻るので, 上と逆のことをすれば無限遠点の等角共役を定めることができ, これは円 $A B C$ 上に乗ります.

　以上より, 等角共役は $A, B, C$ を除外した射影平面上で定義される写像とみなせます.

等角共役点をつくる

　2組の等角共役点があったとき, そこから新たに等角共役な2点の組を作ることができます. これは主定理の証明で使います.

三角形 $A B C$ と相異なる2点 $P, Q$ に対し, $X = P Q \cap P^{'} Q^{'}, Y = P Q^{'} \cap P^{'} Q$ は互いに等角共役である.

$P = [p_{1} : p_{2} : p_{3}], Q = [q_{1} : q_{2} : q_{3}]$ とすると, $P Q^{'}, P^{'} Q$ の方程式はそれぞれ次のように表せる.
$P Q^{'} : | \begin{matrix} p_{1} & p_{2} & p_{3} \\ a^{2} q_{2} q_{3} & b^{2} q_{3} q_{1} & c^{2} q_{1} q_{2} \\ x & y & z \end{matrix} | = 0$
$P^{'} Q : | \begin{matrix} q_{1} & q_{2} & q_{3} \\ a^{2} p_{2} p_{3} & b^{2} p_{3} p_{1} & c^{2} p_{1} p_{2} \\ x & y & z \end{matrix} | = 0$

上の2式を連立して, $Y = [y_{1} : y_{2} : y_{3}]$ とすると, 次を得る.
$\begin{aligned} y_{1} = (b^{2} p_{1} q_{1} - a^{2} p_{2} q_{2}) (a^{2} p_{3} q_{3} - c^{2} p_{1} q_{1}) (p_{3} q_{2} - p_{2} q_{3}) \\ y_{2} = (c^{2} p_{2} q_{2} - b^{2} p_{3} q_{3}) (b^{2} p_{1} q_{1} - a^{2} p_{2} q_{2}) (p_{1} q_{3} - p_{3} q_{1}) \\ y_{3} = (a^{2} p_{3} q_{3} - c^{2} p_{1} q_{1}) (c^{2} p_{2} q_{2} - b^{2} p_{3} q_{3}) (p_{2} q_{1} - p_{1} q_{2}) \end{aligned}$

$Y$ の等角共役は,
$Y^{'} = [\frac{a^{2} (c^{2} p_{2} q_{2} - b^{2} p_{3} q_{3})}{p_{3} q_{2} - p_{2} q_{3}} : \frac{b^{2} (a^{2} p_{3} q_{3} - c^{2} p_{1} q_{1})}{p_{1} q_{3} - p_{3} q_{1}} : \frac{c^{2} (b^{2} p_{1} q_{1} - a^{2} p_{2} q_{2})}{p_{2} q_{1} - p_{1} q_{2}}]$ である.

このとき,
$| \begin{matrix} y_{1}^{'} & y_{2}^{'} & y_{3}^{'} \\ p_{1} & p_{2} & p_{3} \\ q_{1} & q_{2} & q_{3} \end{matrix} | = 0, | \begin{matrix} y_{1}^{'} & y_{2}^{'} & y_{3}^{'} \\ a^{2} p_{2} p_{3} & b^{2} p_{3} p_{1} & c^{2} p_{1} p_{2} \\ a^{2} q_{2} q_{3} & b^{2} q_{3} q_{1} & c^{2} q_{1} q_{2} \end{matrix} | = 0$
であるから, 3点 $Y^{'}, P, Q$ と $Y^{'}, P^{'}, Q^{'}$ はそれぞれ共線. よって $X = Y^{'}$ より主張は従う.

直線の等角共役

　直線上を動く点の等角共役はある円錐曲線上を動きます. かなり非自明な性質ですが, 重心座標で表せば一発です.

等角共役による直線の像

三角形 $A B C$ と $A, B, C$ を通らない直線 $l$ 上の点 $P$ をとる. $P$ が $l$ 上を動くとき, $P^{'}$ の軌跡は $A B C$ に外接する円錐曲線となる.

重心座標において等角共役は $[x : y : z] \mapsto [a^{2} y z : b^{2} z x : c^{2} x y]$ と表現できる. $m$ の方程式を $p x + q y + r z = 0$ とすれば, $m$ の像は $p a^{2} y z + q b^{2} z x + r c^{2} x y = 0$ と表せ, これは円錐曲線の形なのでよい.

　さらに, 移した先の円錐曲線の形状は外接円と $l$ の交点の個数により判別できます.

定理2

$l$ の像として現れる円錐曲線の形状は次のように判別できる.

$l$ が円 $A B C$ と交わらないとき, 楕円（ $l$ が無限遠直線のとき, 円）
$l$ と円 $A B C$ が接するとき, 放物線
$l$ と円 $A B C$ が2点で交わるとき, 双曲線

外接円上の点の等角共役は無限遠点であるから, 円 $A B C$ と $l$ の共有点の個数と $l$ の像が通る無限遠点の個数が一致する.

GeoGebraで表示した!FORMULA[67][1150601][0]の軌跡 GeoGebraで表示した $P^{'}$ の軌跡

ポンスレ束

　漸近線が直交する双曲線を直角双曲線といいます. まず初等幾何で直角双曲線を扱う際にとても重要となる補題を示します.

共線でない3点 $A, B, C$ を通る双曲線 $H$ について, 以下は同値.
(1) $H$ は直角双曲線である
(2) 三角形 $A B C$ の垂心は $H$ 上にある

　この補題は, ブリアンションとポンスレによるパスカルの定理を用いた簡潔な証明が知られています. 以下は[4]-p.299の証明です.

逆も同様なので, (1) $\Rightarrow$ (2)のみ示す.
$C$ を通りABに垂直な直線が $H$ と再び交わる点を $D$ とし, $H$ の漸近線方向の無限遠点を $E, F$ とする.
$H = A B \cup D E, K = C D \cup F A$ として6点 $A, B, C, D, E, F$ にパスカルの定理を用いると, $K H ∥ B C$ を得る.
$K$ は三角形 $A D H$ の垂心なので, $A D ⊥ B C$ を得る. よって, $D$ は三角形 $A B C$ の垂心であり, 主張は示された.

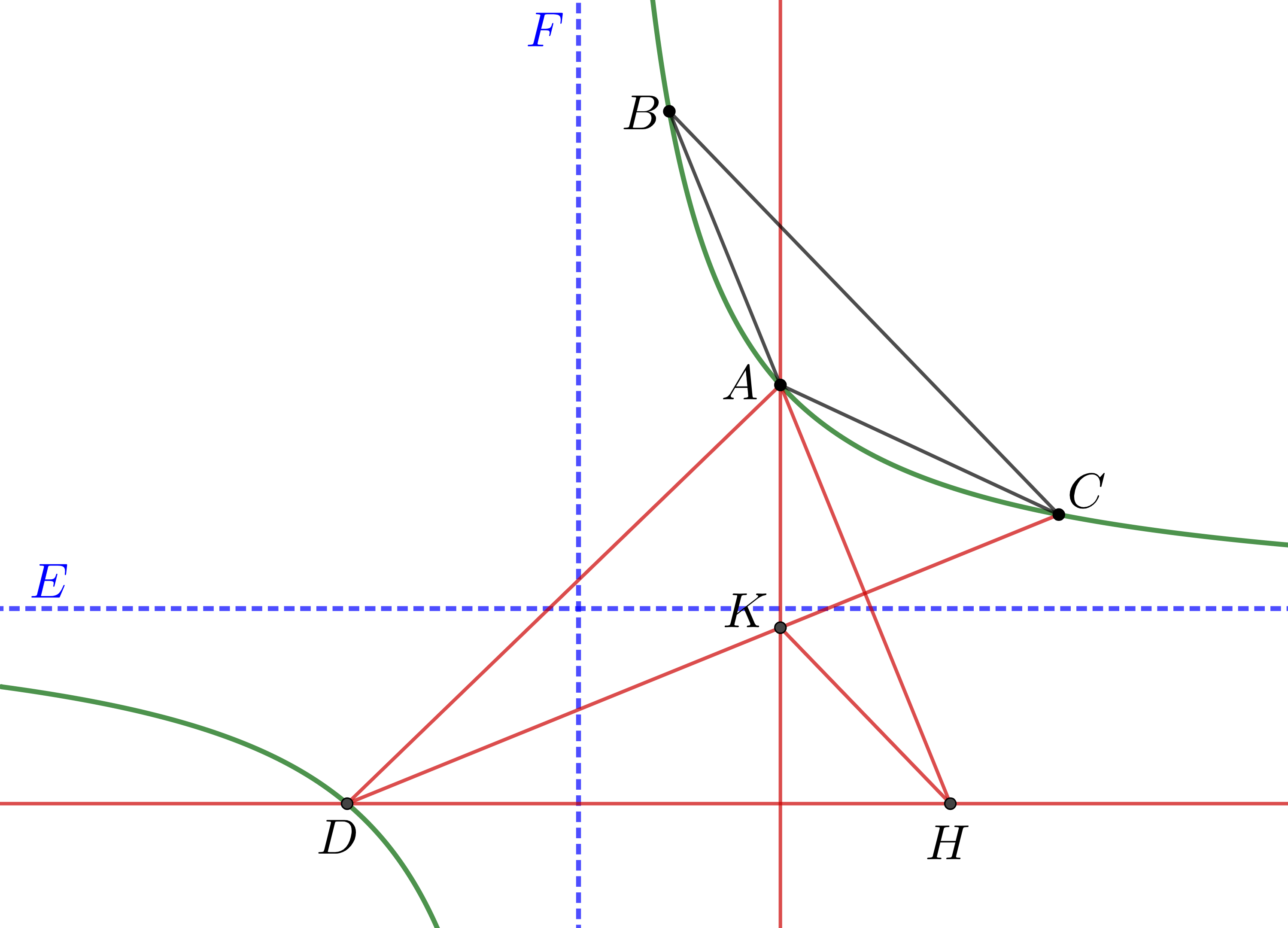直角双曲線と垂心

　簡単な角度追跡により, 外心と垂心は等角共役の関係にあることがわかります. 従って, 外心を通る直線の等角共役は直角双曲線になり, 次のようにポンスレ束が定義できます.

ポンスレ束

三角形 $A B C$ において, 外心 $O$ を通り, $A, B, C$ を通らない直線 $l$ の等角共役は $A B C$ に外接する直角双曲線となる. このような $l$ の等角共役として得られる直角双曲線全体の集合をポンスレ束(Poncelet pencil)という.

　 $l$ が三角形の頂点を通る場合, $l$ の等角共役は（正確にはある1点を除いた）直線となるので考えないことにします.
　さて, ポンスレ束の仲間たちをいくつか紹介しておきましょう. 以下, $I, O, H, K$ でそれぞれ三角形 $A B C$ の内心・外心・垂心・類似重心を表します.

フォイエルバッハ双曲線

　フォイエルバッハ双曲線(Feuerbach hyperbola)は, $O I$ の等角共役として得られる双曲線です. フォイエルバッハ双曲線の中心はフォイエルバッハ点（内接円と9点円の接点）であり, ジェルゴンヌ点・ナーゲル点を通ることが知られています. また, $I$ は等角共役で不動なのでフォイエルバッハ双曲線は $I$ で $O I$ に接します. ([3]を参照)

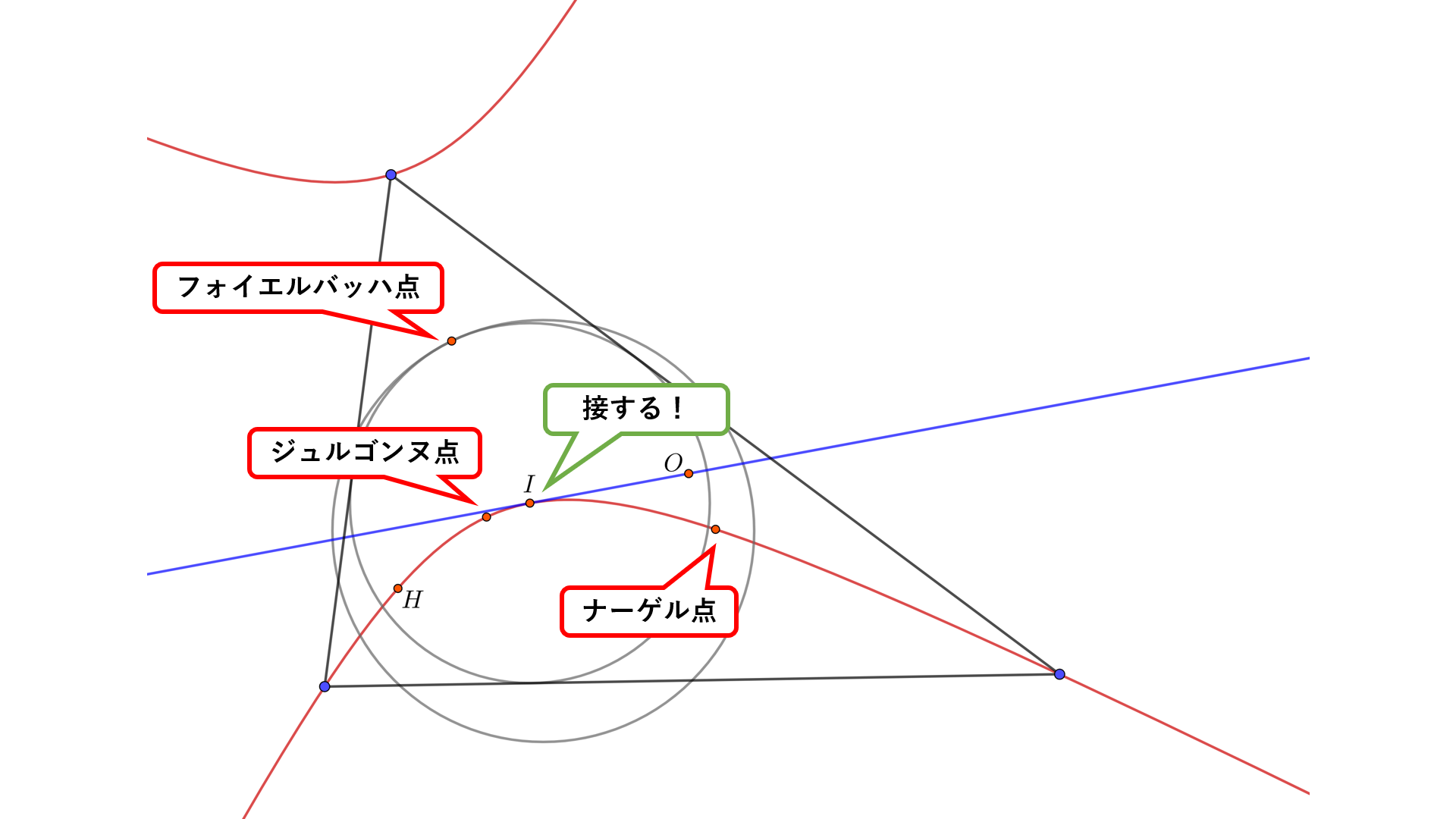フォイエルバッハ双曲線

キーペルト双曲線

　キーペルト双曲線(Kiepert hyperbola)は, $O K$ の等角共役として得られる双曲線です. シュピーカー中心（3つの傍接円の根心）を通ることが知られています. ([3]を参照) 　

ジェラベク双曲線

　ジェラベク双曲線(Jerabek hyperbola)は, $O H$ , つまりオイラー線の等角共役として得られる双曲線です. ジェラベク双曲線と三角形 $A B C$ の外接円の第4の交点は, 円 $A B C$ における「オイラー線の反シュタイナー点」の対蹠点になります. ([3]を参照)

中心及び漸近線の特徴づけ

　これまでみてきたように, ポンスレ束に属する具体的な双曲線は様々な初等幾何の定理と密接に関わっています. では, 一般に三角形に外接する直角双曲線自体にはどのような初等幾何的性質があるのでしょうか?
　驚くべきことに, ポンスレ束に属する直角双曲線の漸近線の正体はシムソン線なのです. というわけでシムソン線との関係を示してこの記事を終わりにしたいと思います.

主定理

三角形 $A B C$ とその外接円の直径 $P Q$ をとり, 直線 $P Q$ の等角共役を $H$ とする. このとき, $H$ の中心は9点円上にあり, 漸近線は $P, Q$ におけるシムソン線に一致する.

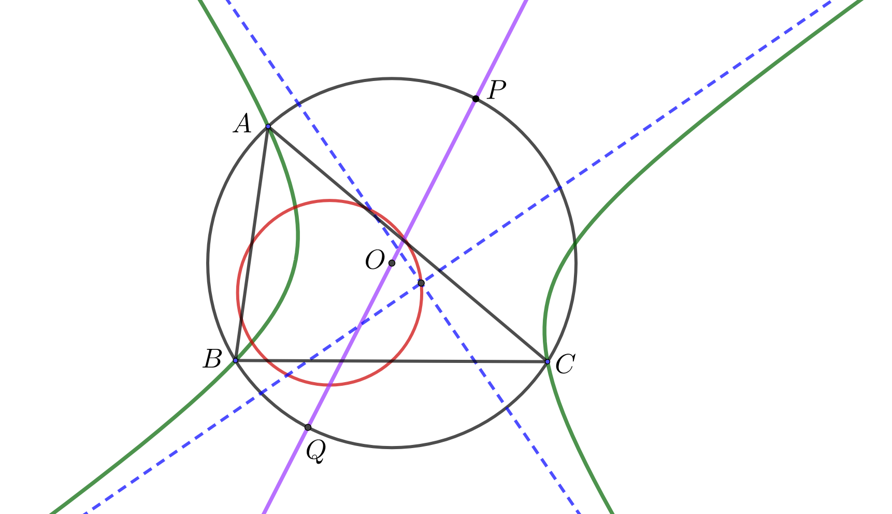ポンスレ束の双曲線とその漸近線

$P Q$ の等角共役を $H$ とし, $H$ と円 $A B C$ の第4の交点を $D$ と定める.
次の3ステップに分けて主定理を証明する.
(1) $H$ の中心は $D H$ の中点
(2) $P^{'}, Q^{'}$ はそれぞれ $Q, P$ におけるシムソン線方向の無限遠点
(3) $P, Q$ におけるシムソン線は $D H$ の中点を通る

はじめに(1)を示す. 三角形 $B C D$ の垂心を $H_{1}$ とすると, 補題4よりこれは $H$ 上にある.
$B C$ について $H, H_{1}$ と対称な点はそれぞれ円 $A B C$ 上にあるから, $A H H_{1} D$ は平行四辺形である. よって, $D, H$ は $H$ の中心について対称な点とわかるので主張は従う.
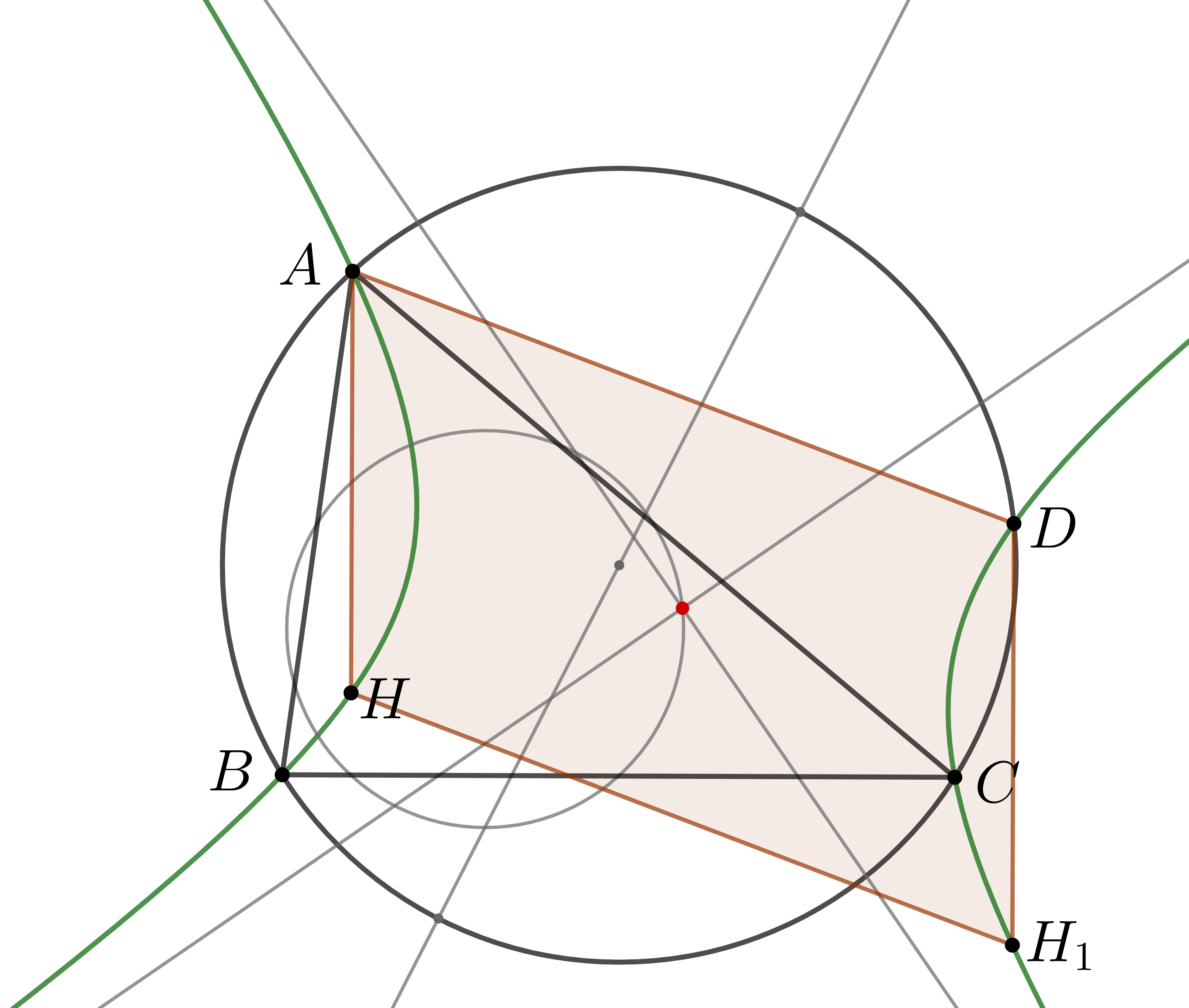(1)の証明

次に(2)を示す. $Q$ を通り $B C$ に垂直な直線と円 $A B C$ が再び交わる点を $R$ とすると, 『シムソン線であそぼう！』の命題3より, $A R$ は $Q$ におけるシムソン線に平行である. 一方, $A P$ と $A R$ は $∠ A$ の二等分線について対称なので, $P^{'}$ は $Q$ におけるシムソン線方向の無限遠点である. 同様にして, $Q^{'}$ は $P$ におけるシムソン線方向の無限遠点であることも言えるので, 主張は示された.

最後に(3)を示す. $P, Q$ に補題2を用いると, $X = P Q \cap P^{'} Q^{'}$ と $Y = P Q^{'} \cap P^{'} Q$ は互いに等角共役である. $X$ は $P Q$ 方向の無限遠点であるから, $Y = D$ を得る. よって, $P D, Q D$ は $P, Q$ におけるシムソン線にそれぞれ平行である. 一方, 『シムソン線であそぼう！』の命題4より, $P, Q$ におけるシュタイナー線は定点 $H$ を通る. よって, $P, Q$ におけるシムソン線は $D H$ の中点を通るので, これは漸近線に他ならない. 以上より主定理は示された.
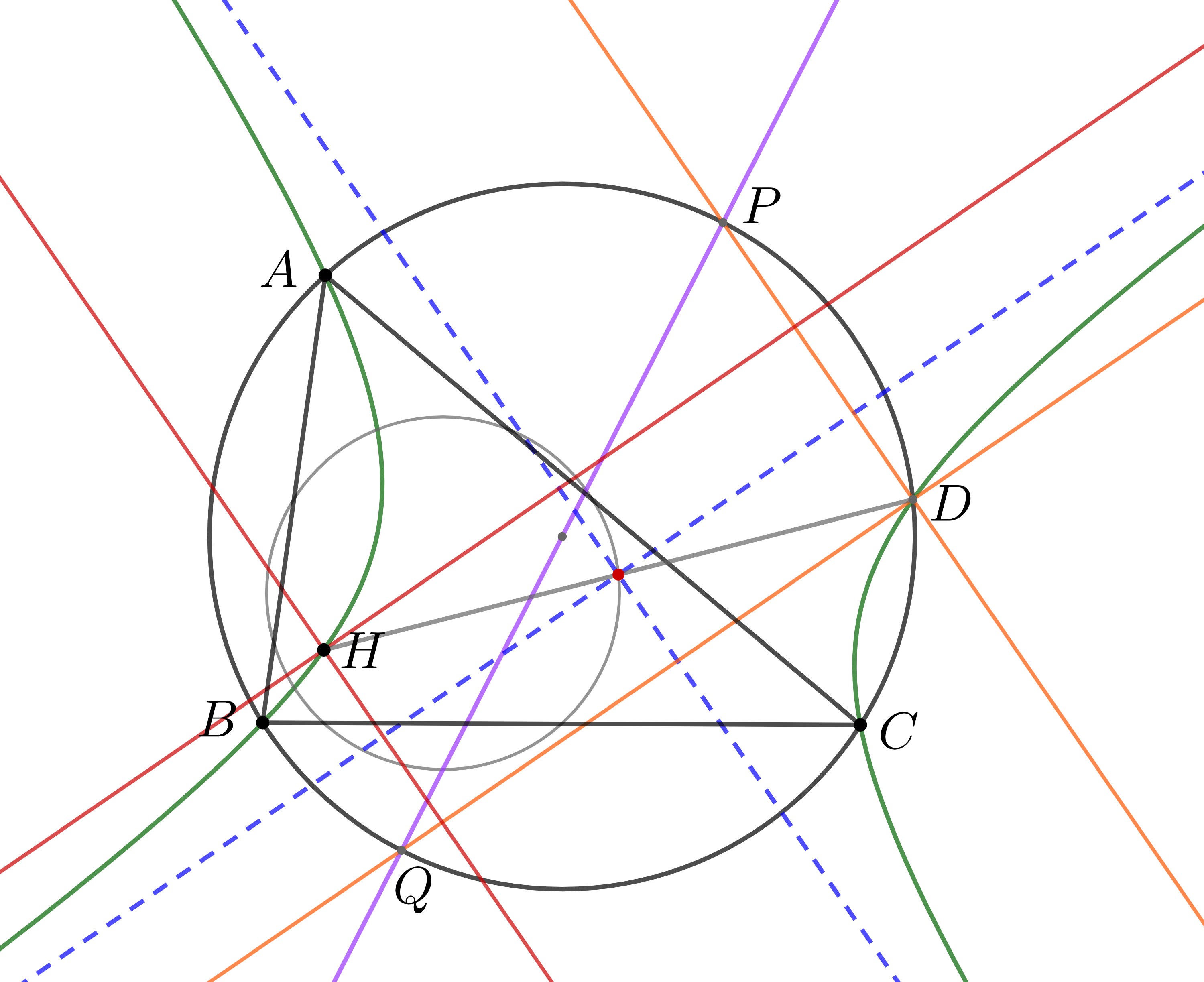漸近線など