文献あり

シムソン線であそぼう！

2266

シムソンの定理・シュタイナーの定理

　まずはこの記事の主役であるシムソン線とシュタイナー線を導入します. 証明中に出てくる有向角についてはこちらの記事 [3]を参照してください.

シムソンの定理

三角形 $A B C$ とその外接円上に点 $D$ をとる. $D$ から直線 $B C, C A, A B$ に下した垂線の足をそれぞれ $P, Q, R$ とするとき, この3点は共線である. この直線をシムソン線(Simson line)という.

次のように角度計算できる.
$∡ Q P R = ∡ Q P D + ∡ D P R = ∡ Q C D + ∡ D B R = ∡ A C D + ∡ D B A = 0$

　高校数学の美しい物語では複素座標でも証明されています.

シュタイナーの定理

三角形 $A B C$ とその外接円上に点 $D$ をとる. 直線 $B C, C A, A B$ に対して $D$ と対称な点をそれぞれ $P, Q, R$ とするとき, この3点は共線である. この直線をシュタイナー線(Steiner line)という.

シュタイナー線はシムソン線を2倍に相似拡大したものなので明らか.

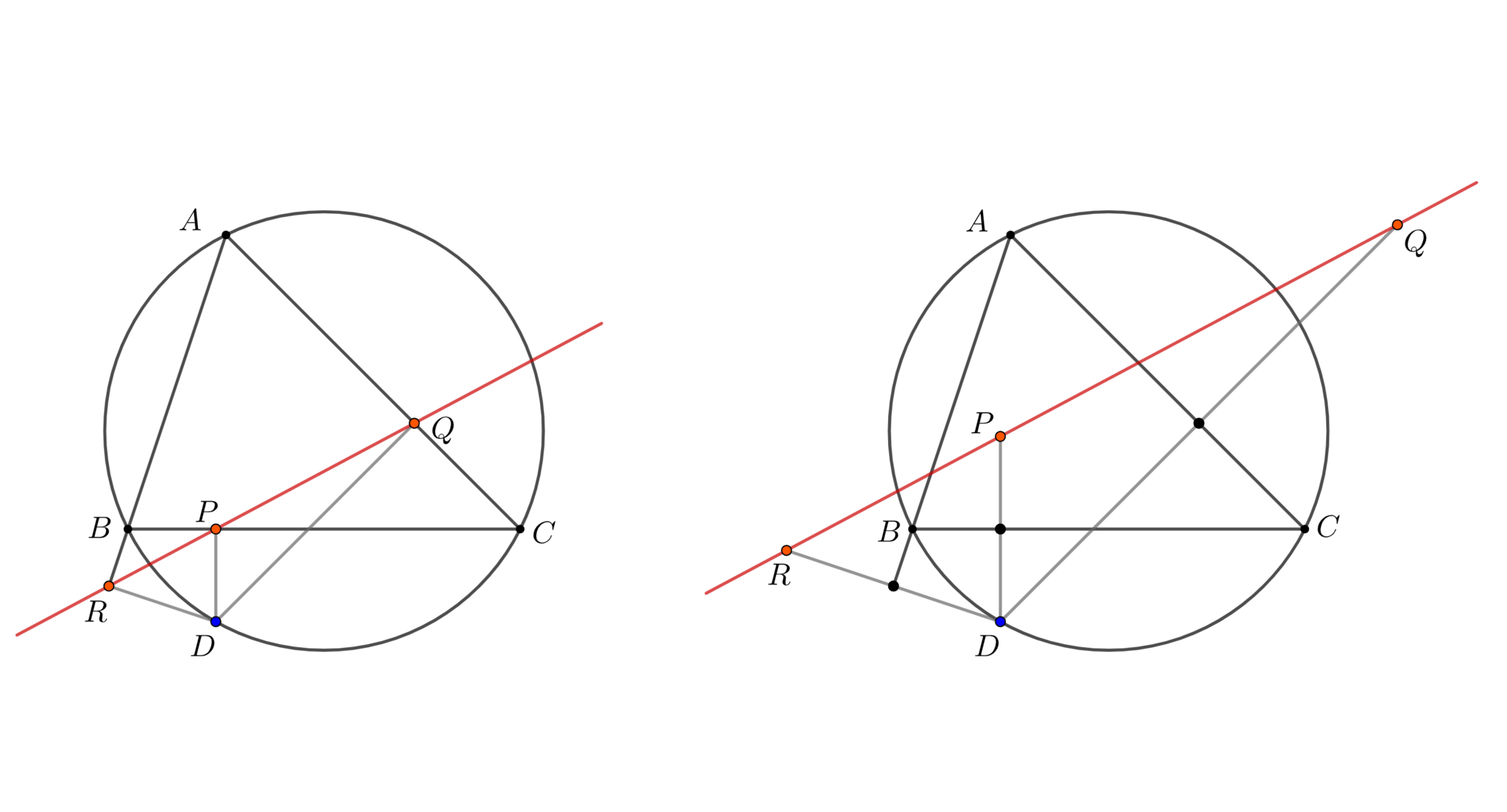シムソン線とシュタイナー線

シムソン線周りの構図

　この章では, シムソン線に関連する構図をいくつか紹介します. 構図と言っても数オリで使えるわけではなさそうです.

シムソン線に平行な直線

三角形 $A B C$ とその外接円上に点 $D$ をとる. $D$ を通り $B C$ に垂直な直線が外接円と再び交わる点を $D^{'}$ とすると, $A D^{'}$ は $D$ におけるシムソン線に平行である.

定理1と同様に $P, Q, R$ を定める.
$∡ A D^{'} P = ∡ A D^{'} D = ∡ A C D = ∡ Q C D = ∡ Q P D = ∡ Q P D^{'}$
よりよい.

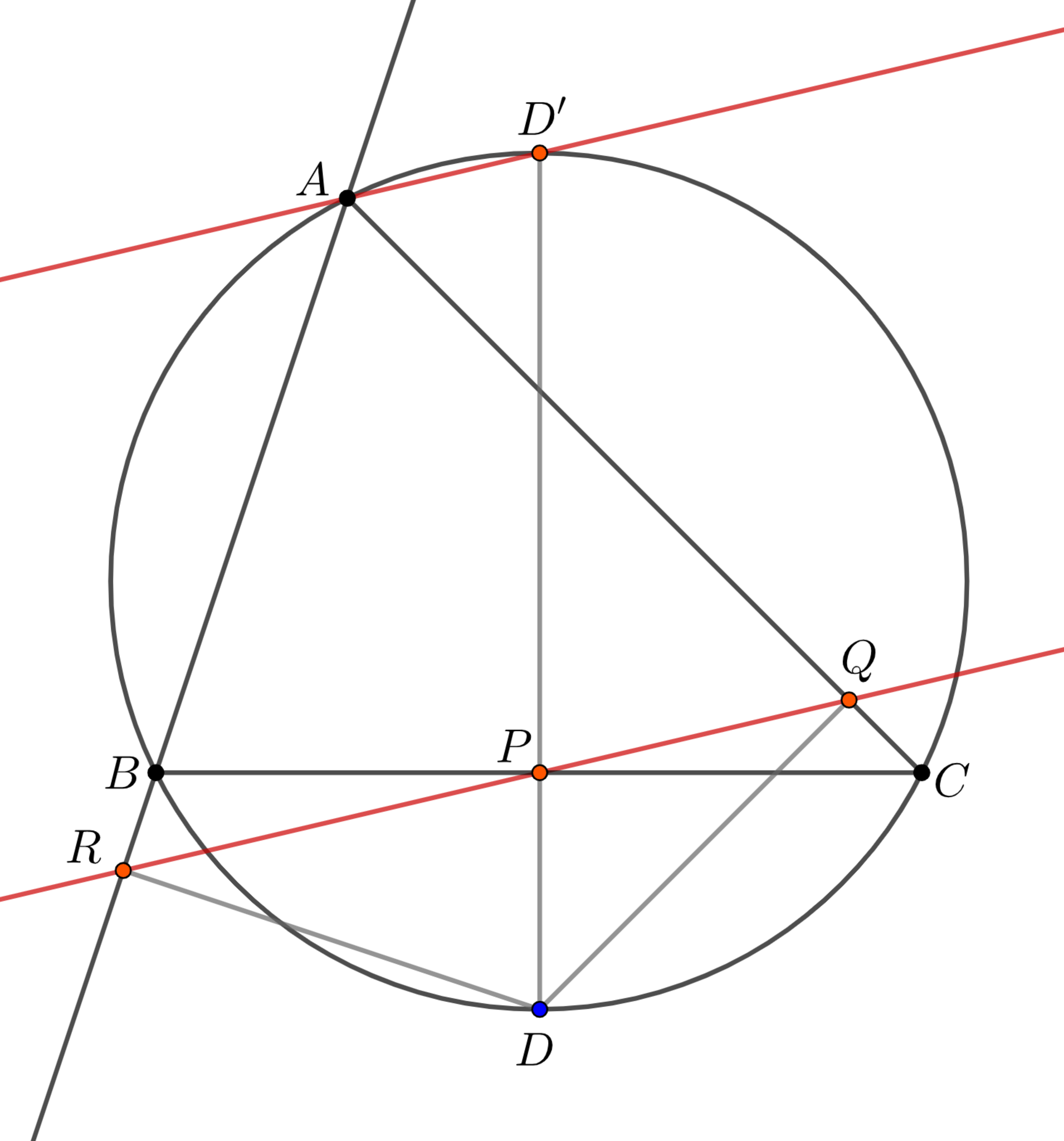シムソン線に平行な直線

シムソン線と垂心

シュタイナー線と垂心

垂心を $H$ とする三角形 $A B C$ とその外接円上に点 $D$ をとる. このとき, $D$ におけるシュタイナー線は $H$ を通る.

定理2と同様に $P, Q, R$ を定め, 三角形 $A B C$ の外接円を $Γ$ とする. $B C, C A, A B$ について $H$ と対称な点は $Γ$ 上にあるから, $B C, C A, A B$ について $Γ$ と対称な円 $Γ_{A}, Γ_{B}, Γ_{C}$ はすべて $H$ を通り, $P, Q, R$ はそれぞれこれらの円上にある. よって, 次が成り立つ.
$∡ Q H R = ∡ Q H C + ∡ C H B + ∡ B H R = ∡ Q A C + ∡ B A C + ∡ B A R = ∡ C A D + ∡ B A C + ∡ D A B = 0$
よって, 3点 $Q, R, H$ は共線であり, $H$ はシュタイナー線上にある.

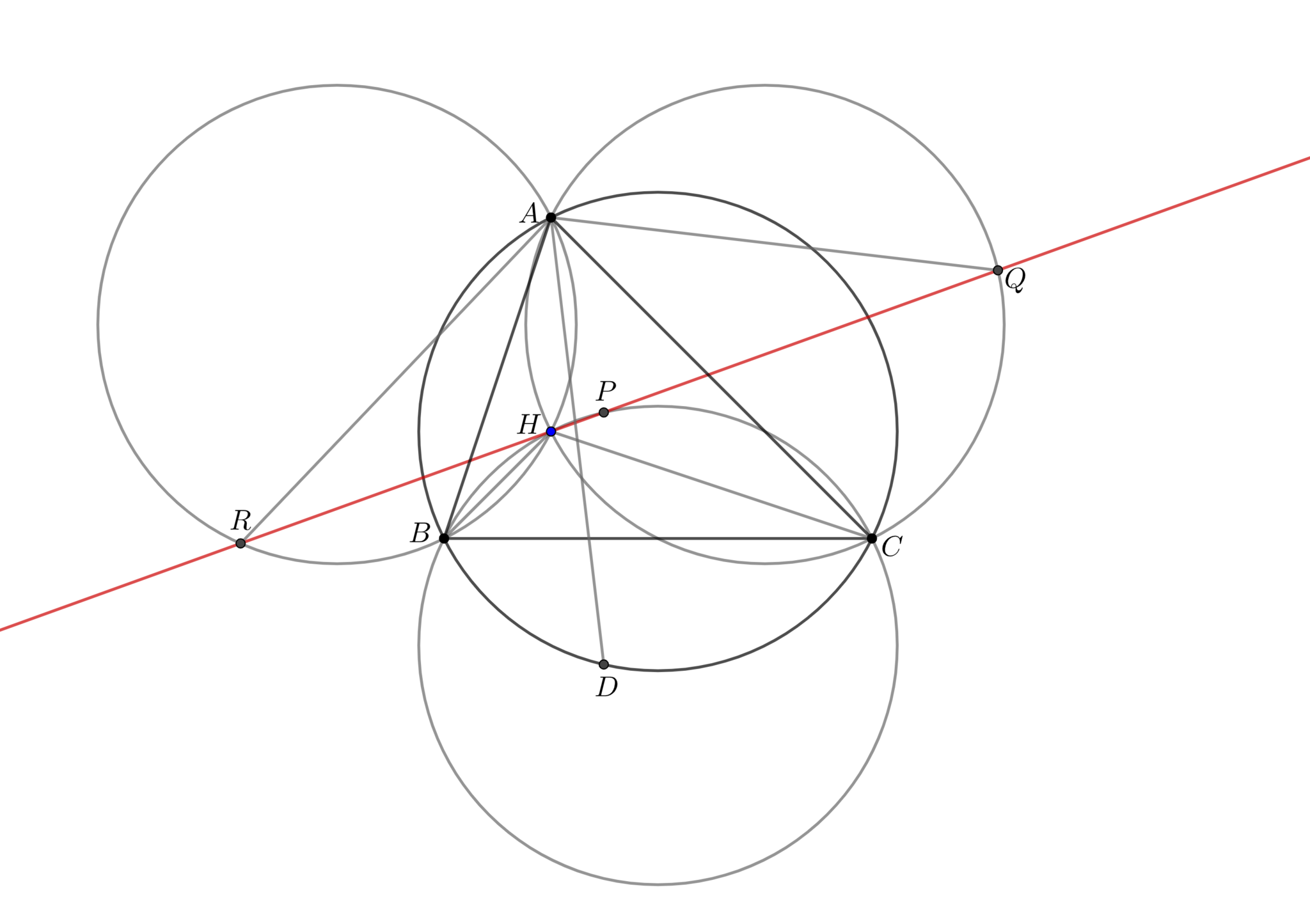垂心を通るシュタイナー線

　EGMO(p.59)では, 命題4は別の方法で（命題3を用いて）証明されています. 気になる方は参照してください. 命題4とは逆に, $H$ を通る任意の直線はある点におけるシュタイナー線になることが知られています. それが次の命題5です.

反シュタイナー点

垂心を $H$ とする三角形 $A B C$ と $H$ を通る直線 $m$ をとる. このとき, $B C, C A, A B$ について $m$ と対称な直線は外接円上の1点で交わる. この点を $m$ の反シュタイナー点(Anti-Steiner point))という.

$B C, C A, A B$ について $H$ と対称な点をそれぞれ $H_{A}, H_{B}, H_{C}$ とし, $m$ と対称な直線をそれぞれ $m_{A}, m_{B}, m_{C}$ とする. $m_{A}$ と $Γ$ の $H_{A}$ 以外の交点を $D$ とすると, $m$ は $D$ におけるシュタイナー線である. よって, $D H_{B}, D H_{C}$ はそれぞれ $C A, A B$ について $m$ と対称な直線であるから, $m_{B}, m_{C}$ は $D$ を通る. よって主張は示された.

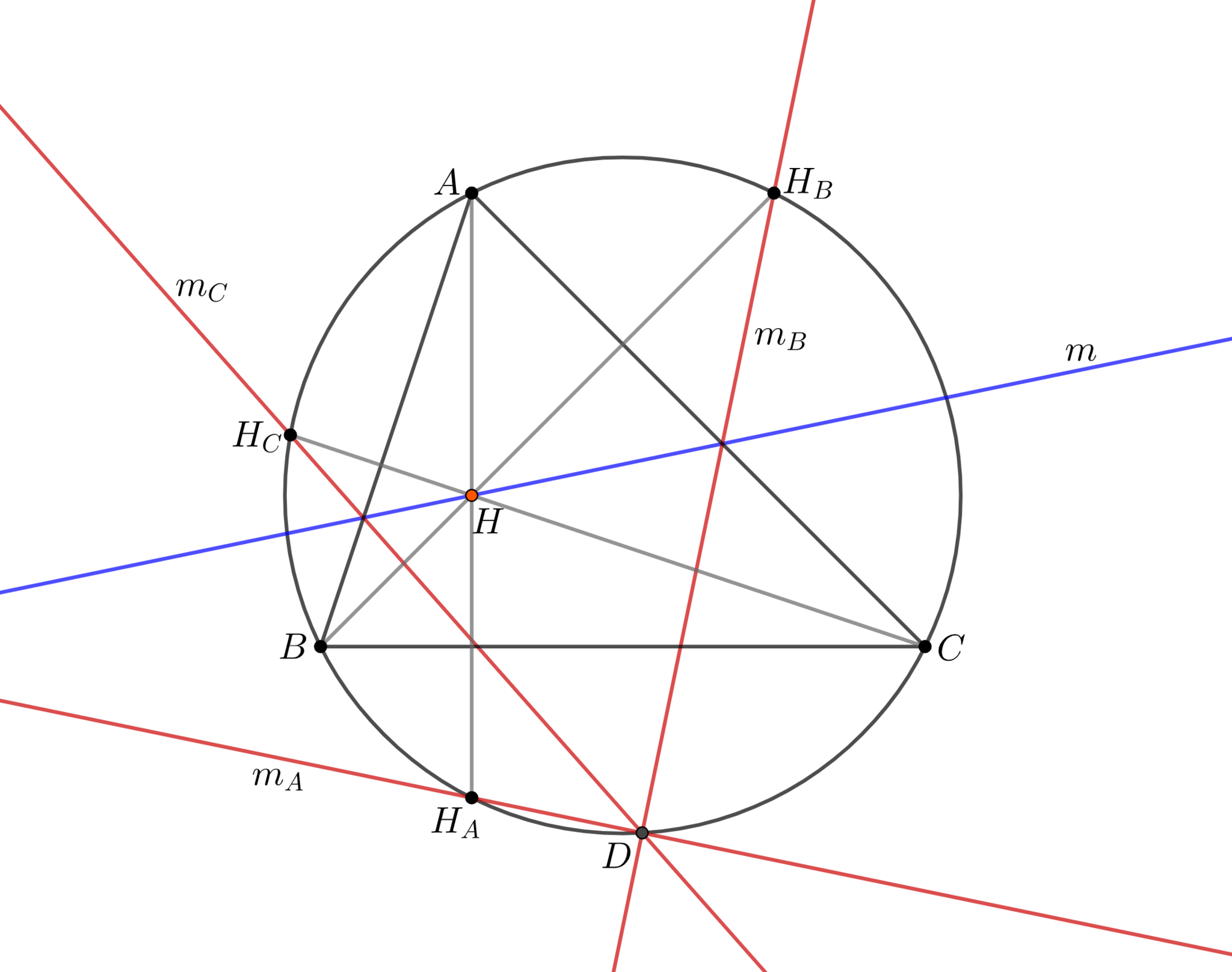反シュタイナー点

　これを使うとEGMOの問題が瞬殺できます.

EGMO2017-6

どの辺の長さも相異なる鋭角三角形 $A B C$ がある. 三角形 $A B C$ の重心 $G$ と外心 $O$ を辺 $B C, C A, A B$ に関して対称移動させた点をそれぞれ $G_{1}, G_{2}, G_{3}$ と $O_{1}, O_{2}, O_{3}$ とする. このとき, 三角形 $G_{1} G_{2} C, G_{1} G_{3} B, G_{2} G_{3} A, O_{1} O_{2} C, O_{1} O_{3} B, O_{2} O_{3} A, A B C$ の外接円は共通の点を通ることを示せ.

　反シュタイナー点についてより詳しく知りたい方はこちらの資料を参照してください.

シムソン線とミケル点

　さて, 次はミケル点の登場です.

ミケル点からの垂線の足

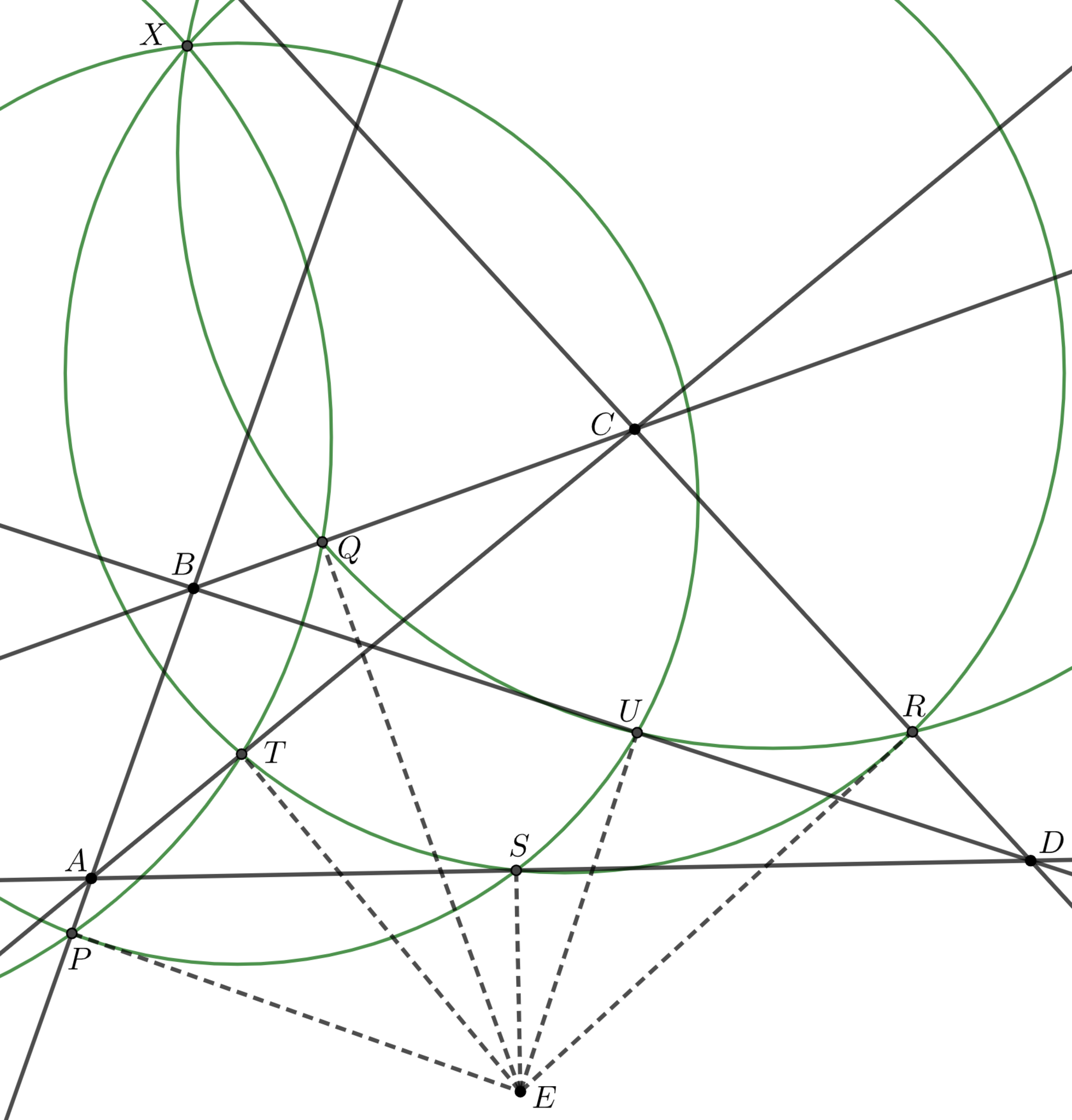
完全四辺形をなす4直線 $m_{1}, m_{2}, m_{3}, m_{4}$ があり, これらのミケル点を $M$ とする. このとき, $M$ から $m_{1}, m_{2}, m_{3}, m_{4}$ に下した垂線の足 $P_{1}, P_{2}, P_{3}, P_{4}$ は共線である.

$M$ と3直線 $m_{1}, m_{2}, m_{3}$ の作る三角形にシムソンの定理を用いて $P_{1}, P_{2}, P_{3}$ の共線がわかる. 同様の議論をもう1つの三角形に対しても行えば主張は従う.

　命題6と先ほどの命題4を合わせると, 次の定理が証明できます. これはEGMO (pp.198-200)では根軸を用いて証明されています.

ガウス・ボーデンミラーの定理

完全四辺形をなす4直線 $m_{1}, m_{2}, m_{3}, m_{4}$ がある. このとき, この4直線のうち3直線がなす三角形の垂心は4つあるが, これらは共線である.

ミケル点を $M$ とすれば, 命題6より $M$ における4つの三角形のシムソン線は一致する. よって, 命題4より従う.

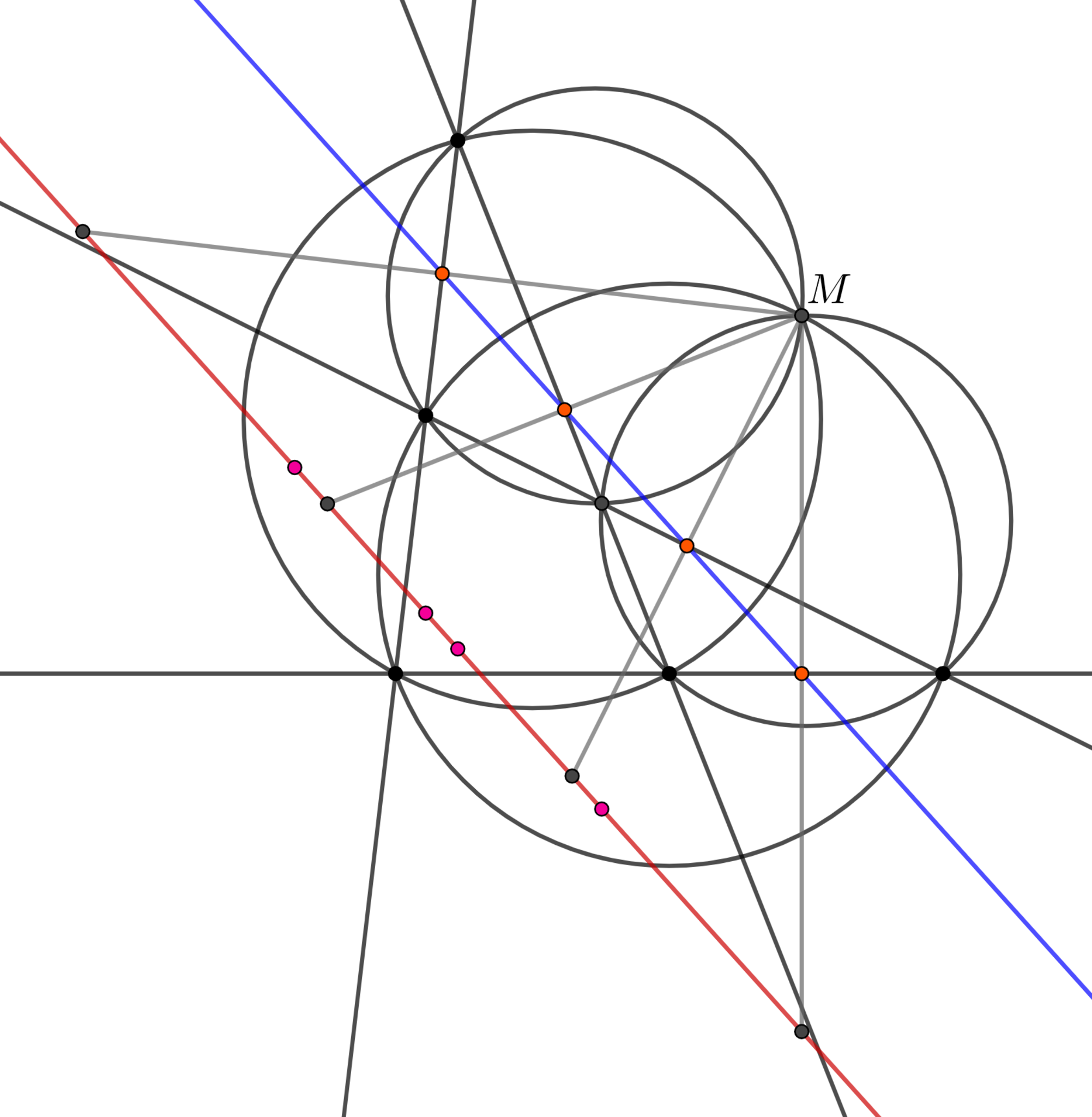ガウス・ボーデンミラーの定理

シムソン線のなす角

　2つのシムソン線がなす角は簡単に表すことができます.

シムソン線同士のなす角

三角形 $A B C$ とその外接円上の2点 $P, Q$ をとる. このとき $P, Q$ におけるシムソン線のなす角は弧 $P Q$ に対する円周角に等しい.

$P, Q$ を通り $A C$ に垂直な直線と外接円が再び交わる点を $P^{'}, Q^{'}$ とすると, 命題3より, $P, Q$ におけるシムソン線はそれぞれ $B P^{'}, B Q^{'}$ に平行である. よって, 2つのシムソン線のなす角は $∡ P^{'} B Q^{'}$ に等しく, 対称性よりこれは弧 $P Q$ の円周角に等しい.

シムソン線のなす角

　外接円の直径の両端点におけるシムソン線に関してはさらに面白い結果が知られています.

対蹠点におけるシムソン線

三角形 $A B C$ とその外接円の直径の両端点を $P, Q$ とする. このとき, $P, Q$ におけるシムソン線は $A B C$ の9点円上で直交する.

2本のシムソン線の交点を $X$ とし, $H P, H Q$ の中点をそれぞれ $M, N$ とすれば, 命題4より $M, N$ はそれぞれ $P, Q$ におけるシムソン線上にある. ここで, 命題8より $∡ N P M = 90^{\circ}$ であるから, $N M$ を直径とする円は $X$ を通る. 一方この円は $H$ を中心に外接円を1/2倍に縮小したものであるから, 9点円に一致する. 従って主張は示された.

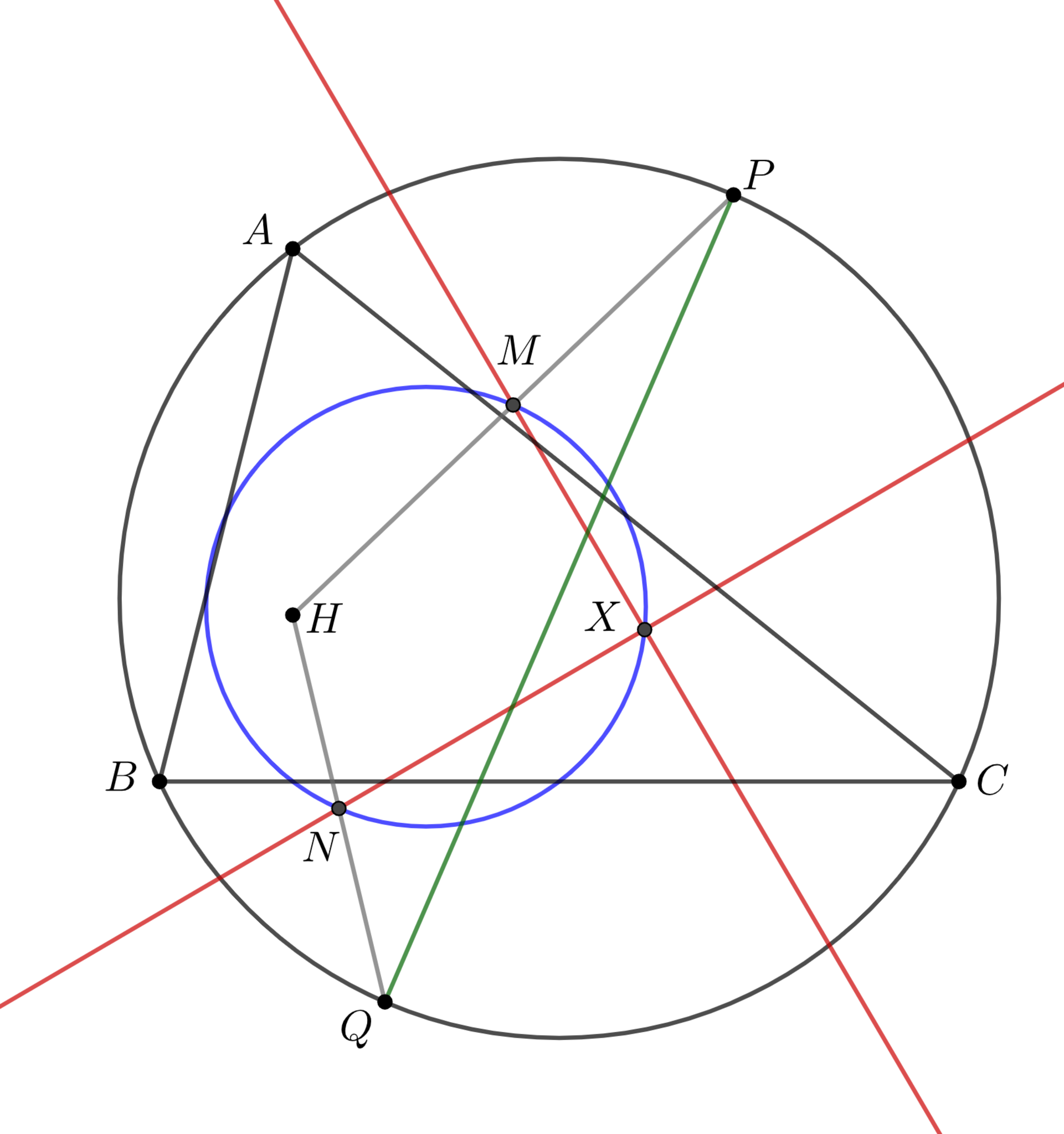対蹠点におけるシムソン線

　実はこの対蹠点におけるシムソン線が9点円上で直交するという事実は氷山の一角にすぎず, さらに強い主張が存在します. それについてはまた別の記事でいつか書こうと思いますが, 興味のある方はPoncelet pencilで調べてみてください.
　（結論から言うと, この2本のシムソン線はある直角双曲線の漸近線になっており, その双曲線はジェラベク双曲線やキーペルト双曲線などの仲間です.）

清宮の定理とターナーの定理

　シムソンの定理の拡張は, 清宮俊雄をはじめとする日本人数学者によってかなり前から研究されていました. 今回はそのうち有名な2つの結果を紹介します.

ターナーの定理

三角形 $A B C$ と点 $D$ をとり, $D$ を円 $A B C$ で反転した点を $E$ とする. $B C, C A, A B$ について $D$ と対称な点をそれぞれ $P, Q, R$ とし, $E P, E Q, E R$ が $B C, C A, A B$ と交わる点をそれぞれ $X, Y, Z$ としたとき, 3点 $X, Y, Z$ は共線である. この直線をターナー線(Turner line)という.

『シムソンの定理拡張における発想の分析』を参照.

清宮の定理

三角形 $A B C$ とその外接円上に2点 $D, E$ がある. $B C, C A, A B$ について $D$ と対称な点をそれぞれ $P, Q, R$ とし, $E P, E Q, E R$ が $B C, C A, A B$ と交わる点をそれぞれ $X, Y, Z$ としたとき, 3点 $X, Y, Z$ は共線である. この直線を清宮線(Seimiya line)という.

『シムソンの定理拡張における発想の分析』を参照.

　これらの定理については僕もあまり知らないので詳しくは言えないのですが, お気持ち的にはどちらも三角形+2点に対してシムソン線の類似物を定めているとみることができます.

シムソン線の包絡線と傍接放物線

シュタイナーデルトイド

　ある円に半径がその3分の1である円が内接しながら転がるとき, 動円の円周上の定点の軌跡をデルトイドといいます. 下の図は外接円上の点を動かしたときのシムソン線の軌跡を表示したものです. なにやらきれいな正三角形のような図形が浮かび上がっていると思いますが, これがデルトイドです.

シュタイナーデルトイド

三角形 $A B C$ の外接円上に点 $D$ を取る. $D$ が動くとき, シムソン線は常にあるデルトイドに接する. これをシュタイナーデルトイド(Steiner Deltoid)という.

数研通信の記事で初等的に証明されている.

　12/11のるささんの記事にシュタイナーデルトイドとモーリーの三角形の話が出てきて面白かったです.

シムソン線と傍接放物線

　三角形に傍接円なるものがあるじゃないですか. だったら傍接放物線があったっておかしくないですよね. （雑）

三角形 $A B C$ とその外接円上に点 $D$ をとる. このとき, $D$ を焦点とし, $D$ におけるシュタイナー線を準線とする放物線は直線 $B C, C A, A B$ に接する. この放物線を傍接放物線という.

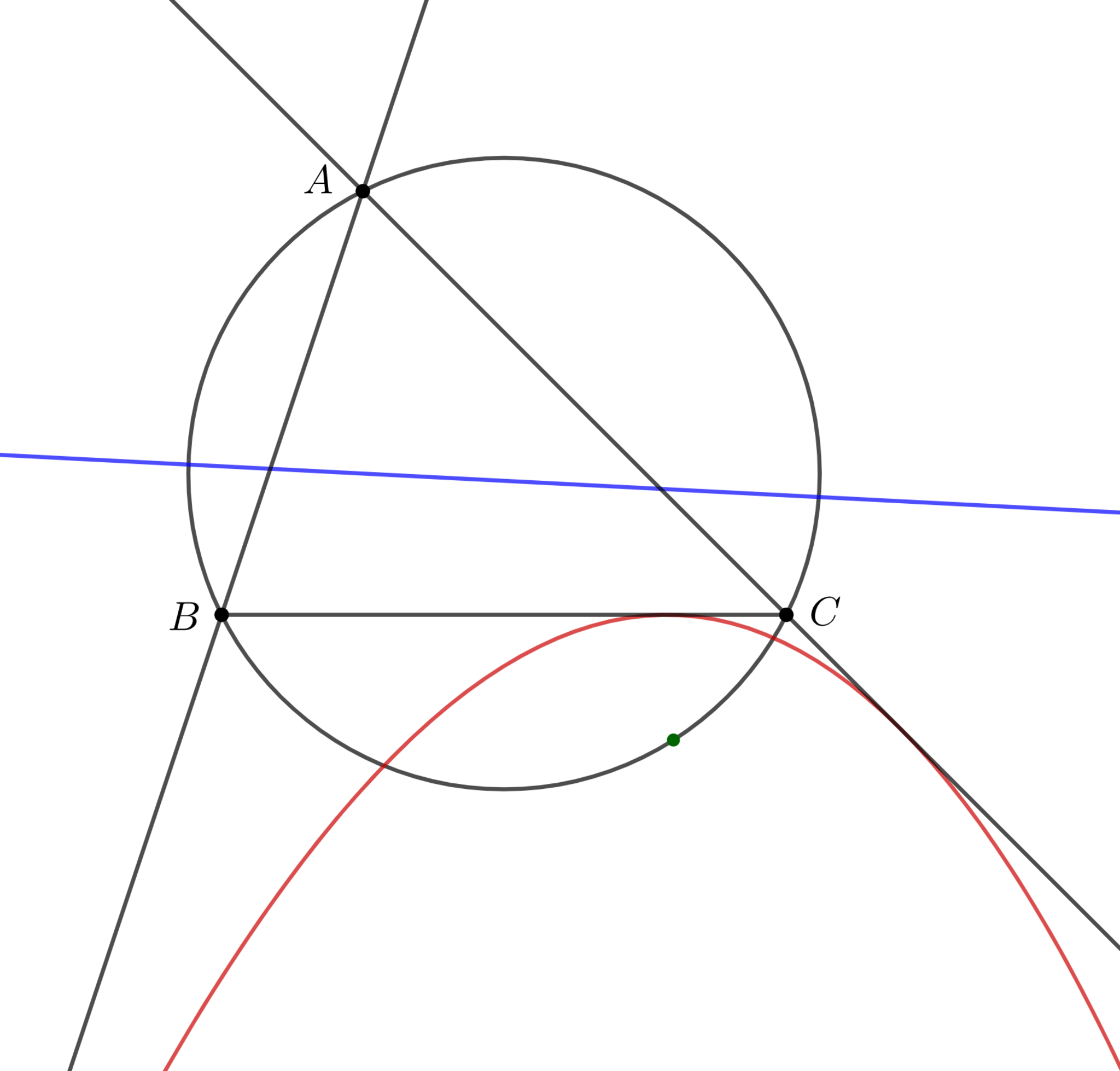傍接放物線

垂足円とオイラー・ポンスレ点

　ここまでの話では, シムソン線を「三角形とその外接円上にある点」について定まるものとして, シムソン線自体の性質をたくさん見てきました. 残る2章では, 三角形の世界を離れ, より多くの図形（例えば四角形や多角形など）にシムソン線の類似物を定めていきます.

　まず次の命題をご覧ください.

円に内接する四角形 $A B C D$ に対し, 次の8つの図形は共点である.

三角形 $B C D, C D A, D A B, A B C$ の9点円
$A, B, C, D$ における三角形 $B C D, C D A, D A B, A B C$ のシムソン線

　見た目はなんかヤバそうな感じがしますが, 丁寧にAngle-chaseをすれば簡単に示すことができます.
　実は命題12はより強い主張があり, $A B C D$ が円に内接しない場合にも成立することが知られています. しかし, 先ほど述べた通り我々はまだ三角形に対してはその外接円上の点からしかシムソン線を定義することができなかったはずです. そこで, まずは三角形と任意の点についてシムソン線の類似物を定めます.

垂足円

三角形 $A B C$ と点 $D$ に対し, $D$ から直線 $B C, C A, A B$ に下した垂線の足を通る円を垂足円(pedal circle)という.

　 $D$ が円 $A B C$ 上にあれば垂足円はシムソン線に他なりません. つまりシムソン線は半径無限大の垂足円と言えます. また, 9点円は垂心または外心における垂足円と言えます.
　このとき, 命題12でシムソン線を垂足円に置き換えた次の定理が成り立ちます.　

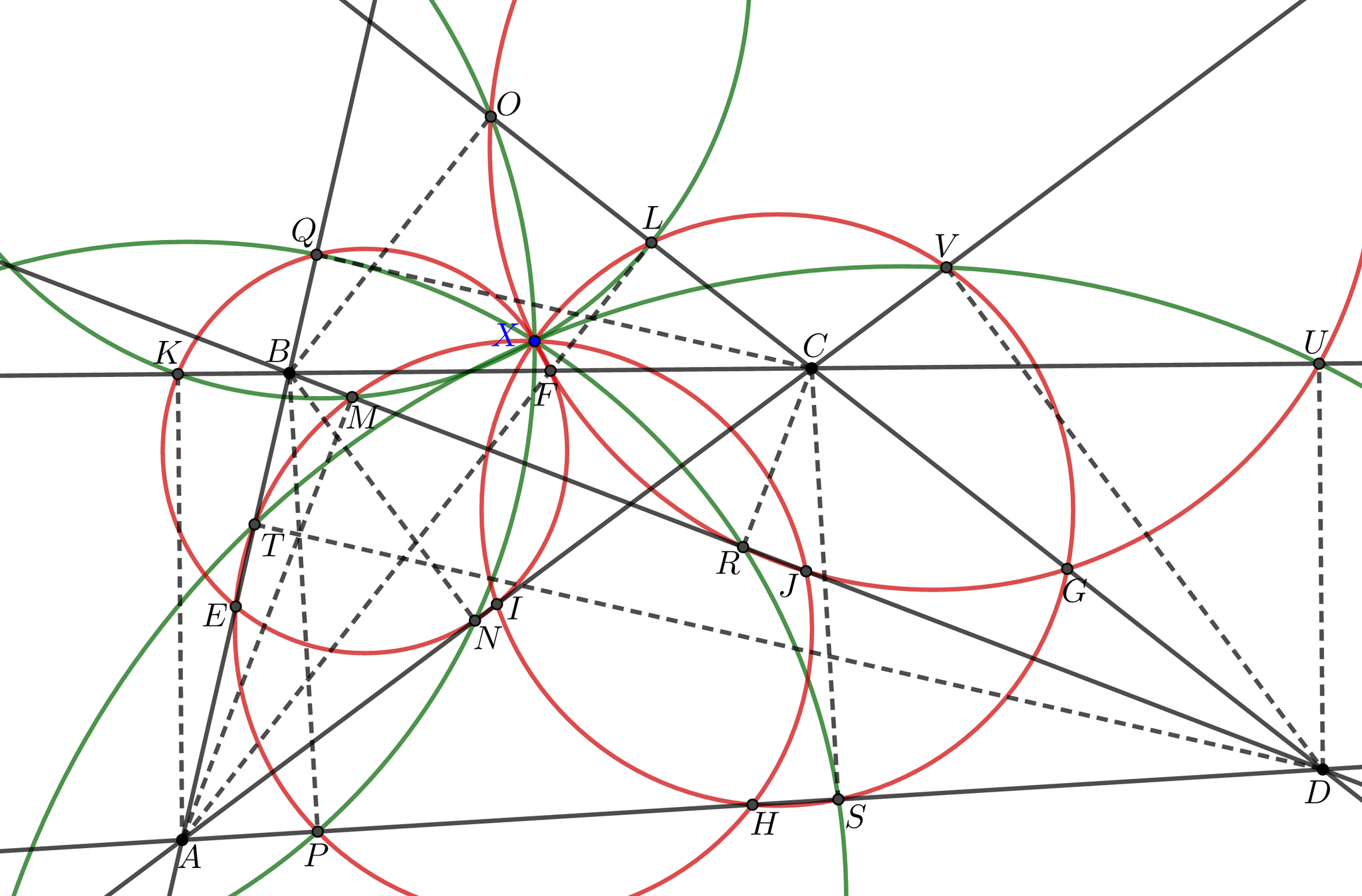
オイラー・ポンスレ点

垂心系をなさない4点 $A, B, C, D$ に対し, 次の8つの図形は共点であり, 交点をオイラー・ポンスレ点(Euler-Poncelet point)という.

三角形 $B C D, C D A, D A B, A B C$ の9点円
$A, B, C, D$ における三角形 $B C D, C D A, D A B, A B C$ の垂足円

$A B, B C, C D, D A, A C, B D$ の中点をそれぞれ $E, F, G, H, I, J$ とし, 三角形 $A B D, A C D$ の9点円の交点を $X$ とする.
$∡ E X I = ∡ E X H + ∡ H X I = ∡ E J H + ∡ H G I = ∡ H A E + ∡ I A H = ∡ I A E = ∡ E F I$
より, 4点 $E I F X$ は共円. 同様に, 4点 $G J F X$ も共円である.

$A$ から $B C, C D, D A$ に下した垂線の足を $K, L, M$ ; $B$ から $A C, C D, D A$ に下した垂線の足を $N, O, P$ ; $C$ から $A B, B D, D A$ に下した垂線の足を $Q, R, S$ ; $D$ から $A B, B C, C A$ に下した垂線の足を $T, U, V$ とすると,次を得る.
$∡ T X V = ∡ T X H + ∡ H X V = ∡ T P H + ∡ H S V = ∡ T P D + ∡ B S U = ∡ A B D + ∡ V C D$

$∡ A B D + ∡ V C D = (90^{\circ} + ∡ T D B) + (90^{\circ} + ∡ C D V) = (90^{\circ} + ∡ T U B) + (90^{\circ} + ∡ C U V)$

$(90^{\circ} + ∡ T U B) + (90^{\circ} + ∡ C U V) = ∡ T U B + ∡ C U D = ∡ T U B + ∡ B V U = ∡ T U V$

よって, 4点 $T U V X$ は共円である. 他の3組についても同様に示される.

オイラー・ポンスレ点

　オイラー・ポンスレ点は垂足円の応用事例として「こんなのがあるよ」という紹介にとどめてもよかったのですが, それだとシムソンの定理と同じく「ふ～ん」となって終わりかねないので, せっかくなのでオイラー・ポンスレ点に関する面白い事実を1つ紹介します.

補足:オイラー・ポンスレ点と直角双曲線

　漸近線が直交する双曲線を直角双曲線といいます. 直角双曲線は初等幾何と円錐曲線のつながりにおいてとても重要で, 代表的な双曲線であるジェラベク双曲線, キーペルト双曲線, フォイエルバッハ双曲線などはすべて直角双曲線です. これらの双曲線はいずれも三角形の五心やオイラー線に関わるものですが, 実はオイラー・ポンスレ点と直角双曲線も密接に関係しています.

直角双曲線と垂心

3点 $A, B, C$ を通る双曲線 $H$ に対し, 以下は同値である.

直角双曲線である
三角形 $A B C$ の垂心を通る.

本質でないので省略. 幾何教程(下)(pp.298-299)ではパスカルの定理を用いて証明されている.

　4点 $A, B, C, D$ が垂心系(orthocentric system)をなすとは, $D$ が三角形 $A B C$ の垂心であることを指します.

オイラー・ポンスレ点は直角双曲線の中心

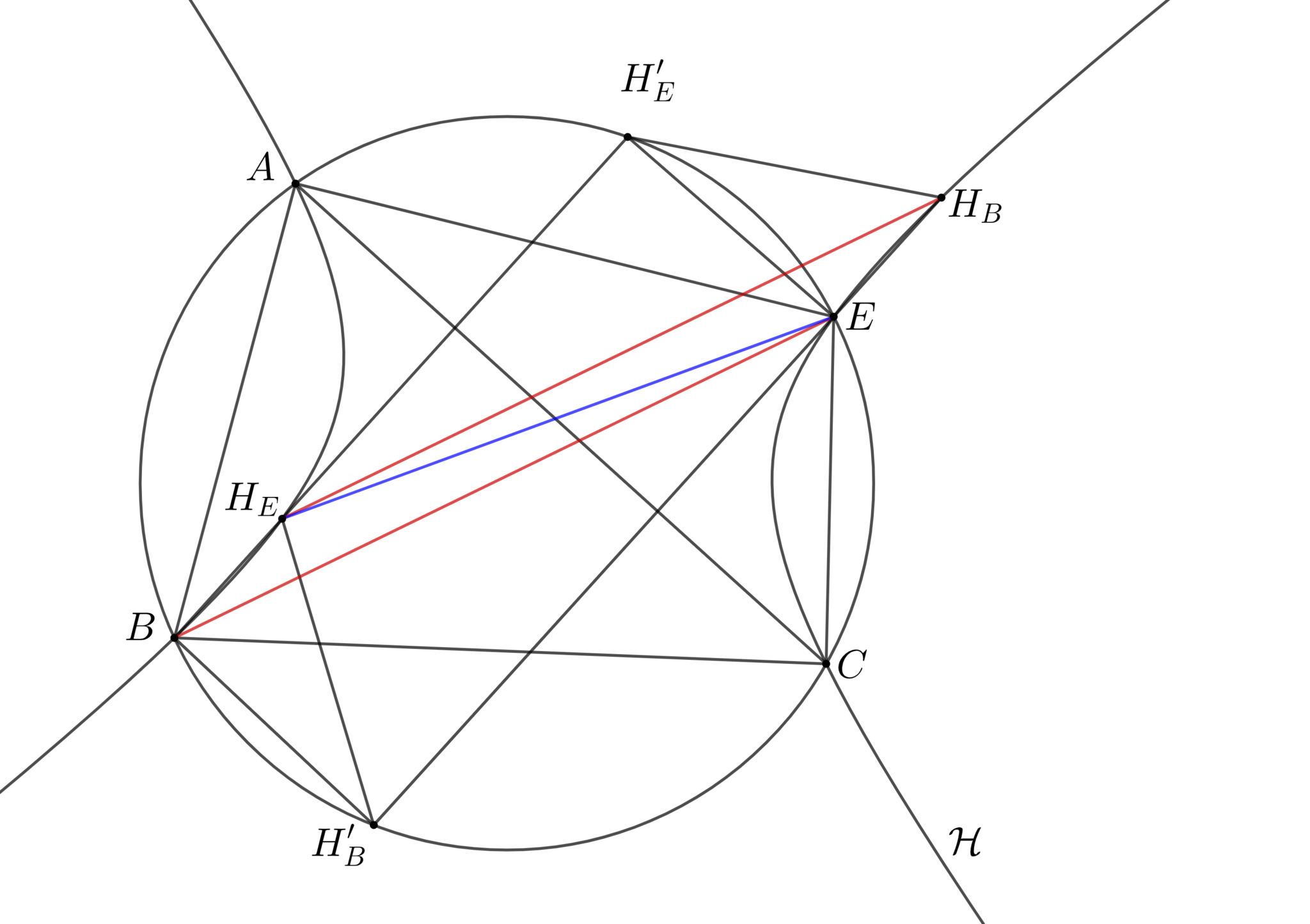
垂心系をなさない4点 $A, B, C, D$ に対し, $A, B, C, D$ を通る直角双曲線の中心はオイラー・ポンスレ点に一致する.

$H$ の中心が三角形 $A B C$ の9点円上にあることを示す.
$H$ と円 $A B C$ が再び交わる点を $E$ , 三角形 $A B C$ の垂心を $H_{E}$ , 三角形 $A C E$ の垂心を $H_{B}$ とし, $B H_{E}, E H_{B}$ と円 $A B C$ が再び交わる点をそれぞれ $H_{E}^{'}, H_{B}^{'}$ とする.
簡単な角度計算より, $A C$ は $H_{E} H_{E}^{'}, H_{B} H_{B}^{'}$ の垂直二等分線であるから, $H_{E} H_{E}^{'} H_{B} H_{B}^{'}$ は等脚台形である.
一方, $B H_{E}^{'} E H_{B}^{'}$ も等脚台形であるから, 三角形 $H_{E}^{'} E H_{B}$ と三角形 $H_{E}^{'} B H_{B}$ は合同である. よって $B H_{E} H_{B} E$ は平行四辺形であるから, $H$ の中心は $H_{B} E$ の中点であり, これは9点円上にある.

同様にして $H$ の中心は三角形 $B C D, C D A, D A B$ の9点円上にあることが示せるから, オイラー・ポンスレ点に一致する.

$\mathcal{H}の中心はオイラー・ポンスレ点$ \mathcal{H}の中心はオイラー・ポンスレ点

　これを使うとこんなことが示せます.

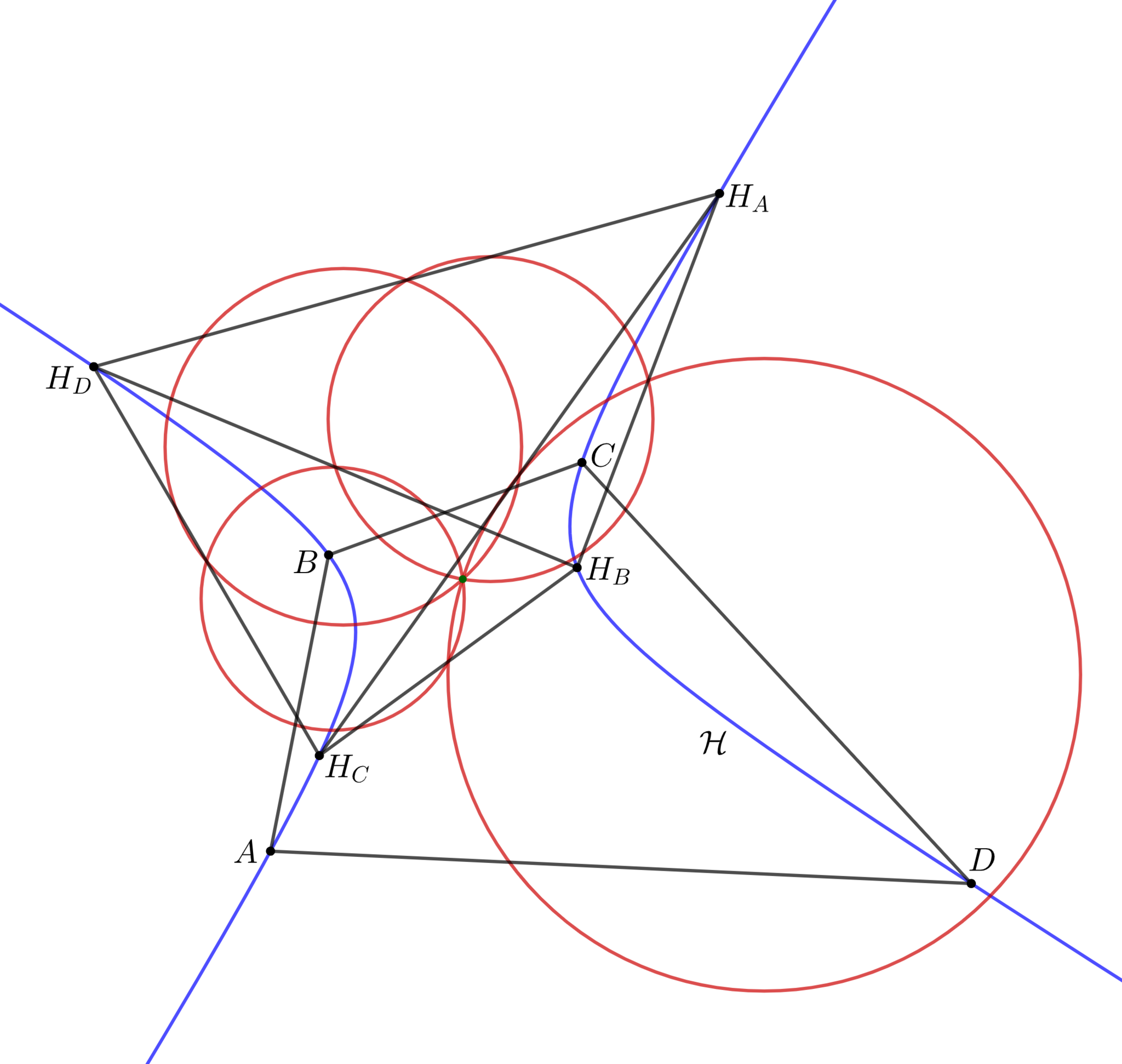
垂心系をなさない4点 $A, B, C, D$ に対し, 三角形 $B C D, C D A, D A B, A B C$ の垂心をそれぞれ $H_{A}, H_{B}, H_{C}, H_{D}$ とすると, $A, B, C, D$ のオイラー・ポンスレ点と $H_{A}, H_{B}, H_{C}, H_{D}$ のオイラー・ポンスレ点は一致する.

4点 $A, B, C, D$ を通る直角双曲線 $H$ をとれば, 補題14よりこれは $H_{A}, H_{B}, H_{C}, H_{D}$ を通る. よって, 2つのオイラー・ポンスレ点は $H$ の中心に他ならない.

オイラー・ポンスレ点の一致

　4点をそれぞれの垂心に置き換えることでオイラー・ポンスレ点を共有する4点の組が次々と作られるの, 面白いですよね. さらに, 命題16において $A B C D$ が共円の時, 四角形 $A B C D$ と $H_{A} H_{B} H_{C} H_{D}$ は合同になります. これの証明は皆さんに投げておきます

四角形に対するシムソン線・垂足円

　最後にシムソン線を四角形, 多角形の世界まで広げていきます.

四角形に対するシムソン線

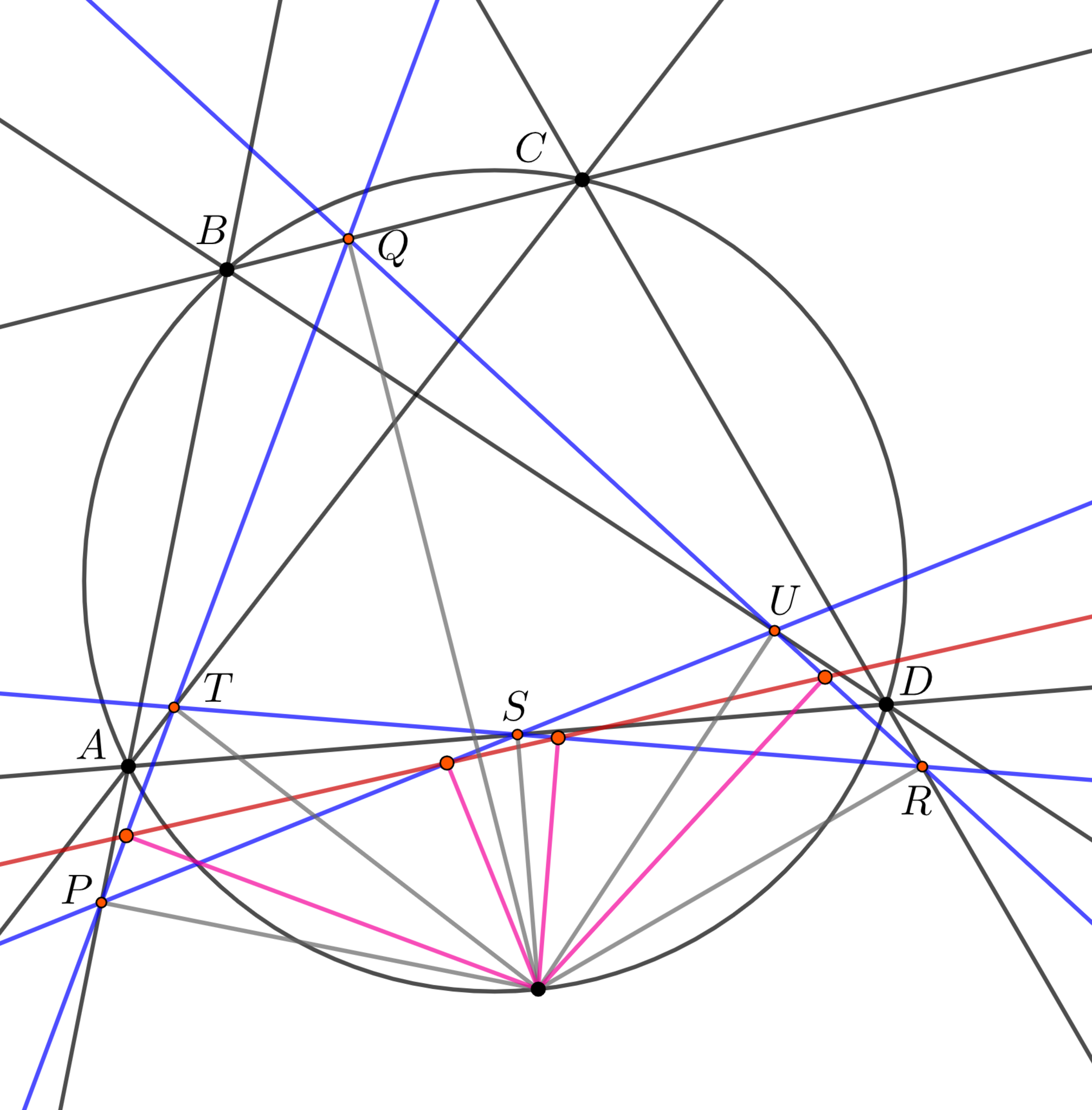
円に内接する四角形 $A B C D$ とその外接円上に点 $E$ をとる. このとき, $E$ における三角形 $B C D, C D A, D A B, A B C$ のシムソン線に $E$ から下した垂線の足は共線である. この4点を通る直線を $E$ における $A B C D$ のシムソン線とする.

$M$ から $A B, B C, C D, D A, A C, B D$ に下した垂線の足をそれぞれ $P, Q, R, S, T, U$ とすると, $A M P S T, B M P Q U, C M Q R T, D M R S U$ はすべて共円である. よって, $E$ は4本のシムソン線がつくる完全四辺形のミケル点に他ならない. よって命題6より主張は従う.

四角形のシムソン線

　私はこの事実をこのサイトで知りました. 証明が載っていなかったので自分で示しましたが, ミケル点からの垂線の足の構図に帰着されるのは面白いです.
　そして五角形やそれ以上の多角形の場合もミケル点からの垂線の足による議論でこの命題が成立することが示せるはずです.

円に内接する $N$ 角形 $A_{1} A_{2} \dots A_{N}$ とその外接円上の点 $B$ に対し, $B$ における「 $N$ 点 $A_{1}, A_{2}, \dots A_{N}$ から $N - 1$ 点を選んでできる $N$ 個の $N - 1$ 角形」のシムソン線に $B$ から下した垂線の足は共線である. この $N$ 点を通る直線を $B$ における $A_{1} A_{2} \dots A_{N}$ のシムソン線とする.

　さて, ひとつ前の章で垂足円を導入したときと同じように, 「外接円上の点」にしか定義されないという制約はなくしたいわけです. そこで, 円に内接するとは限らない四角形に対し, 任意の点における垂足円を定義します.
　命題17において, シムソン線を垂足円に置き換えればうまくいきそうな感じがしますが, 1つ問題があります. 命題17をそのまま拡張すると, 4つの垂足円に $E$ から下した「垂線の足」が共円, みたいなことが言えたらうれしいのですが, 「円に垂線を下す」というところが意味不明ですね.
　しかし, 実はこの場合4つの垂足円は本質的に4直線, つまりシムソン線と変わりません. その理由となるのが次の補題です.

四角形 $A B C D$ と点 $E$ について, $E$ における三角形 $B C D, C D A, D A B, A B C$ の垂足円は共点である.

$E$ から $A B, B C, C D, D A, A C, B D$ に下した垂線の足をそれぞれ $P, Q, R, S, T, U$ とし,垂足円 $P T Q, Q R U$ の交点を $O$ とする.
このとき, 5点 $A E P S T, B E P Q U, C E Q R T, D E R S U$ はそれぞれ共円である. よって, 次のように計算できるので, 4点 $R T S O$ は共円である.
$∡ T O R = ∡ T O Q + ∡ Q O R = ∡ T O Q + ∡ Q U R = ∡ T P Q + ∡ Q U B + ∡ D U R = ∡ T P Q + ∡ Q P B + ∡ D S R = ∡ T P A + ∡ D S R = ∡ T S A + ∡ D S R = ∡ T S R$

同様にして, 4点 $P U S O$ の共円も示されるから主張は従う.

（下の図で $O$ に相当するところが $X$ と書かれています. 申し訳ありません.）
垂足円の束

　実は補題20はミケルの定理の特殊な場合に他なりません.

ミケルの四辺形定理（反転形）

1点 $O$ で交わる4円 $C_{i} (i = 1, 2, 3, 4)$ をとり. 各 $i, j$ に対し $C_{i}, C_{j}$ の $O$ 以外の交点を $V_{i j}$ とする. このとき, 4円 $V_{12} V_{23} V_{31}, V_{23} V_{34} V_{42}, V_{34} V_{41} V_{13}, V_{41} V_{12} V_{24}$ は共点である. この交点を4円 $C_{i} (i = 1, 2, 3, 4)$ のミケル点とする.

$O$ を中心に反転すれば通常のミケルの四辺形定理に帰着される.

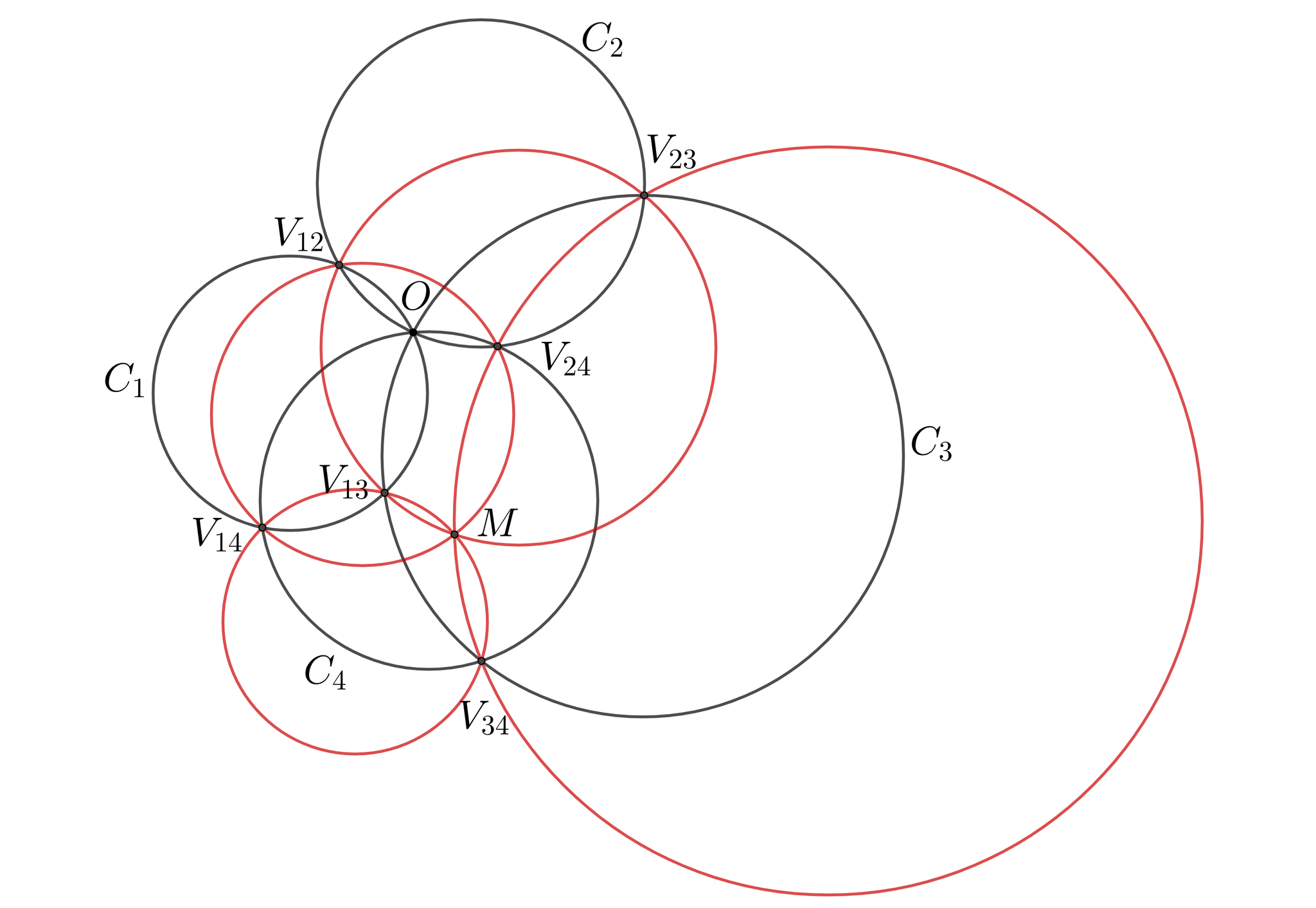反転されたミケル点

　「一般の位置にある4直線」と「1点を共有する4円」は本質的にほとんど同じとみなせます. なぜなら4円を共有点を中心に反転すれば4直線に移るからです. 従って, 次のようにすれば四角形の垂足円が定義できます.

四角形の垂足円

四角形 $A B C D$ と点 $E$ をとる. $E$ における三角形 $B C D, C D A, D A B, A B C$ の垂足円を $C_{A}, C_{B}, C_{C}, C_{D}$ とし, 各 $i = A, B, C, D$ について $E$ を通り $C_{i}$ に直交する円が $C_{i}$ と再び交わる点を $H_{i}$ とする. このとき, $H_{A} H_{B} H_{C} H_{D}$ は共円である. この4点を通る円を $E$ における $A B C D$ の垂足円とする.